线性规划问题

一、线性规划问题及其标准型

1.问题的求解过程



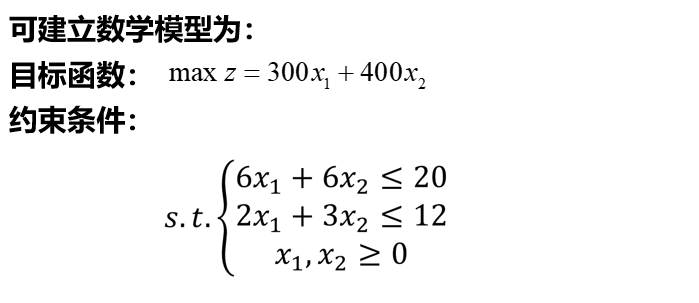
2.标准形式

二、非标准形问题的转换

三、线性规划问题中的Matlab求解

四、案例分析

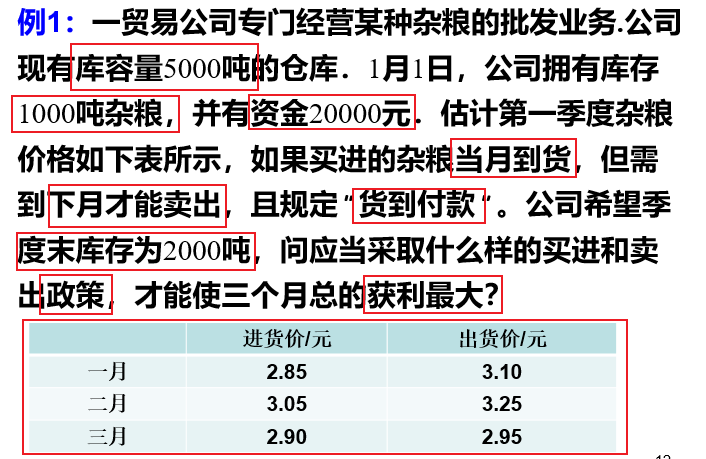
问题分析

分析结果



整理出表达式

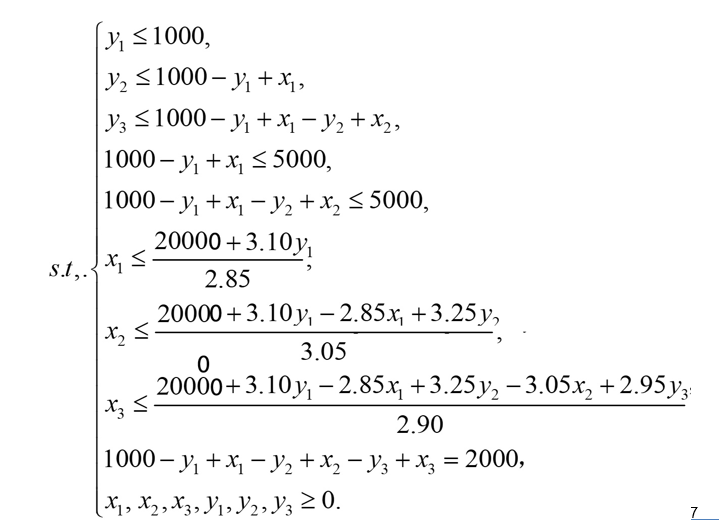
代码实现
可以把下面代码，先存到M文件，然后运行，也可以逐行粘贴至命令行运行

f=[-2.85,-3.05,-2.9,3.1,3.25,2.95];
f=f';f=-f;%价值向量，并转化为求最小值时对应的价值向量
A=[0,0,0,1,0,0;
  -1,0,0,1,1,0;
  -1,-1,0,1,1,1;
  1,0,0,-1,0,0;
 1,1,0,-1,-1,0;
 2.85,0,0,-3.1,0,0;
 2.85,3.05,0,-3.1,-3.25,0;
 2.85,3.05,2.9,-3.1,-3.25,-2.95];
b=[1000;1000;1000;4000;4000;20000;20000;20000];%线性不等式约束
aeq=[1,1,1,-1,-1,-1];beq=1000;%线性等式约束
lb=zeros(6,1);%函数值下限
[x,y]=linprog(f,A,b,aeq,beq,lb);%输出x中后三项分别代表y1,y2,y3
 x=reshape(x,1,6),-y%重新组合矩阵x，取负求得原本的最大值

运行结果如下：

五、蒙特卡洛相关方法的介绍

x=unifrnd(0,12,[1,10000000]);
y=unifrnd(0,9,[1,10000000]);
Pinshu=sum(y<x.^2&x<=3)+sum(y<12-x&x>=3);
Area_appr=12*9*Pinshu/10^7

%运行结果在49.5附近，由于是随机模拟，因此每次的结果都是不一样的。

最后

以上就是慈祥抽屉最近收集整理的关于Matlab——线性规划模型线性规划问题的全部内容，更多相关Matlab——线性规划模型线性规划问题内容请搜索靠谱客的其他文章。