概述
本文已整合到这里：Python内置数学模块全整理，易查易阅
文章目录
- 基本原理
- 整数和字节
- 分布函数
- 用于序列的随机函数
基本原理
用于生成伪随机数，之所以有个伪字，是因为计算机没法生成真正的随机数。所谓伪随机数，无非是把一个初始值变得面目全非，从而很像随机数。
而这个初始值，便是通过seed实现的，如果不设置，则默认为当前的系统时间。
在ramdom中，使用最多的应该就是random.random()了，其功能为返回一个
[
0
,
1
)
[0,1)
[0,1)区间的实数。接下来可以通过random.random()来验证以下random.seed()的功能。
>>> def rand(n):
... random.seed(n)
... print(random.random())
... print(random.random())
...
>>> rand(3)
0.23796462709189137
0.5442292252959519
>>> rand(3)
0.23796462709189137
0.5442292252959519
使用seed的一个好处是方便算法复现，比如用某个随机数做算法，然后换了个随机数之后发现算法不对了，这个时候非常尴尬，这个时候seed就派上了用场。
相比之下，getstate和setstate更加强大，可以获取或设置当前的状态。
>>> a = random.getstate()
>>> random.random()
0.36995516654807925
>>> random.random()
0.6039200385961945
>>> random.setstate(a)
>>> random.random()
0.36995516654807925
>>> random.random()
0.6039200385961945
整数和字节
接下来的所有代码默认from random import *。
randbytes(n) | 生成n个字节 |
randrange(b) | 生成一个[0,b]之间的整数 |
randrange(a,b,step=1) | 在range(a,b,step)中随机选一个数 |
randint(a,b) | 相当于randrange(a, b+1) |
getrandbits(k) | 相当于randint(0,2**k) |
分布函数
random中的分布函数均为浮点型。
| 分布函数 f ( x ) f(x) f(x) | ||
|---|---|---|
uniform(a,b) | [a,b]间均匀分布 | 1 ∣ b − a ∣ , x ∈ [ a , b ] frac{1}{|b-a|}, xin[a,b] ∣b−a∣1,x∈[a,b] |
triangular(a,b,mid) | 三角分布 | |
betavariate(a,b) | β beta β分布 | Γ ( a + b ) Γ ( a ) Γ ( b ) x a − 1 ( 1 − x ) b − 1 frac{Gamma(a+b)}{Gamma(a)Gamma(b)}x^{a-1}(1-x)^{b-1} Γ(a)Γ(b)Γ(a+b)xa−1(1−x)b−1 |
expovariate(a) | 指数分布 | a ⋅ e − a x x > 0 acdot e^{-ax}quad x>0 a⋅e−axx>0 |
gammavariate(a,b) | γ gamma γ分布 | x a − 1 exp ( − x b ) Γ ( a ) ∗ b a frac{x^{a-1}exp(frac{-x}{b})}{Gamma(a)*b^a} Γ(a)∗baxa−1exp(b−x) |
gauss(b,c) | 正态分布 | 1 2 π c exp ( x − b ) 2 2 c 2 frac{1}{sqrt{2pi}c}expfrac{(x-b)^2}{2c^2} 2πc1exp2c2(x−b)2 |
normalvariate(b,c) | 正态分布，慢于gauss | 1 2 π c exp ( x − b ) 2 2 c 2 frac{1}{sqrt{2pi}c}expfrac{(x-b)^2}{2c^2} 2πc1exp2c2(x−b)2 |
lognormvariate(b,c) | 对数正态分布 | 1 c x 2 π exp ( ln x − b ) 2 2 c 2 frac{1}{cxsqrt{2pi}}expfrac{(ln x-b)^2}{2c^2} cx2π1exp2c2(lnx−b)2 |
vonmisesvariate(a,b) | 冯·米塞斯分布 | exp [ b cos ( x − a ) 2 π J 0 ( b ) ] exp[frac{bcos(x-a)}{2pi J_0(b)}] exp[2πJ0(b)bcos(x−a)] |
paretovariate(a) | 帕累托分布 | x − a x^{-a} x−a |
weibullvariate(a,b) | 韦伯分布 | b a ( x a ) b − 1 exp [ − ( x a ) b ] frac{b}{a}(frac{x}{a})^{b-1}exp[-(frac{x}{a})^b] ab(ax)b−1exp[−(ax)b] |
注：
Γ ( x ) = ∫ 0 + ∞ t z − 1 e − t d t ( x > 0 ) Gamma(x)=int^{+infty}_0t^{z-1}e^{-t}text dtquad(x>0) Γ(x)=∫0+∞tz−1e−tdt(x>0)
J 0 ( x ) = ∑ m = 0 ∞ ( − 1 ) m m ! Γ ( m + 1 ) ( x 2 ) 2 m J_0(x)=sum_{m=0}^inftyfrac{(-1)^m}{m!Gamma(m+1)}(frac{x}{2})^{2m} J0(x)=∑m=0∞m!Γ(m+1)(−1)m(2x)2m
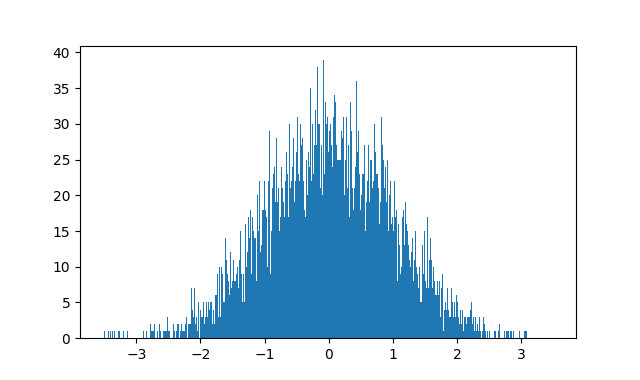
通过matplotlib可绘制一下分布的形状，以正态分布为例：
import matplotlib.pyplot as plt
xs = [gauss(0,1) for _ in range(10000)]
plt.hist(xs,1000)
plt.show()
用于序列的随机函数
choice(lst)：从lst中随机选择一个数shuffle(lst)：把lst打乱sample(lst, k, counts=None)：从lst中选出k个数，counts代表lst中对应元素的个数，为整数。
choices(lst，weights=None, cum_weights=None, k=1)：从lst中选择一个子列表
- k为元素个数
- weights为相对权重数组，长度与lst相同，每个元素都大于0，代表对应元素出现的概率权重，
- cum_weights为累加权重数组，长度与lst相同
最后
以上就是瘦瘦小鸭子为你收集整理的python伪随机数模块random详解的全部内容，希望文章能够帮你解决python伪随机数模块random详解所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复