连续时间基本信号
信号与系统课程涉及的连续时间基本信号主要包含:普通信号(连续时间复指数信号、采样信号),奇异信号(单位阶跃信号、单位斜坡信号、单位冲激信号),常用信号(门信号、符号信号、三角信号)。
一、普通信号
(一)连续时间复指数信号
x
(
t
)
=
e
s
t
,
−
∞
<
t
<
∞
x(t) = e^{st}, quad -infty<t<infty
x(t)=est,−∞<t<∞
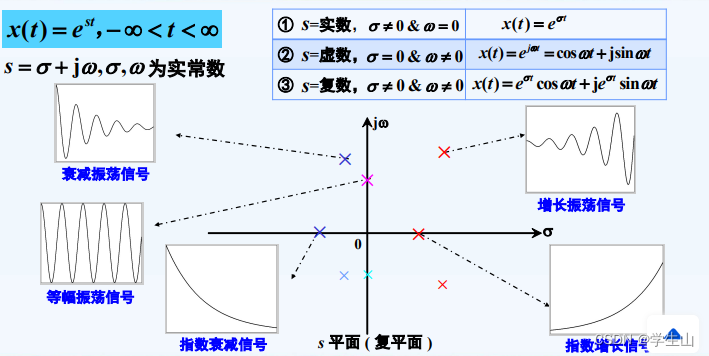
(二)采样信号
S
a
(
t
)
=
s
i
n
t
t
Sa(t) = {sint over t}
Sa(t)=tsint
后续学习主要会使用到的性质:
-
e v e n . even. even.
-
t = k π , S a ( t ) = 0 , ∣ k ∣ ≥ 1 t = kpi,Sa(t) = 0,{lvert k rvert}geq 1 t=kπ,Sa(t)=0,∣k∣≥1.
-
l i m t → 0 S a ( t ) = 1 lim_{trightarrow0}Sa(t) = 1 limt→0Sa(t)=1.
-
∫ − ∞ ∞ S a ( t ) d t = π Large{int_{-infty}^{infty}Sa(t)dt = pi} ∫−∞∞Sa(t)dt=π.
二、奇异信号
(一)单位阶跃信号
后续学习主要会使用到的性质:
1.单边特性:
y
(
t
)
=
x
(
t
)
u
(
t
)
y(t) = x(t)u(t)
y(t)=x(t)u(t)
示意如图:
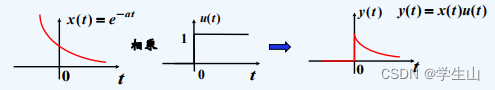
- 表示信号的作用区间: x ( t ) = ( 2 − t ) ( u ( t ) − u ( t − 2 ) ) x(t) = (2-t)(u(t)-u(t-2)) x(t)=(2−t)(u(t)−u(t−2))
(二)单位斜坡信号
存在和单位阶跃信号的微积分转化关系: d d t r ( t ) = u ( t ) ∫ − ∞ t u ( τ ) d τ = r ( t ) = t u ( t ) begin{aligned} {d over dt}r(t) &= u(t) \ int_{-infty}^{t}u(tau)dtau &= r(t) = tu(t)end{aligned} dtdr(t)∫−∞tu(τ)dτ=u(t)=r(t)=tu(t)
(三)单位冲激信号
1.筛选特性,筛选出
t
0
t_0
t0:
x
(
t
)
δ
(
t
−
t
0
)
=
x
(
t
0
)
δ
(
t
−
t
0
)
begin{aligned}x(t)delta(t - t_0) &= x(t_0)delta(t-t_0)end{aligned}
x(t)δ(t−t0)=x(t0)δ(t−t0)
2. 取样特性,在积分限内就取得到
t
0
t_0
t0时的样:
∫
−
∞
∞
x
(
t
)
δ
(
t
−
t
0
)
d
t
=
x
(
t
0
)
int_{-infty}^{infty}x(t)delta(t-t_0)dt = x(t_0)
∫−∞∞x(t)δ(t−t0)dt=x(t0)
3. 展缩特性,提取系数:
δ
(
a
t
+
b
)
=
1
a
δ
(
t
+
b
a
)
delta(at+b) = {1over a}delta(t+{b over a})
δ(at+b)=a1δ(t+ab)
P
S
:
PS:
PS:由
a
=
−
1
,
b
=
0
⟹
δ
(
−
t
)
=
δ
(
t
)
a = -1, b = 0impliesdelta(-t) = delta(t)
a=−1,b=0⟹δ(−t)=δ(t), 偶函数。
4. 复合函数性质:
δ
[
s
i
n
(
t
)
]
=
∑
k
=
−
∞
∞
δ
(
t
−
k
π
)
delta[sin(t)] = sum_{k = -infty}^{infty}delta(t - kpi)
δ[sin(t)]=k=−∞∑∞δ(t−kπ)
若
x
(
t
)
=
0
x(t) = 0
x(t)=0有
n
n
n个互不相等的实根
t
1
,
t
2
,
⋯
,
t
n
t_1, t_2, cdots, t_n
t1,t2,⋯,tn,则:
δ
[
x
(
t
)
]
=
∑
i
=
1
n
1
∣
x
′
(
t
i
)
∣
δ
(
t
−
t
i
)
{delta[x(t)] = sum_{i = 1}^{n}{1 over {lvert x'(t_i) rvert}}delta(t-t_i)}
δ[x(t)]=i=1∑n∣x′(ti)∣1δ(t−ti)
存在和单位阶跃信号的微积分转化关系: ∫ − ∞ t δ ( τ ) d τ = u ( t ) d d t u ( t ) = δ ( t ) begin{aligned} int_{-infty}^{t}delta(tau)dtau= u(t)\{dover dt}u(t) = delta(t) end{aligned} ∫−∞tδ(τ)dτ=u(t)dtdu(t)=δ(t)
三、常用信号
(一)门信号
x
(
t
)
=
(
2
−
t
)
[
u
(
t
)
−
u
(
t
−
2
)
]
x
(
t
)
=
(
2
−
t
)
G
2
(
t
−
1
)
begin{aligned} x(t)&=(2-t)[u(t) - u(t-2)]\ x(t)&=(2-t)G_2(t-1)end{aligned}
x(t)x(t)=(2−t)[u(t)−u(t−2)]=(2−t)G2(t−1)
G
τ
(
t
)
G_tau(t)
Gτ(t)图像如下图所示,形似一道门。
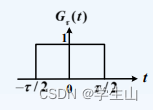
(二)三角信号
Λ
2
τ
(
t
)
=
{
1
−
∣
t
∣
τ
∣
t
∣
≤
τ
0
∣
t
∣
>
τ
Lambda_{2tau}(t)=left{begin{aligned} 1-{{lvert trvert}over tau}quad &lvert trvert leq tau \ 0 quad &lvert trvert >tauend{aligned}right.
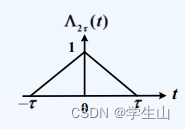
Λ2τ(t)=⎩
⎨
⎧1−τ∣t∣0∣t∣≤τ∣t∣>τ
三角信号的一种表示形式,今后会学习更为便利的表示方式,暂作了解即可。
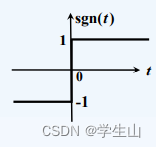
(三)符号信号
工程意义很大的经典信号。
s
g
n
(
t
)
{
1
t
>
0
−
1
t
<
0
sgn(t)left{begin{aligned} 1 quad t>0 \ -1 quad t<0 end{aligned}right.
sgn(t){1t>0−1t<0
最后
以上就是积极纸飞机最近收集整理的关于信号系统_连续时间基本信号连续时间基本信号的全部内容,更多相关信号系统_连续时间基本信号连续时间基本信号内容请搜索靠谱客的其他文章。








发表评论 取消回复