本篇博文是看完西安电子科技大学的魏青老师的课程所做的学习笔记,特此记录。
文章目录
- 雷达方程
- 最小可检测信号
- 脉冲积累对作用距离的改善
- 目标截面积及其起伏特性
- 系统损耗
- 传播过程中各种因素的影响
- 雷达方程的几种形式
雷达方程
- 基本雷达方程
理想、无损耗、自由空间传播的单基地雷达方程

由于接收到的功率Pr必须超过最小可检测的信号功率Simin,雷达才能可靠地发现目标,当Pr=Simin时,就课得到雷达检测该目标的最大作用距离Rmax- 当收发天线不共用的时:
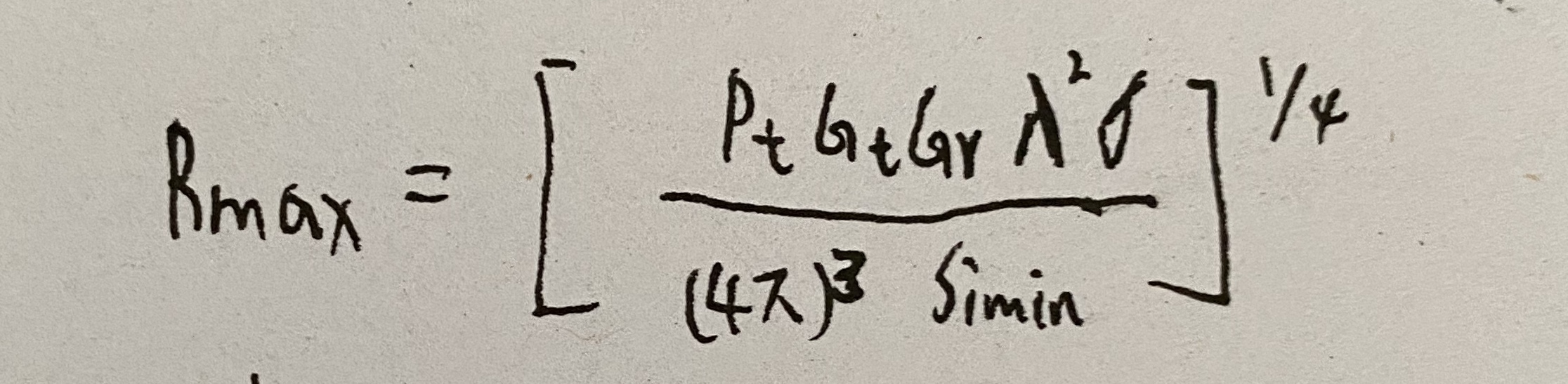
- 当收发天线公用时:
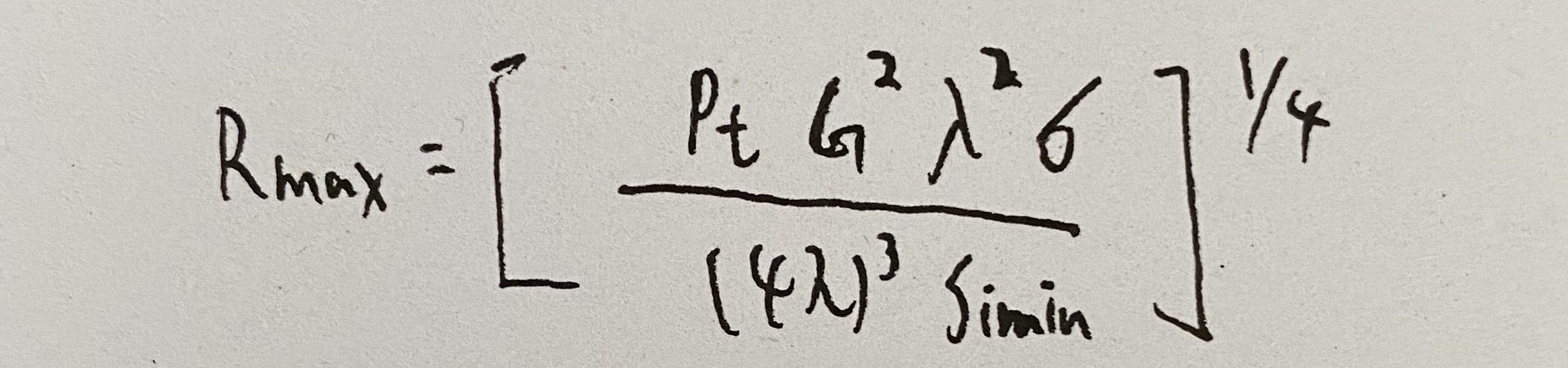
雷达的作用距离不是一个确定的值,而是统计值,对于一个雷达来说,不能简单地说它的作用距离是多少,通常是在概率的意义上讲,当虚警概率Pfa(10-6)和发现概率Pd(90%)给定时的作用距离是多大
- 当收发天线不共用的时:
- 目标的雷达截面积
- 定义:

P2为目标散射的总功率,S1为照射的功率密度
由于二次散射,因而在雷达接收点处单位立体教内的散射功率为
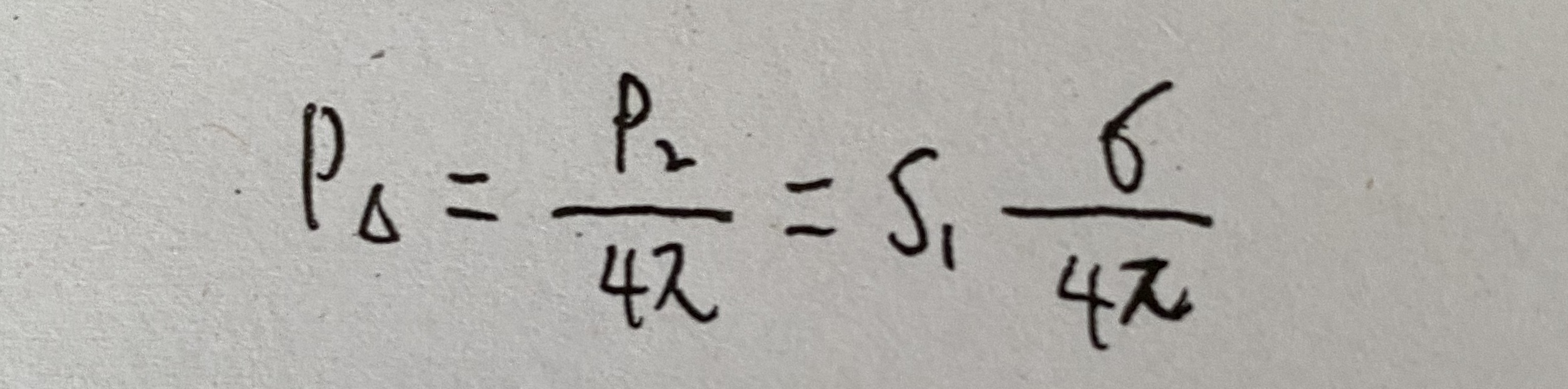 因此雷达的截面积又可定义为
因此雷达的截面积又可定义为
- 定义:
最小可检测信号
-
最小可检测信号与信噪比
最小可检测信号:
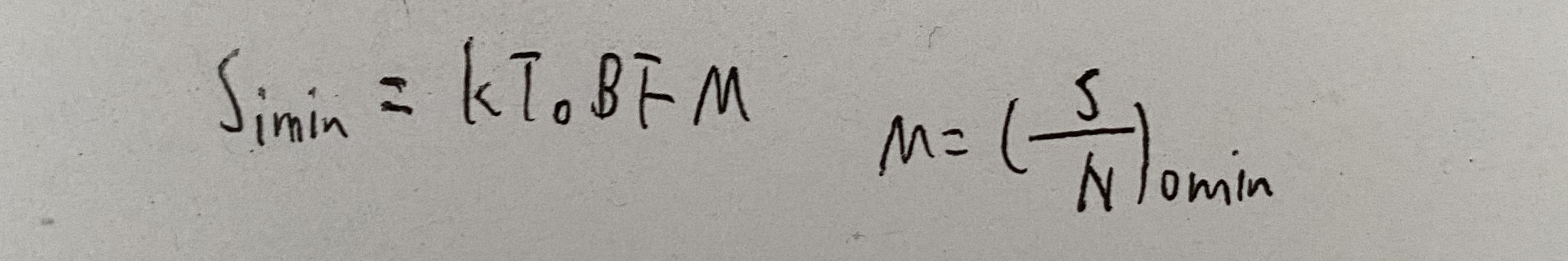
在早期的雷达中,通常都用各类显示器来观察和检测目标信号,所以成M为识别系数。而多数现代雷达则采用建立在统计理论基础上的统计判决方法来实现信号检测,在这种情况下,检测目标信号所需的最小输出信噪比称为检测因子(Detectability Factor)D0。
D0是在需要满足所需检测性能(以检测概率Pd和虚警概率Pfa表征),在接收机匹配滤波器输出端(检波器输入端)单个脉冲需要达到的最小信号噪声功率比。 -
门限检测
奈曼-皮尔逊准则,要求在给定信噪比的条件下,满足一定虚警概率Pfa时的发现概率Pd最大
门限检测是一种统计检测,由于信号叠加有噪声,因而总输出是一个随机量。在输出端根据输出振幅是否超过门限来判断有无目标存在,分为以下4种情况:- 存在目标时判为有目标,这是一种正确的判断,称为发现,它的概率称为发现概率Pd
- 存在目标时判为无目标,这是错误判断,称为漏报,它的概率称为漏报概率Pla
- 不存在目标时判为无目标,称为正确不发现,它的概率称为正确不发现概率Pan
- 不存在目标时判为有目标,称为虚警,这是一种错误判断,它的概率称为虚警概率Pfa
四种概率的关系:
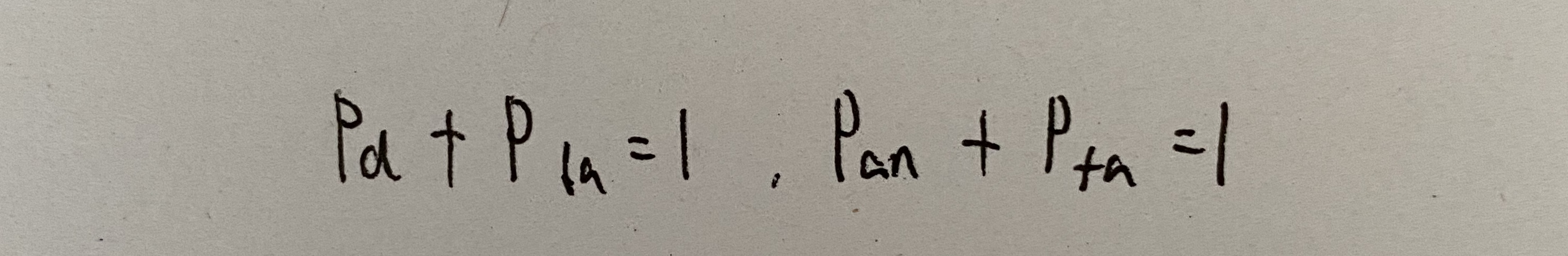
-
检测性能和信噪比
- 虚警概率
虚警是指没有信号而仅有噪声,噪声电平超过门限值被误认为信号的事件。噪声超过门限的概率称为虚警概率。
虚警概率Pfa:
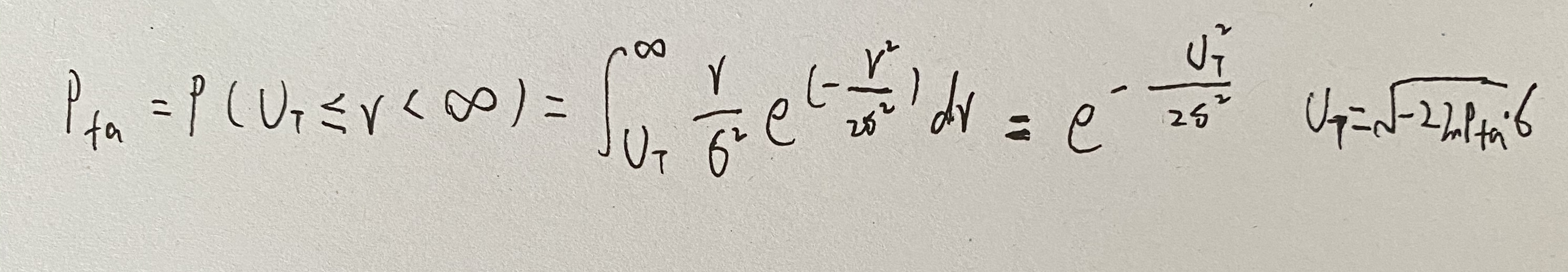
下图说明了虚警概率与门限电平的关系:
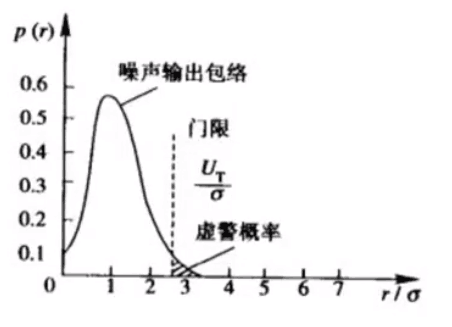
当噪声分布函数一定时,虚警的大小完全取决于门限电平。
下图说明额虚警时间和虚警概率
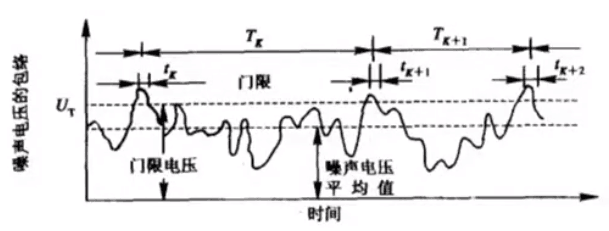
虚警概率Pfa可以近似包络实际超过门限的总时间与观察时间的比值来得到:
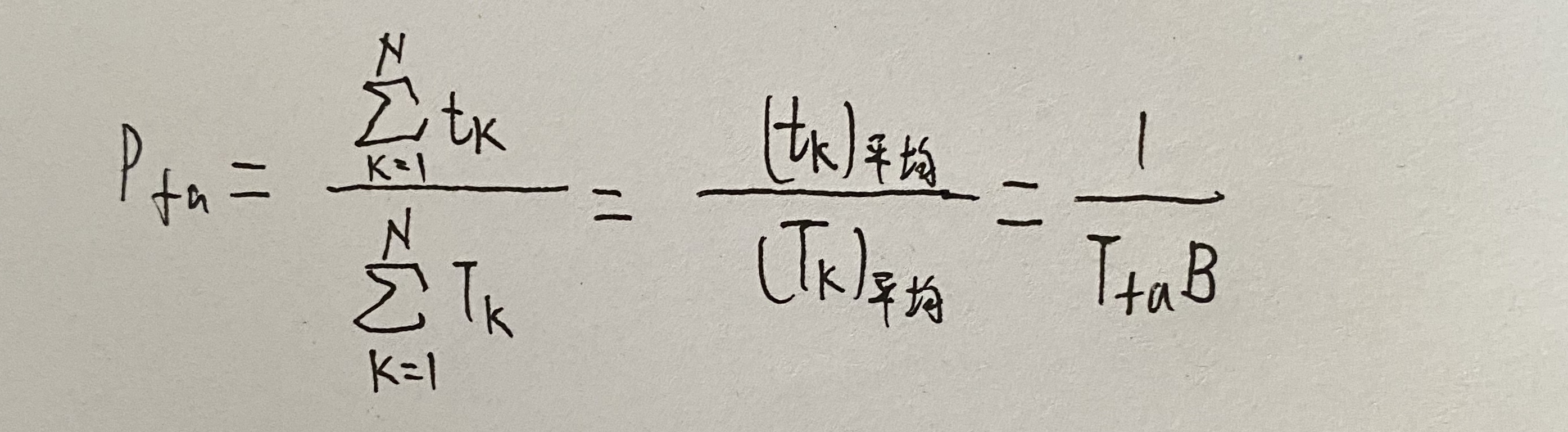
虚警宽度tk = 1/B,虚警时间Tfa
虚警总数是虚警概率的倒数
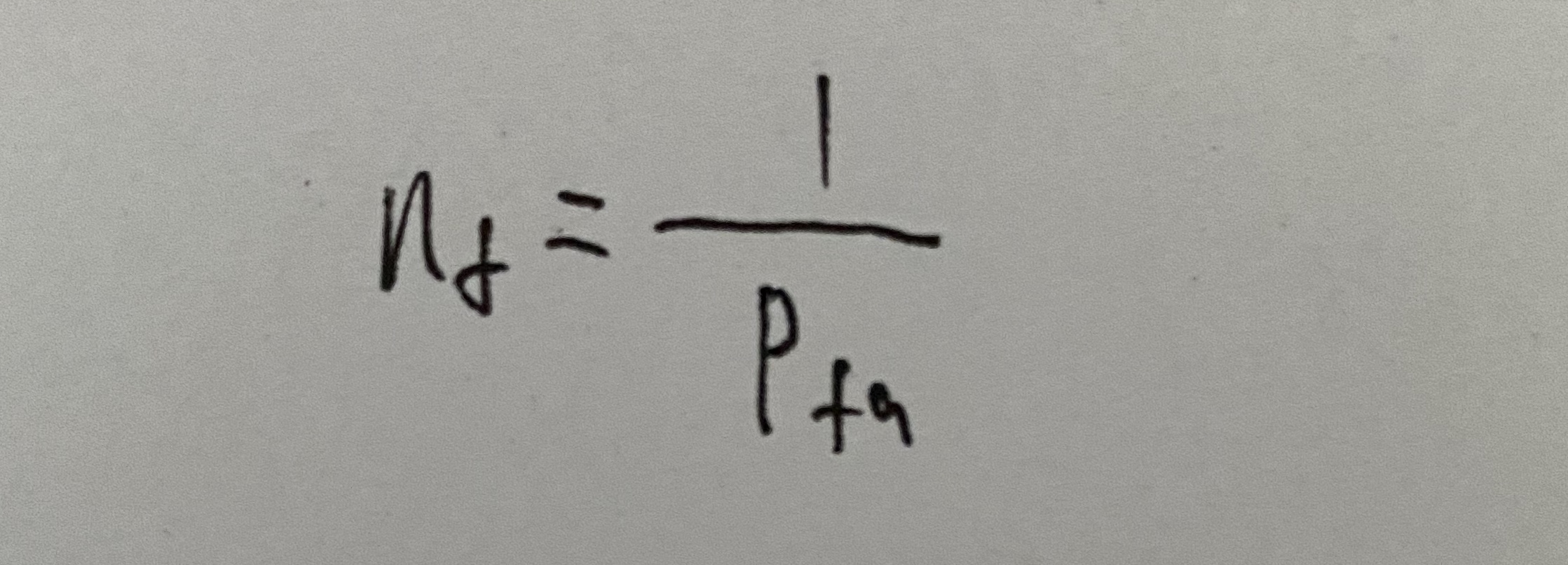
- 发现概率
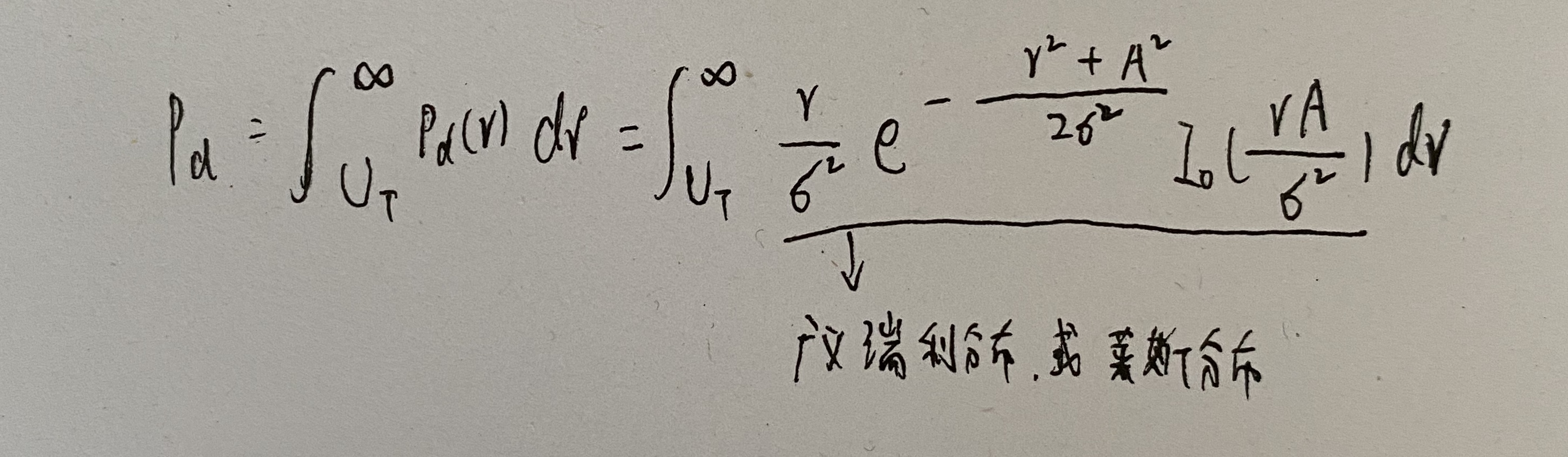
非起伏目标单个脉冲线性检波时检测概率和所需信噪比(检测因子)的关系曲线
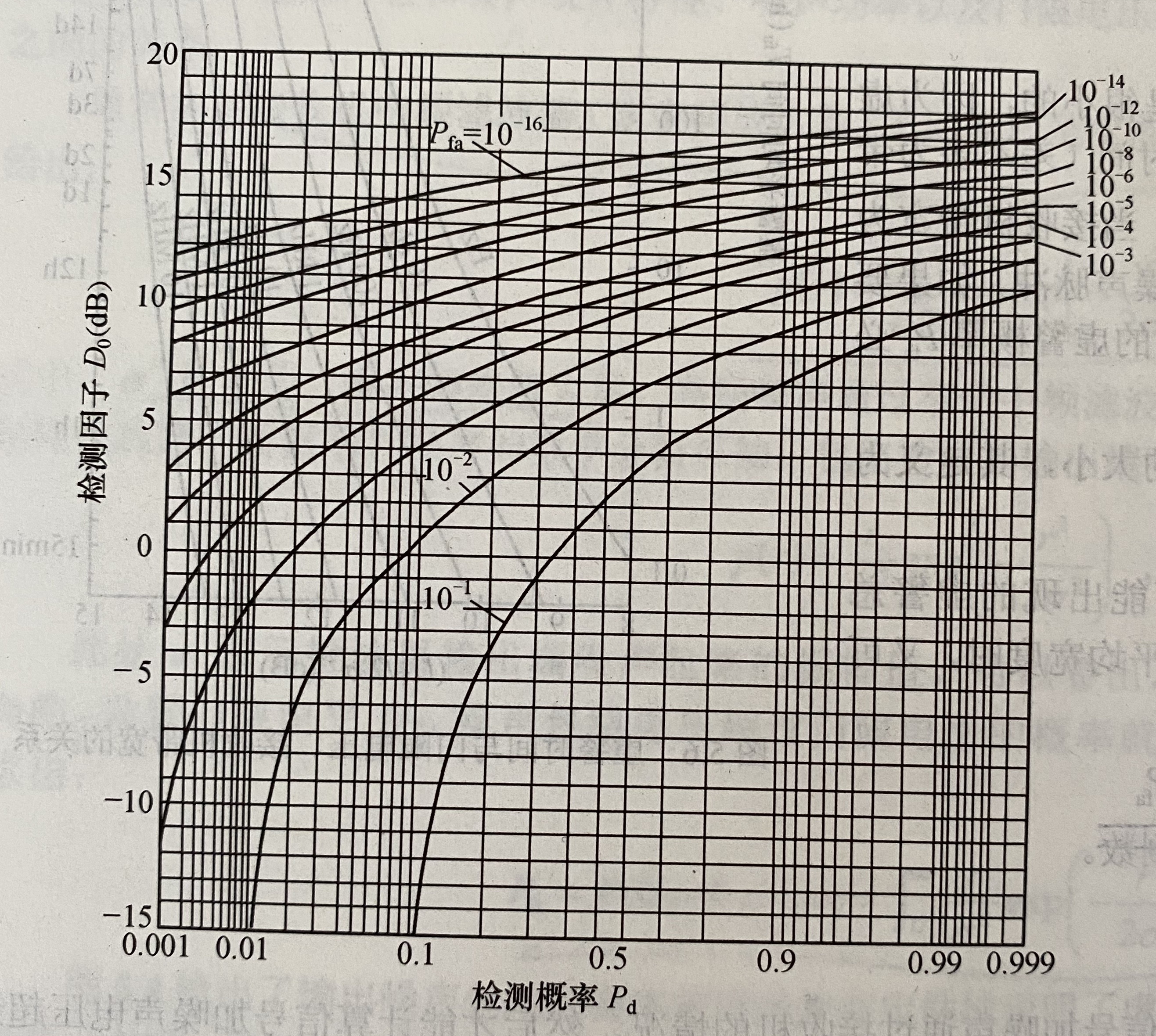
当虚警概率一定时,信噪比越大,发现概率越大,也就是说,门限电平一定时,发现概率随信噪比的增大而增大
- 虚警概率
脉冲积累对作用距离的改善
多个脉冲积累后可以有效地提高信噪比,从而改善雷达地检测能力
- 相参积累
信号在中频积累时要求信号间有严格地相位关系,即信号是相参的。
将M个等幅相参中频信号进行相参积累,可以使信噪比(S/N)提高为原来的M倍(M为积累脉冲数)。
对于理想的相参积累,M个等幅脉冲积累后对检测因子D0的影响是:
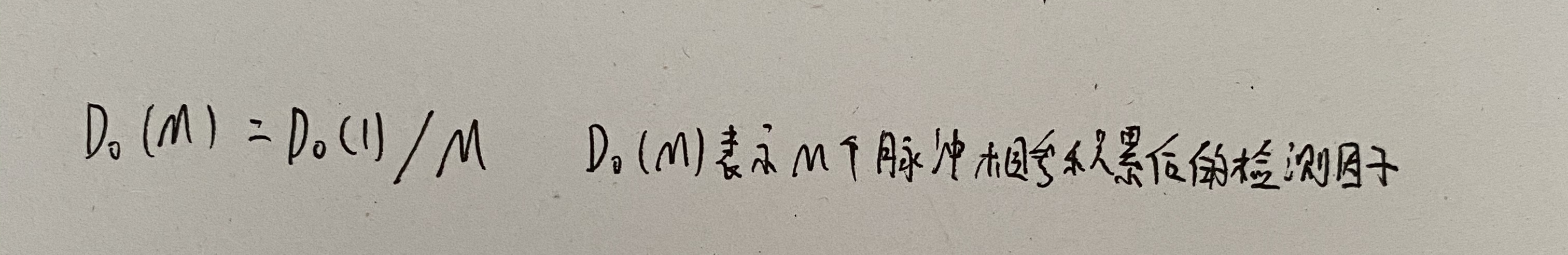
因为这种积累使信噪比提高为原来的M倍,所以在门限检测前达到相同信噪比时,检波器输入端所要求的单个脉冲信噪比D0(M)将减小到不积累时的D0(1)的1/M。
最大作用距离的变化:
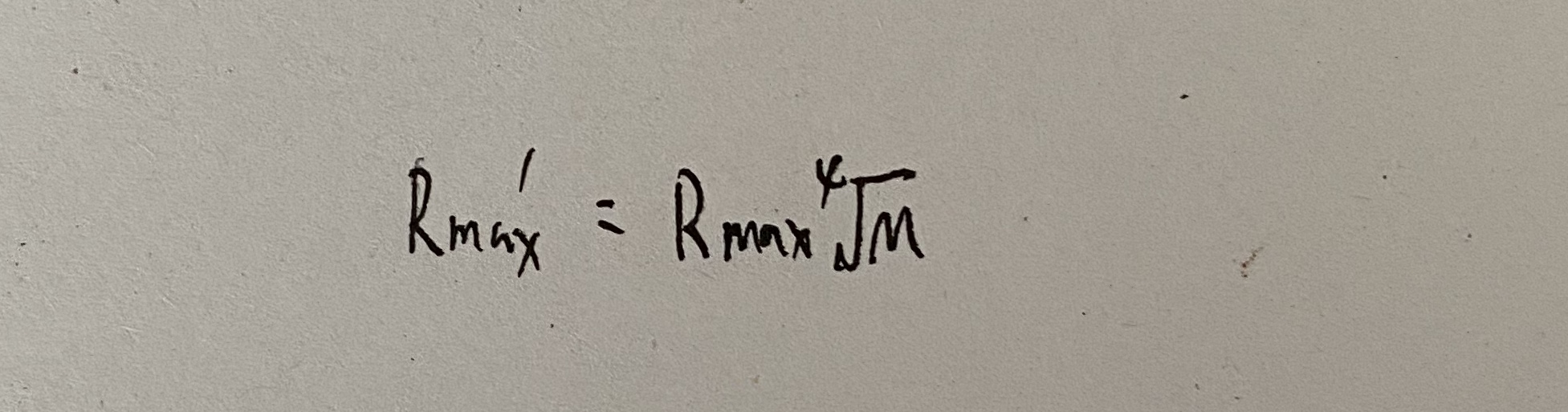
- 非相参积累
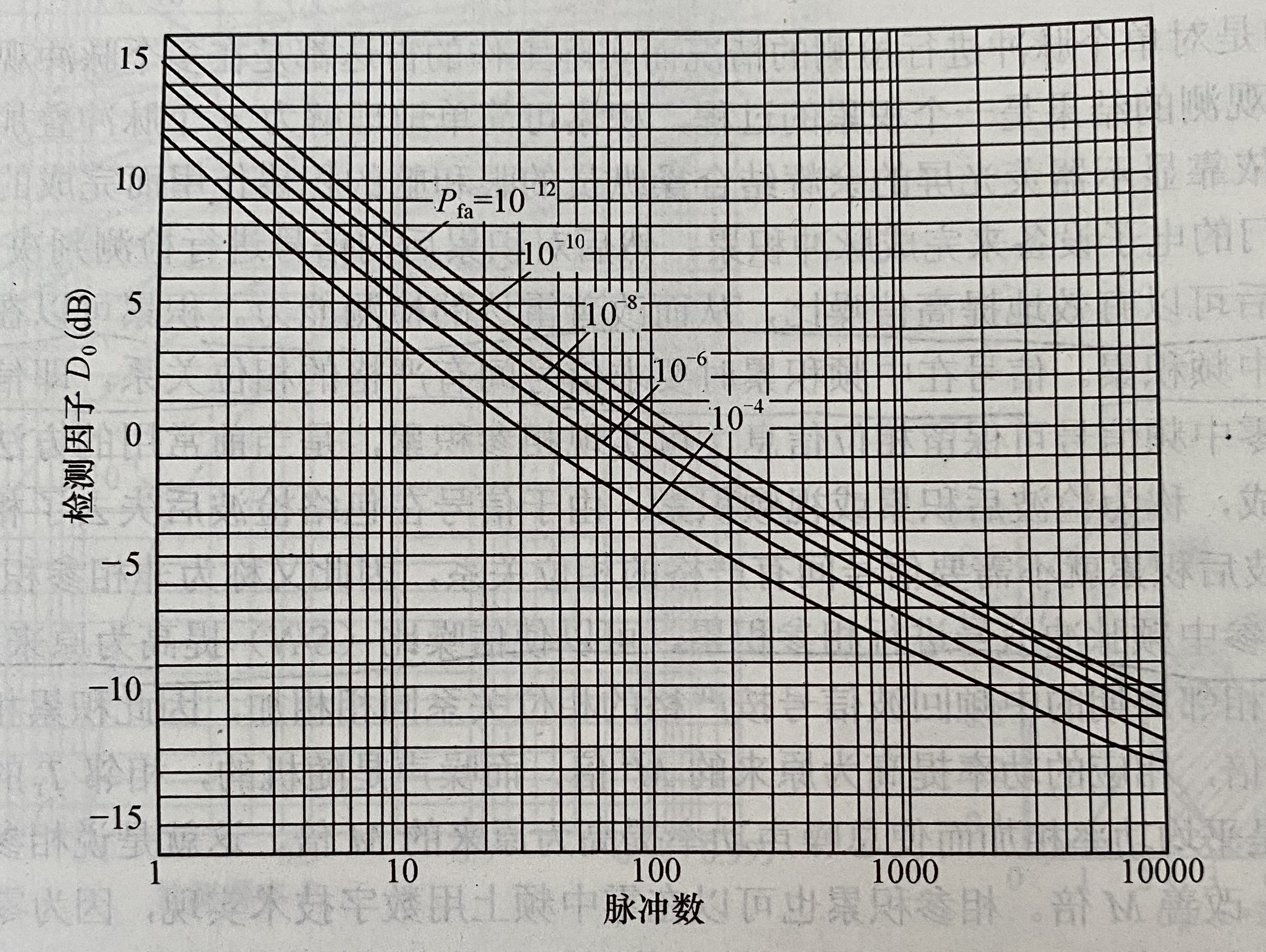
非相参积累数的确定是通过查下面的两个图:- 线性检波非起伏目标检测因子(所需信噪比)与非相参脉冲积累数的关系,Pd=0.5
- 线性检波非起伏目标检测因子与非相参脉冲积累数的关系,Pd=0.9
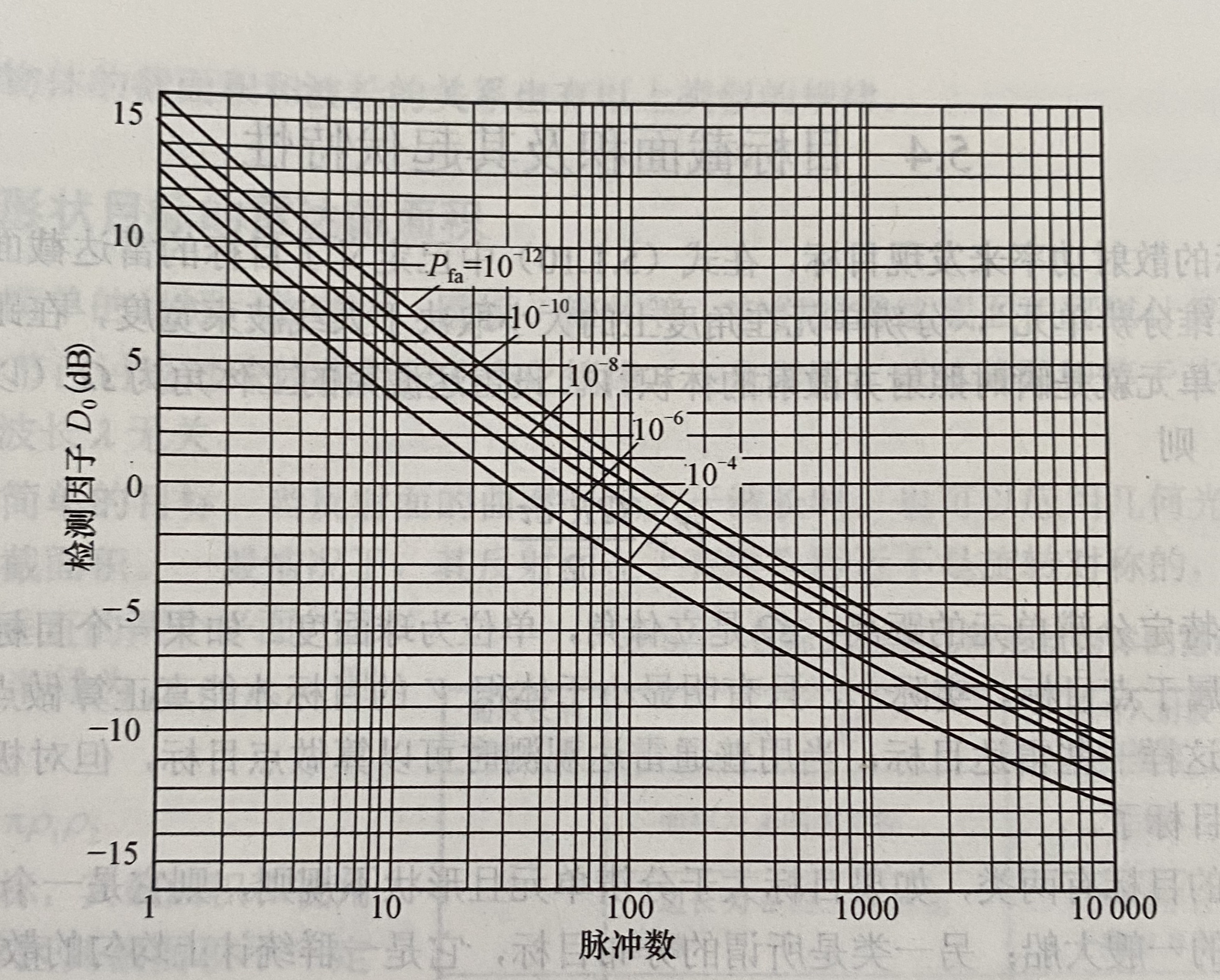
上面图中曲线的横轴表示非相参积累的脉冲数,纵轴是积累后的检测因子(D0),曲线表示检测因子D0随脉冲积累数M的变化规律,曲线族的参变量是不同的虚警概率Pfa。
- 线性检波非起伏目标检测因子(所需信噪比)与非相参脉冲积累数的关系,Pd=0.5
- 积累脉冲数的确定
当雷达天线进行机械扫描的时候,可积累的脉冲数(收到的回波数)取决于天线波束的扫描速度以及扫描平面上天线波束的宽度。
可以用公式计算方位扫描雷达半功率波束宽度内接收到的脉冲数N:

目标截面积及其起伏特性
脉冲雷达的特点是有一个“三维分辨单元”,分辨单元在角度上的大小取决于天线的波束宽度,在距离上的尺寸取决于脉冲宽度,此分辨单元就是瞬时照射的体积V。

如果一个目标全部包含在体积V中,便认为该目标属于点目标
- 点目标特性与波长的关系

球体截面积与波长的关系
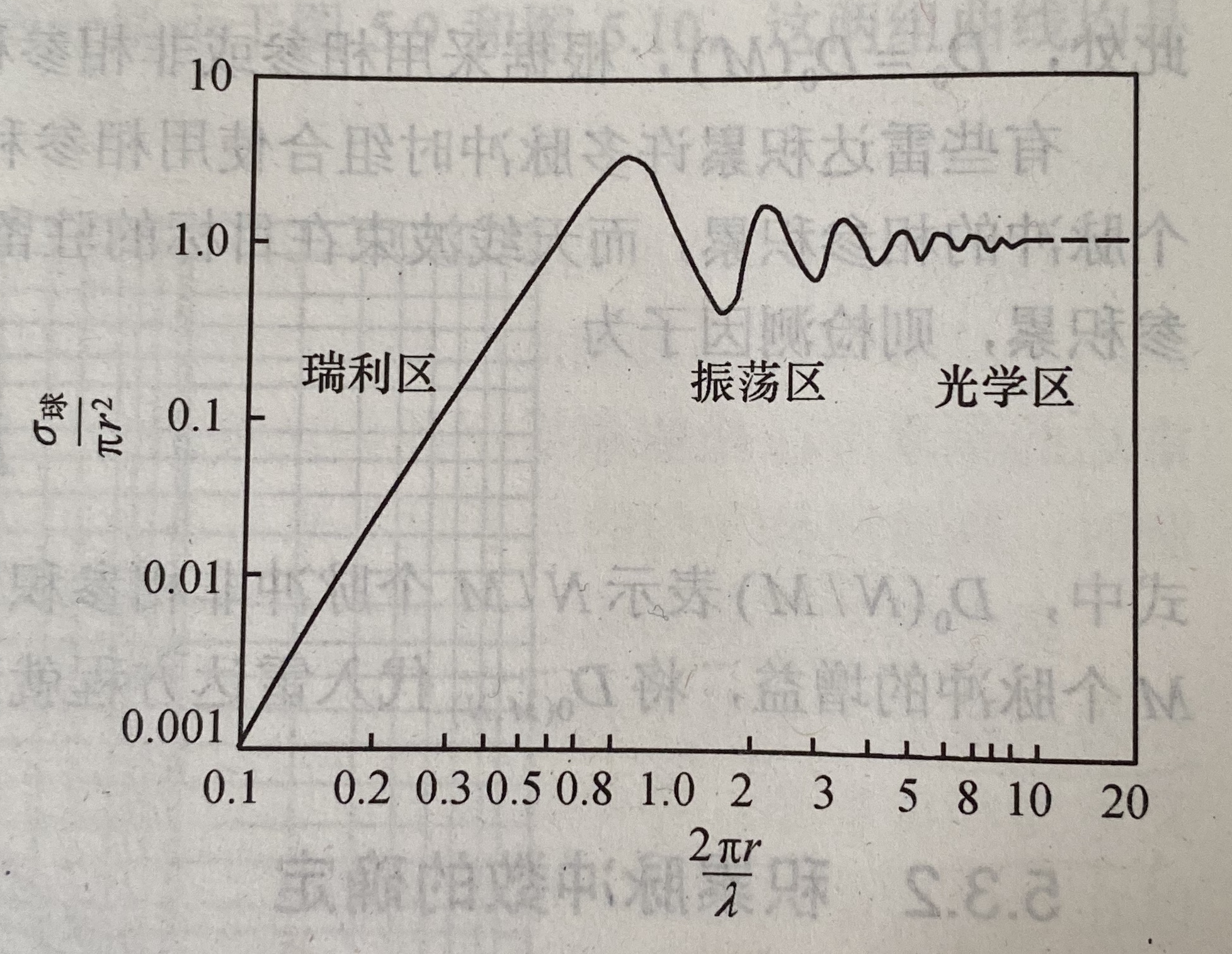
- 简单形状目标的雷达截面积
目标为简单几何形状物体的雷达参数

- 复杂目标的雷达截面积
目标雷达截面积举例:

- 目标发射特性与极化的关系
- 线极化
目标的散射特性通常与入射场的极化有关,照射到远区目标上的是线极化平面波,而任意方向的线极化波都可以分解为两个正交分量,即垂直极化分量和水平极化分量。- 一般情况

- 特殊形体目标的散射矩阵
- 各向同性的球体,散射矩阵为:
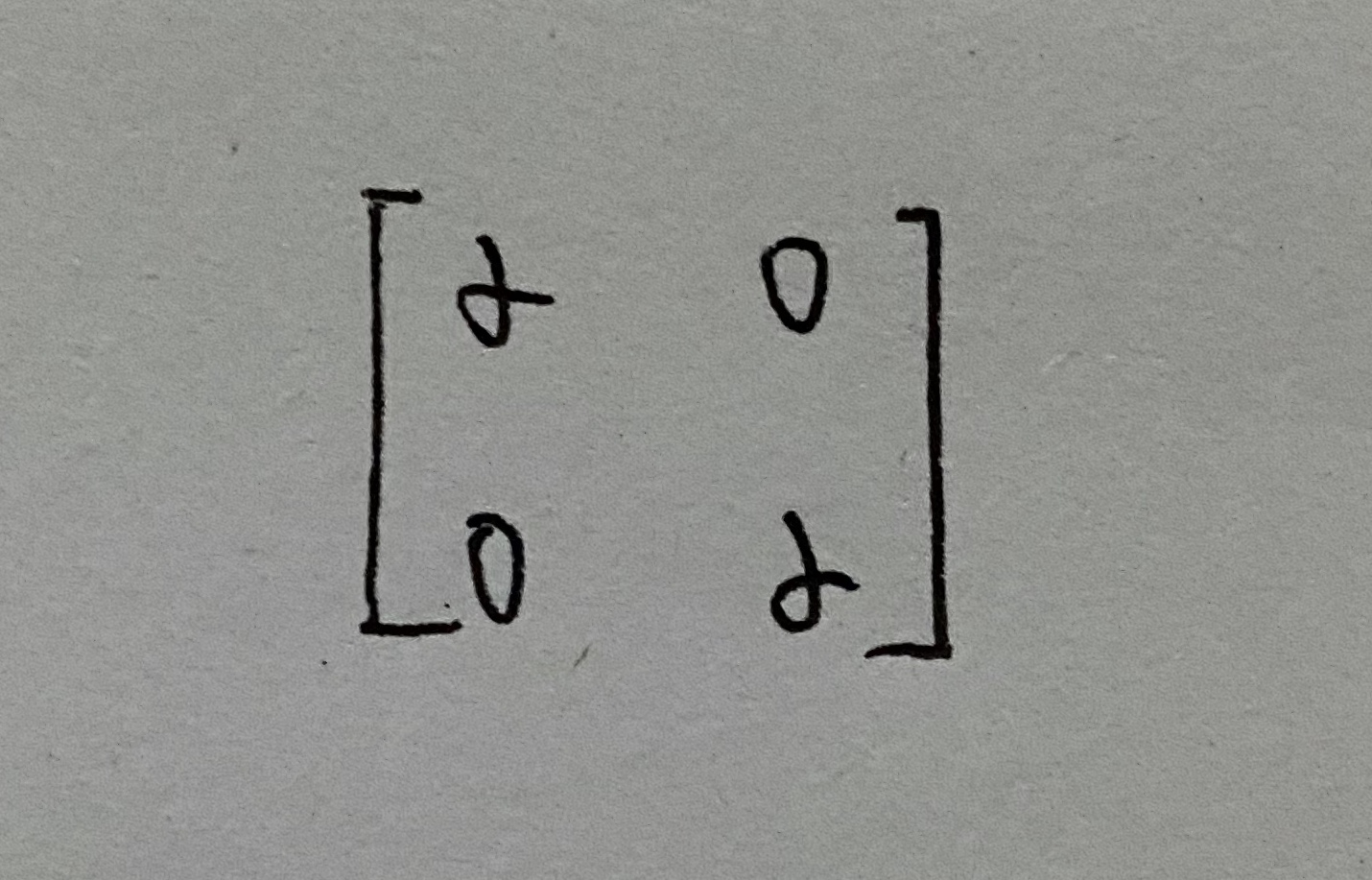
- 入射方向对称的物体,散射矩阵为:
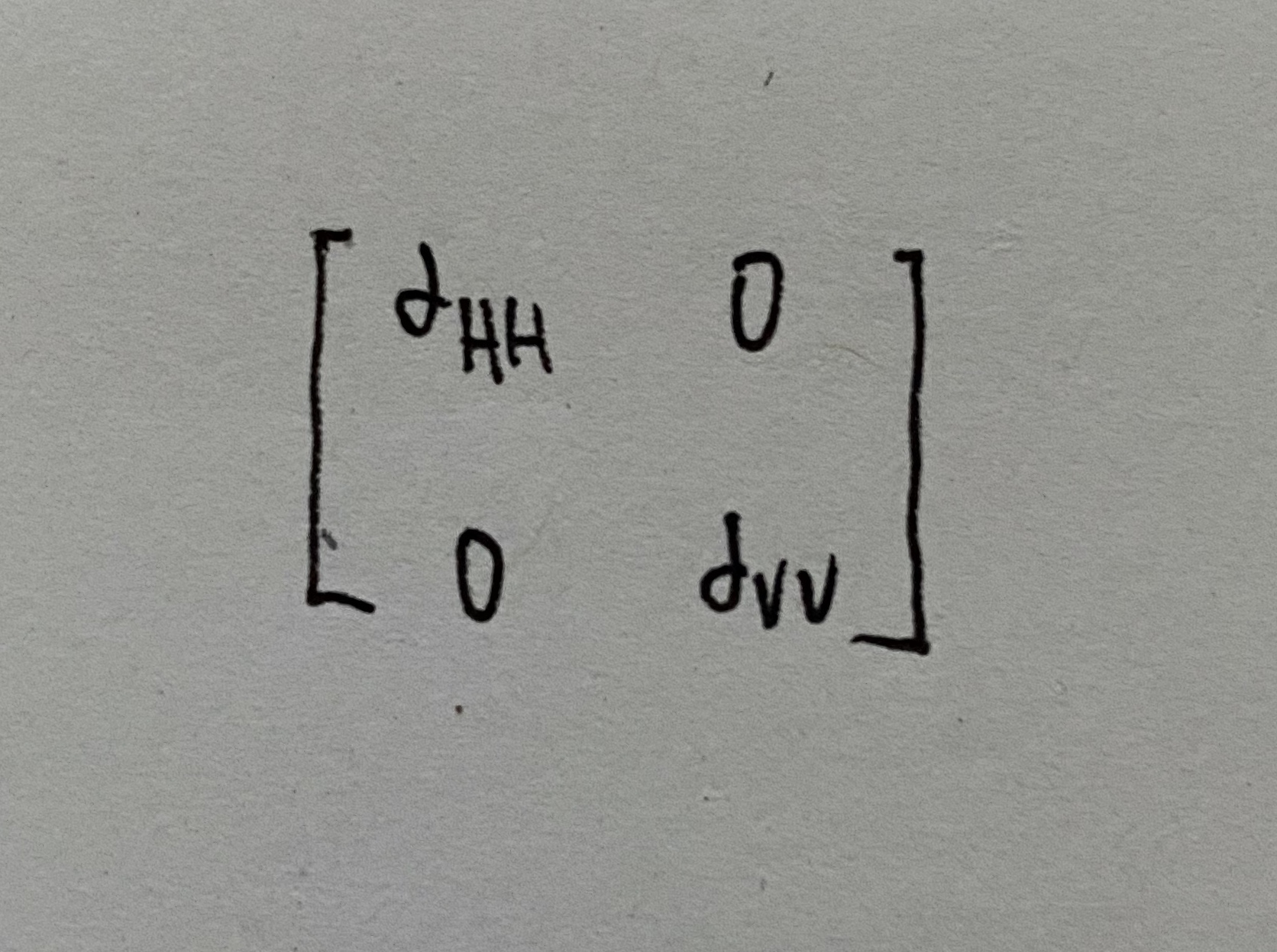
- 各向同性的球体,散射矩阵为:
- 一般情况
- 圆极化或椭圆极化
雷达天线辐射的是圆极化波或椭圆极化波- 一般情况

- 相对于视线轴对称的目标,散射矩阵为:
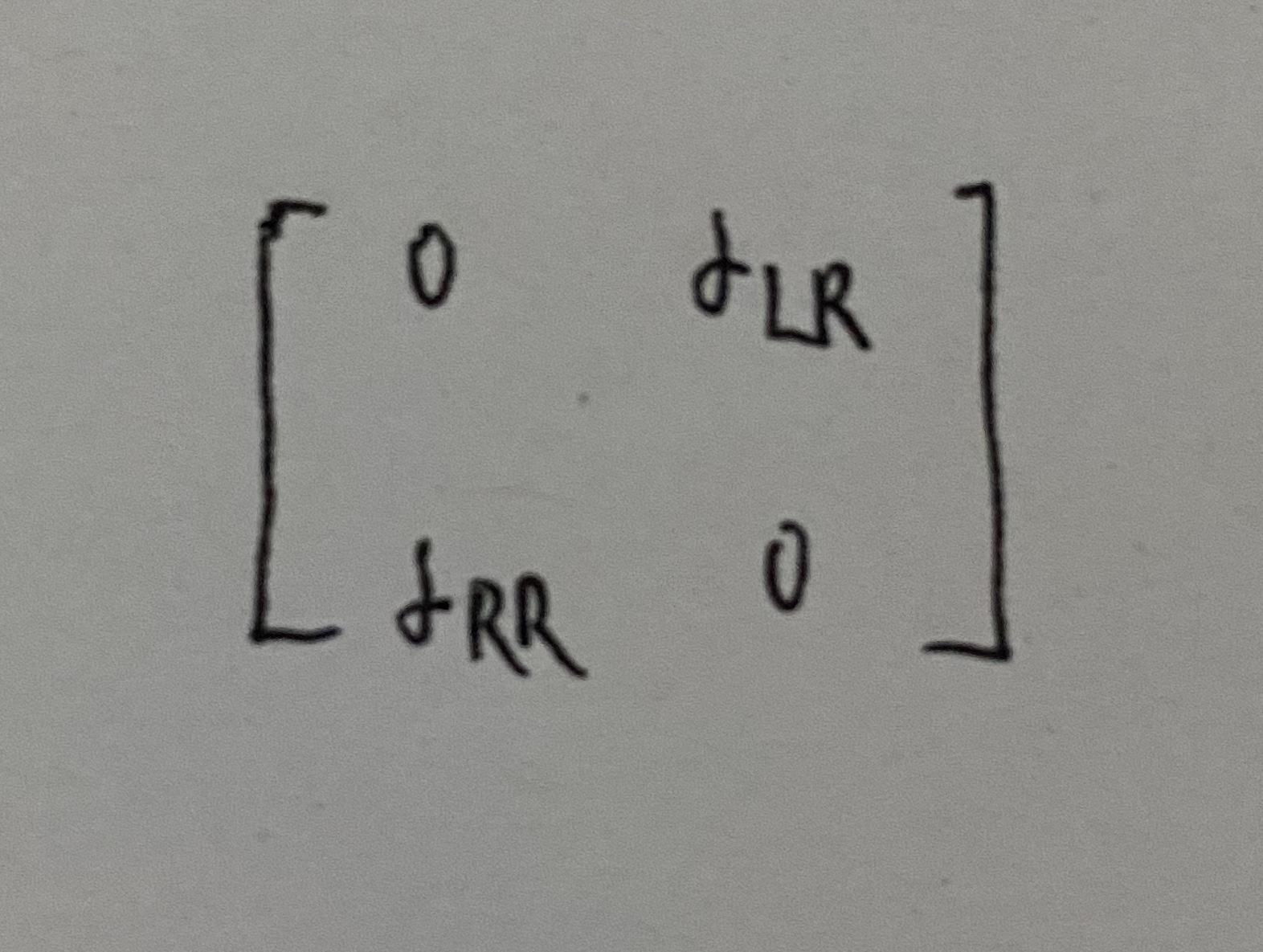
这是因为目标的对称性,反射场的极化取向与入射场一致并有相同的旋转方向,但由于传播方向相反,因而相对于传播方向其旋转方向亦相反,即对应于入射场的右(左)旋极化,反射场则变为左(右)旋极化。
如果采用相同极化的圆极化天线作为发射发射和接收天线,那么对于一个近似为球体的目标,接收功率很小或为零。
- 一般情况
- 线极化
- 目标起伏模型
处于运动状态的目标,视角一直在变化,截面积随之产生起伏,要正确地描述雷达截面积起伏,必须知道它的概率密度函数和相关函数,概率密度函数说明的是目标截面积的概率,而相关函数则描述雷达截面积在回波脉冲序列间的相关程度。- 施威林(Swerling)起伏模型
慢起伏目标:在天线一次扫描期间回波起伏是完全相关的,而扫描至扫描间完全不相关。
快起伏目标:他们的回波起伏在脉冲与脉冲之间是完全不相关的。
五种起伏模型:
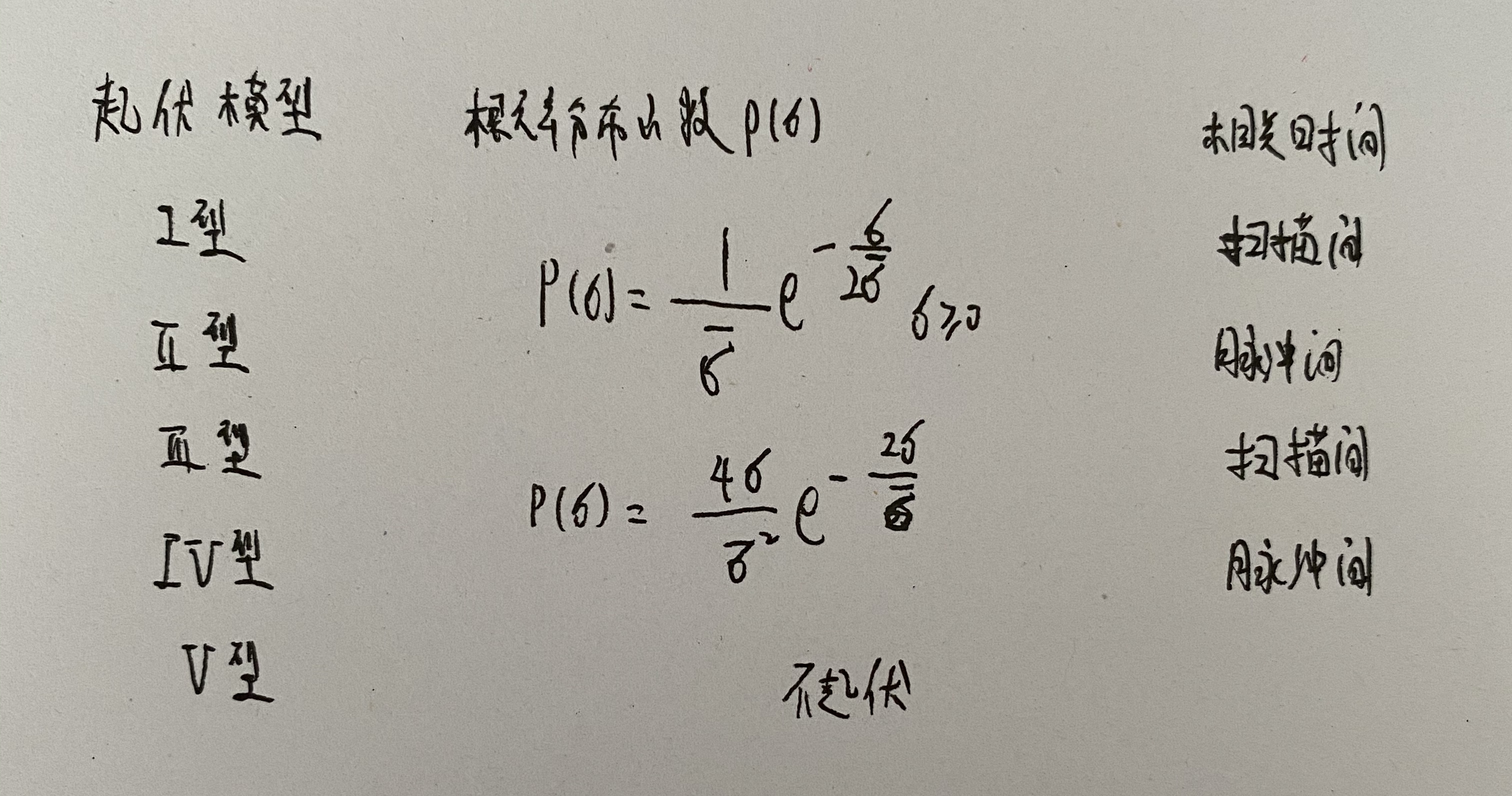
- 目标起伏对检测性能的影响
由于目标起伏,引起检测困难,导致D0增加
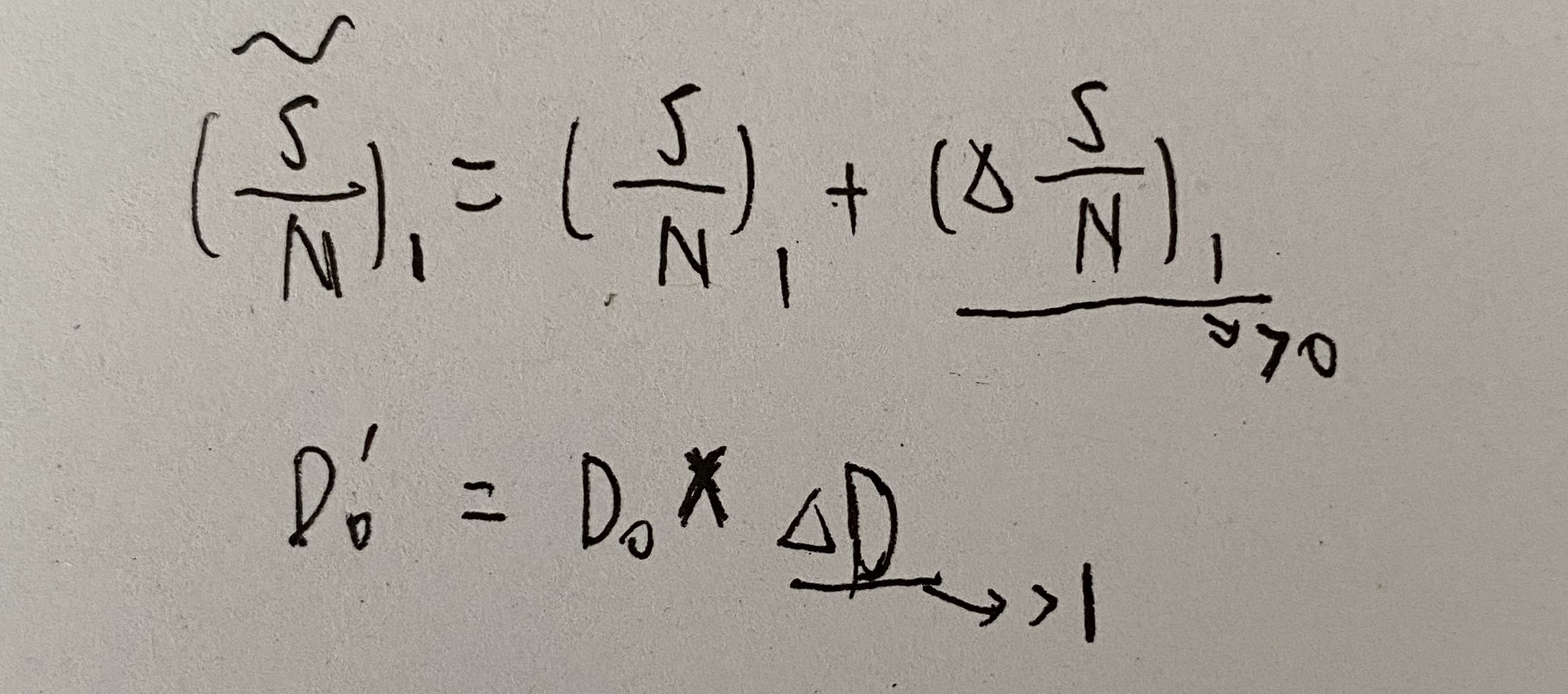
达到规定Pd时的起伏损失时,起伏目标比不起伏目标每一脉冲所需增加的信号噪声比,如下图:
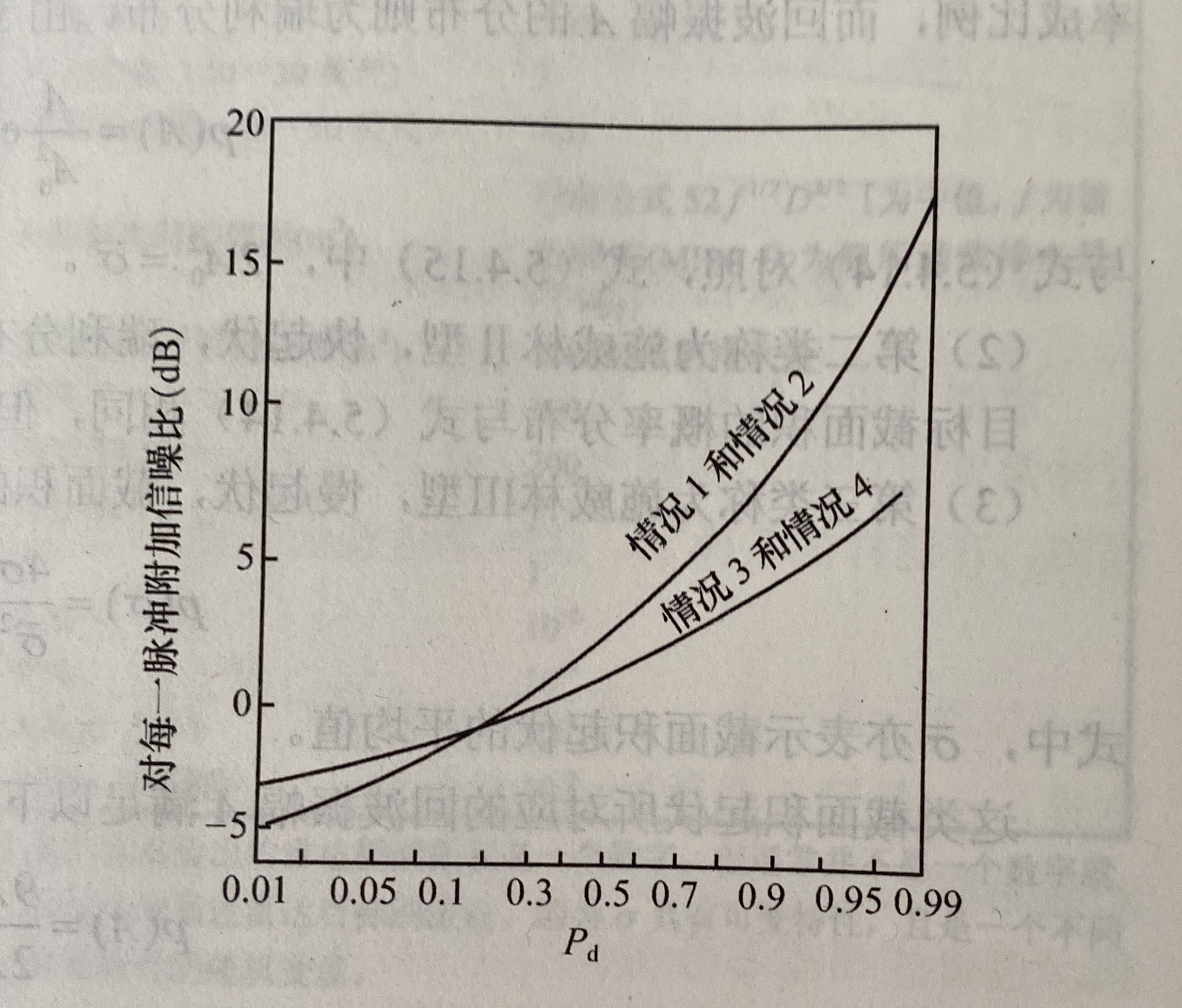
- 施威林(Swerling)起伏模型
系统损耗
-
系统损耗对雷达方程的影响
雷达方程:
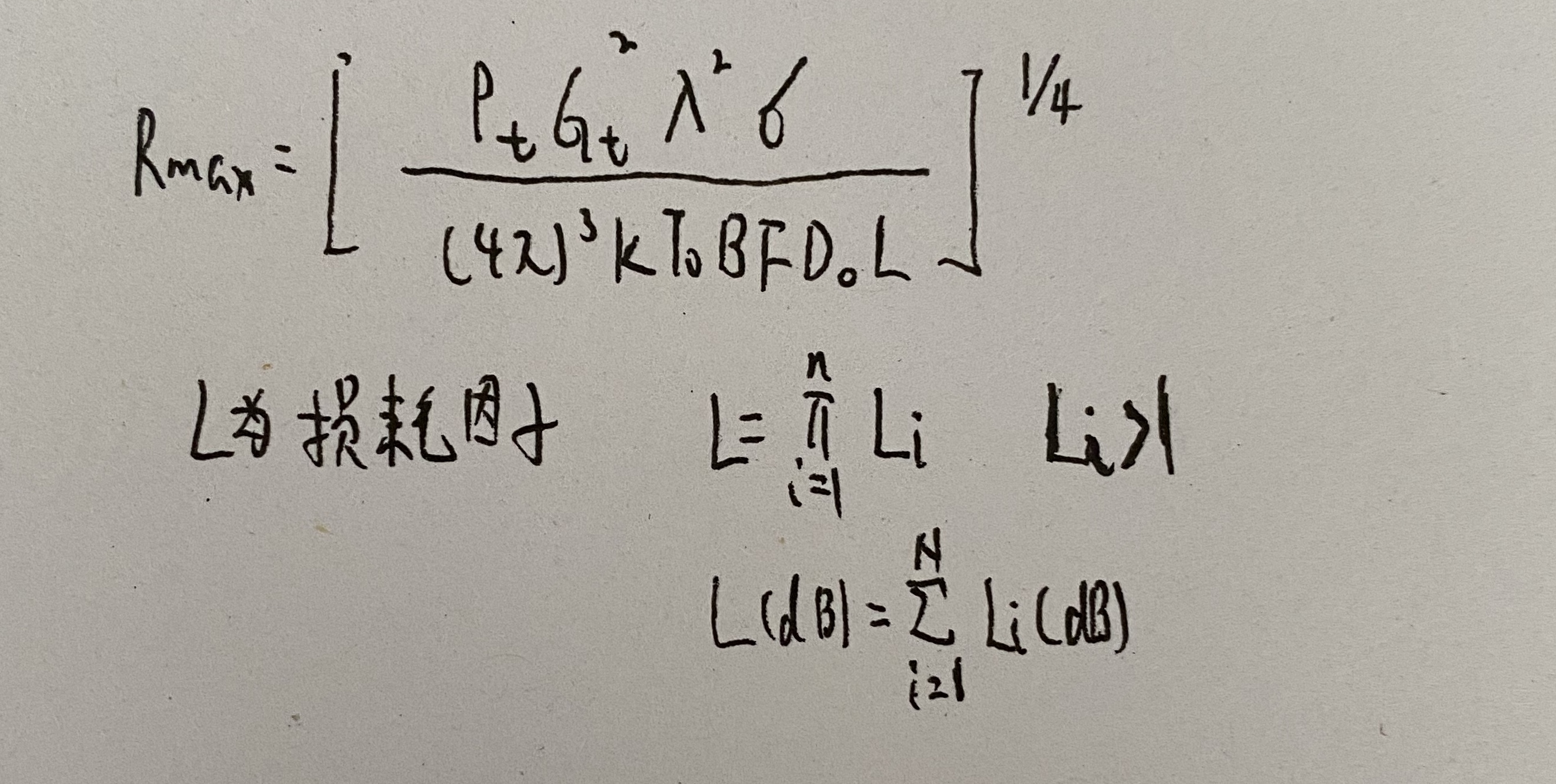
-
损耗分类
a. 射频传输损耗 b. 天线波束形状损失 c. 设备不完善损失
传播过程中各种因素的影响
- 大气衰减
大气中的氧气和水蒸气是产生雷达电波衰减的主要原因
下图给出了氧气和水蒸气的衰减曲线:
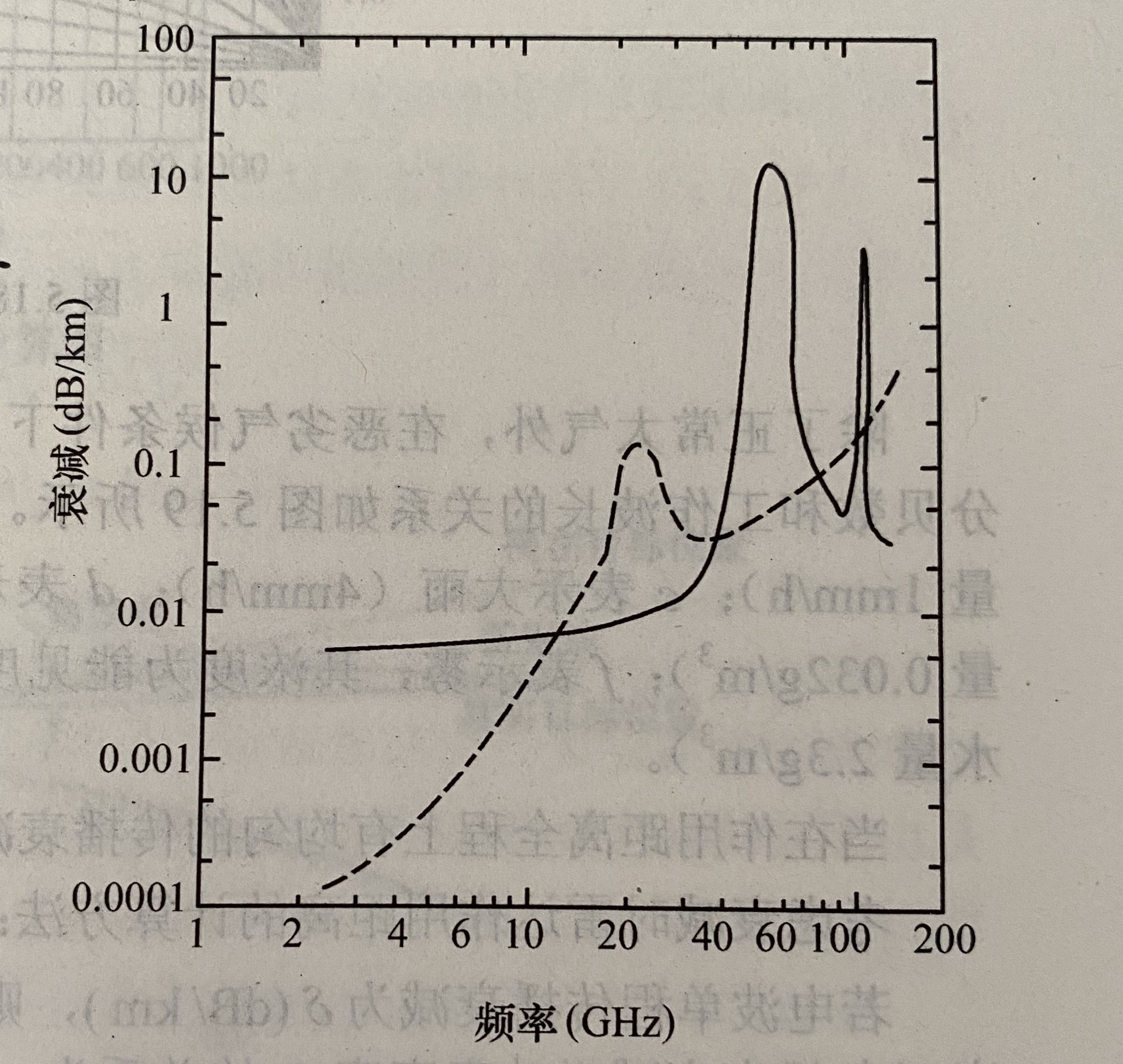
实线是氧气,虚线是水蒸气
水蒸气的衰减谐振峰发生在22.4GHz和184GHz
氧的衰减谐振峰则发生在60GHz和118GHz- 晴朗天气
随着高度的增加,大气衰减减小,因此,实际雷达工作时的传播衰减与雷达作用的距离以及目标高度有关。
下图给出了两种不同的仰角时的双程衰减分贝数- 仰角是0°时:
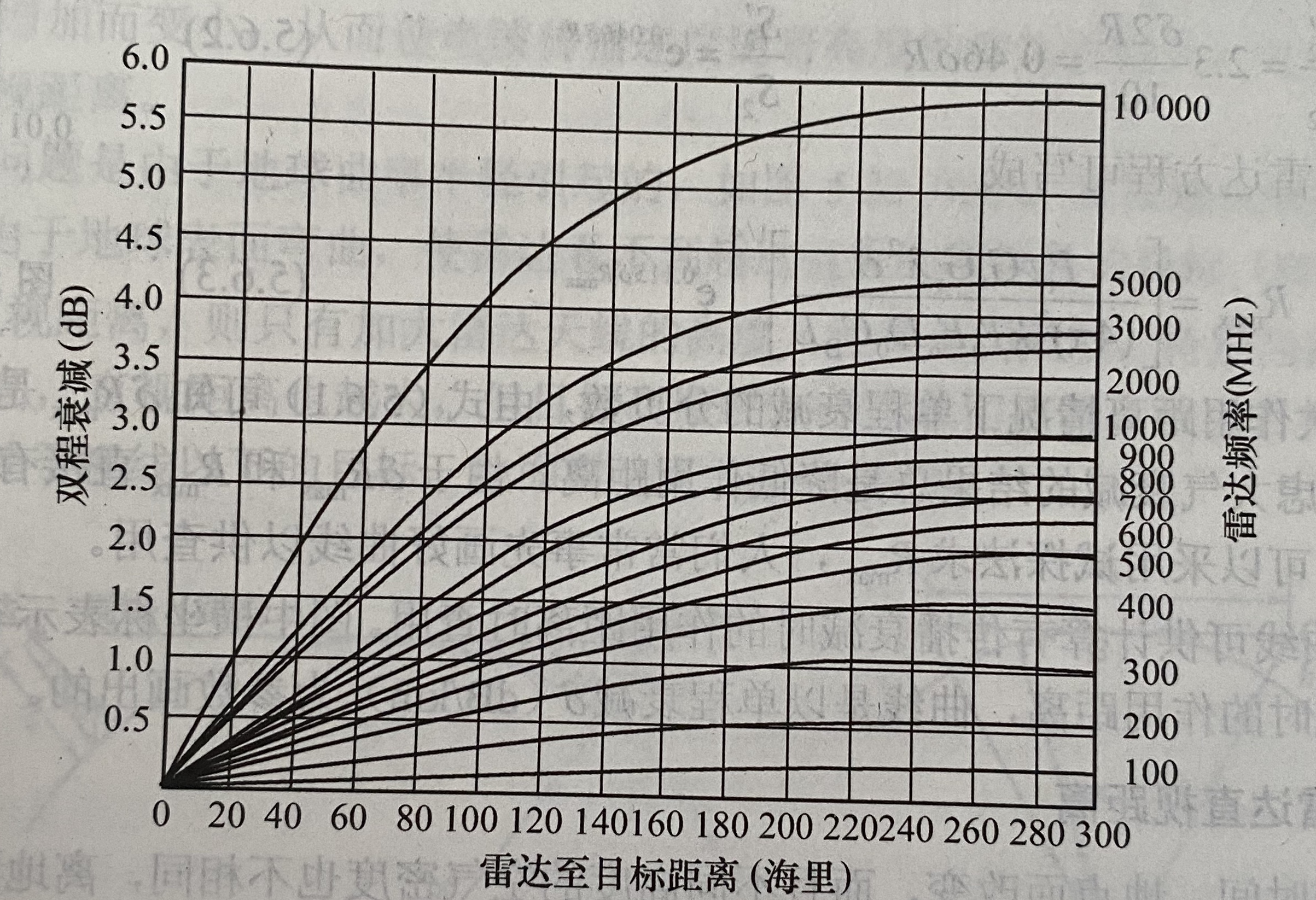
- 仰角是5°时:

- 仰角是0°时:
- 其他天气情况
各种气候条件下衰减分贝数和工作波长的关系如下图:
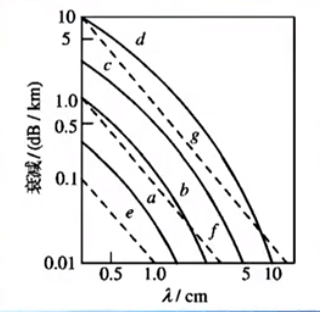
图中字母含义:
曲线a表示微雨(雨量0.25mm/h)
曲线b表示小雨(雨量1mm/h)
曲线c表示大雨(雨量4mm/h)
曲线d表示暴雨(雨量16mm/h)
曲线e表示雾,其浓度为能见度600m(含雨量0.032g/m3)
曲线f表示雾,其浓度为能见度120m(含雨量0.32g/m3)
曲线g表示雾,其浓度为能见度30m(含雨量3.2g/m3) - 下图所示的曲线可供计算有传播衰减时的作用距离查用
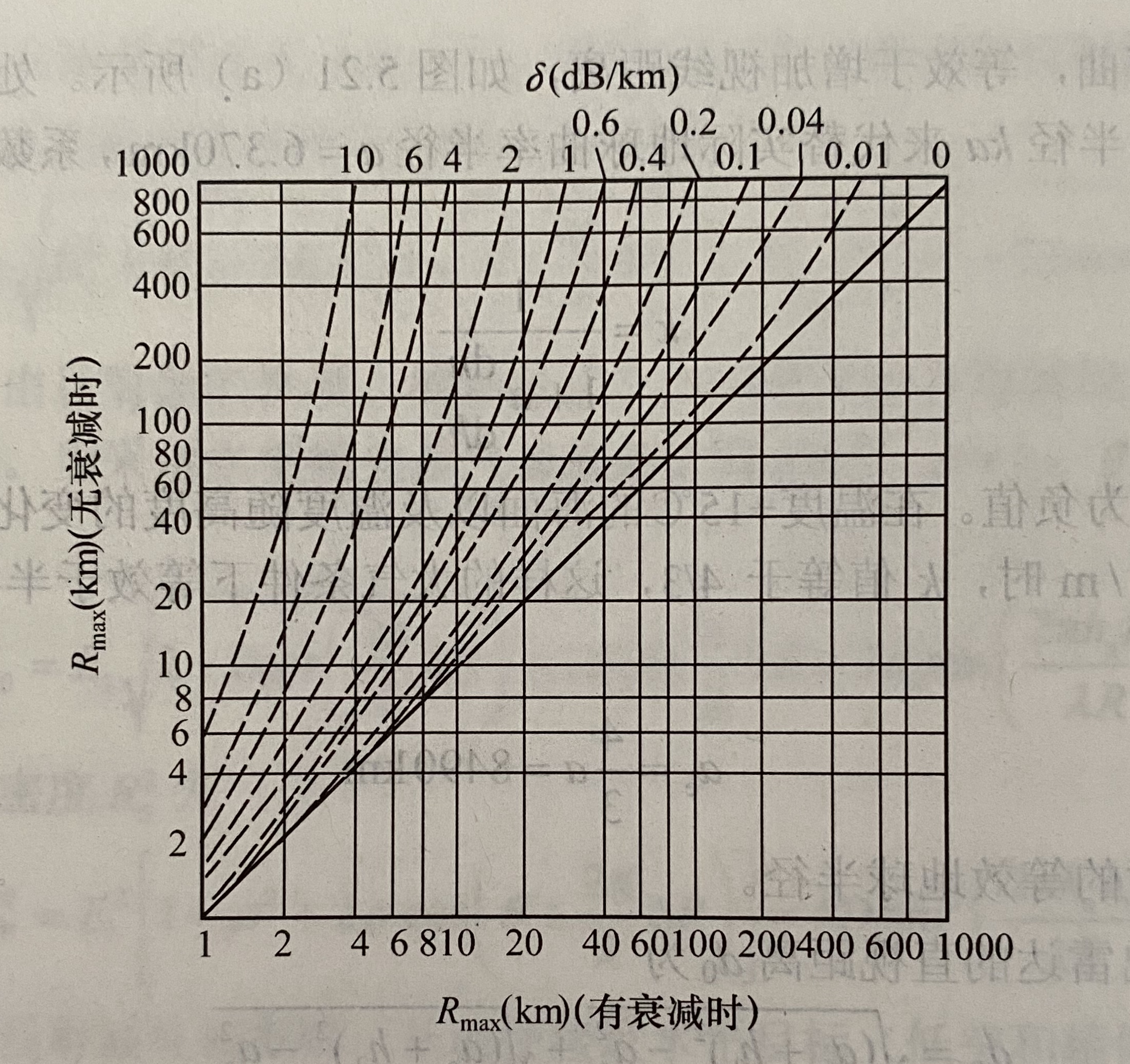
- 晴朗天气
- 直视距离
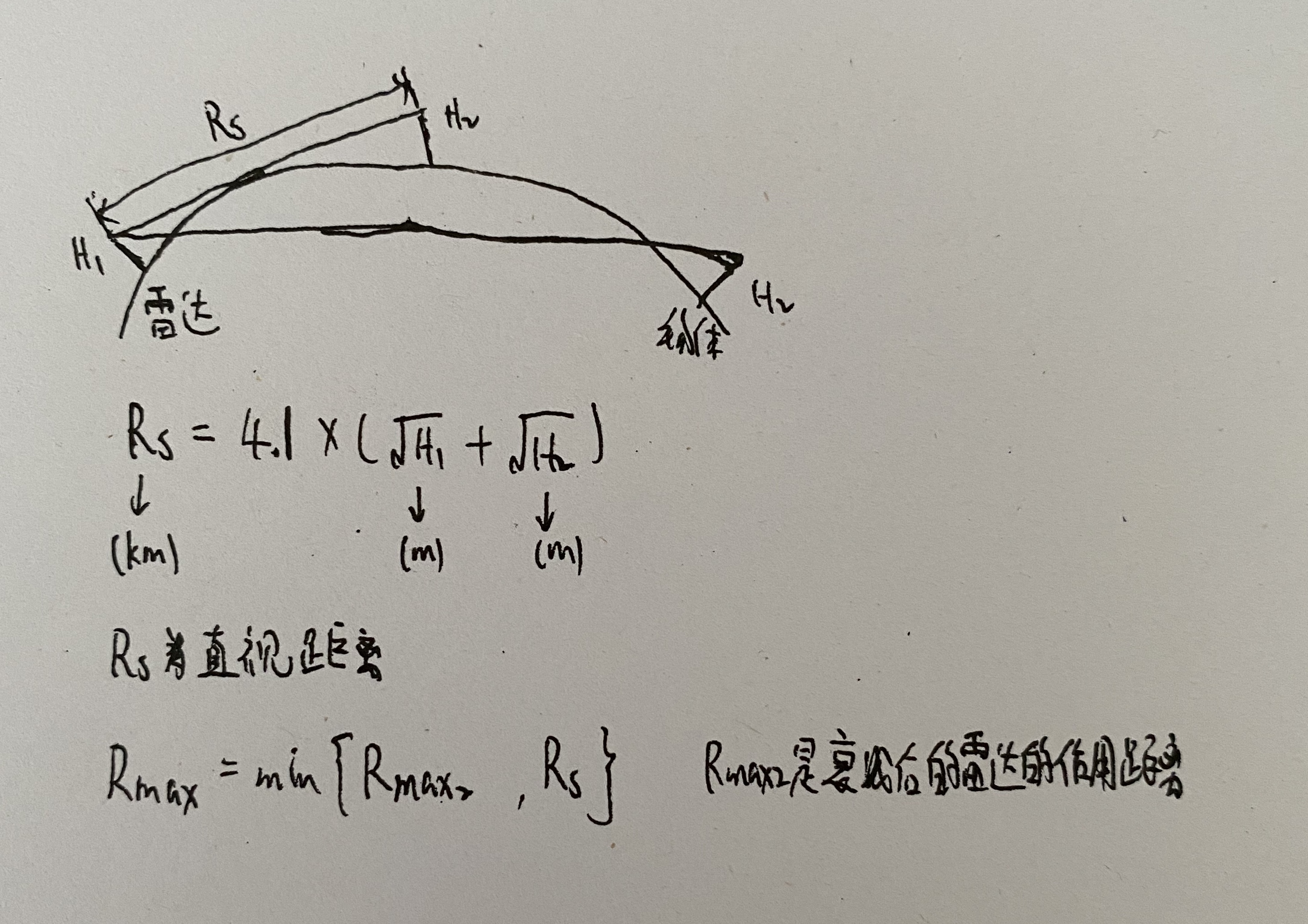
雷达方程的几种形式
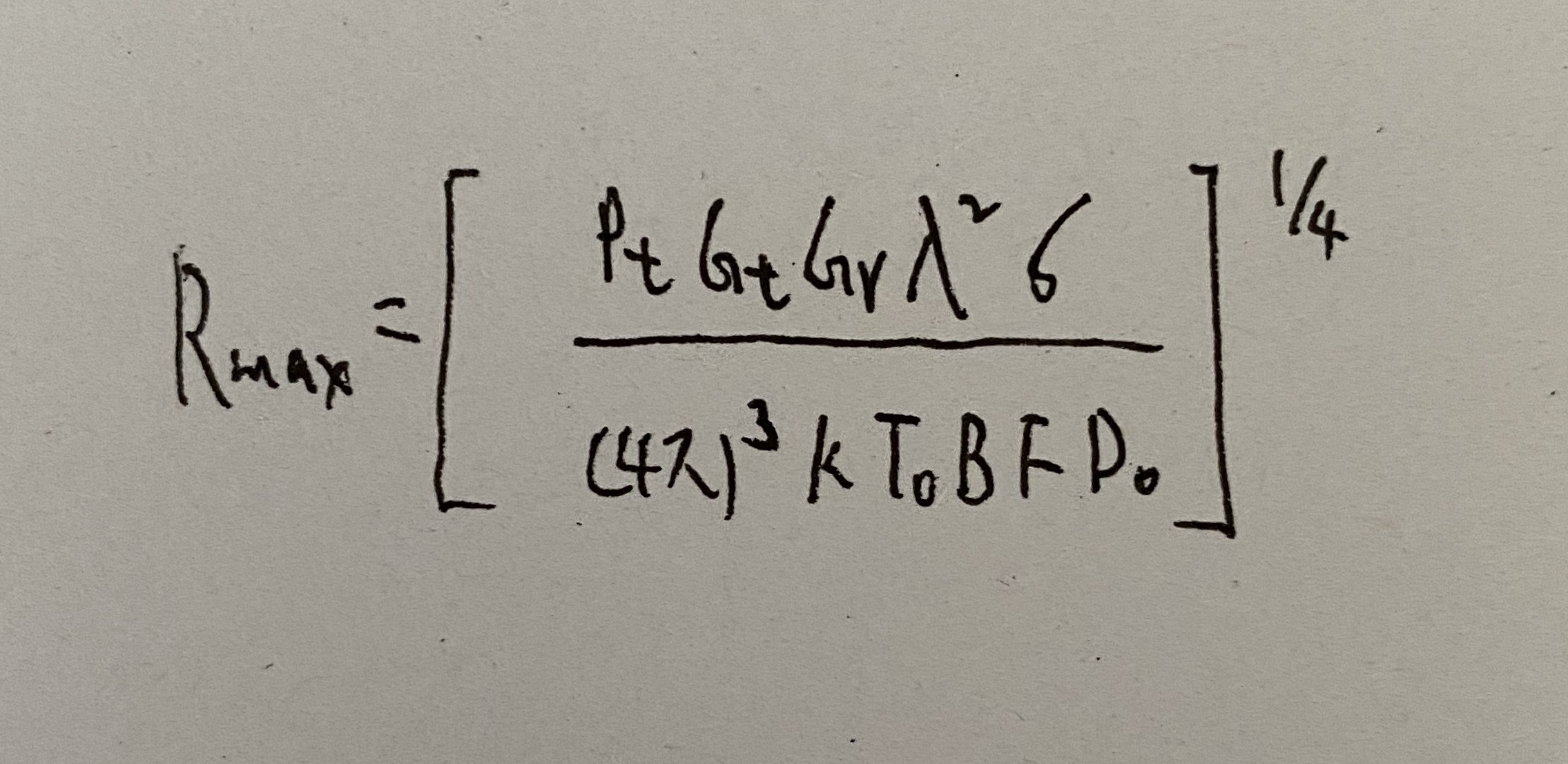
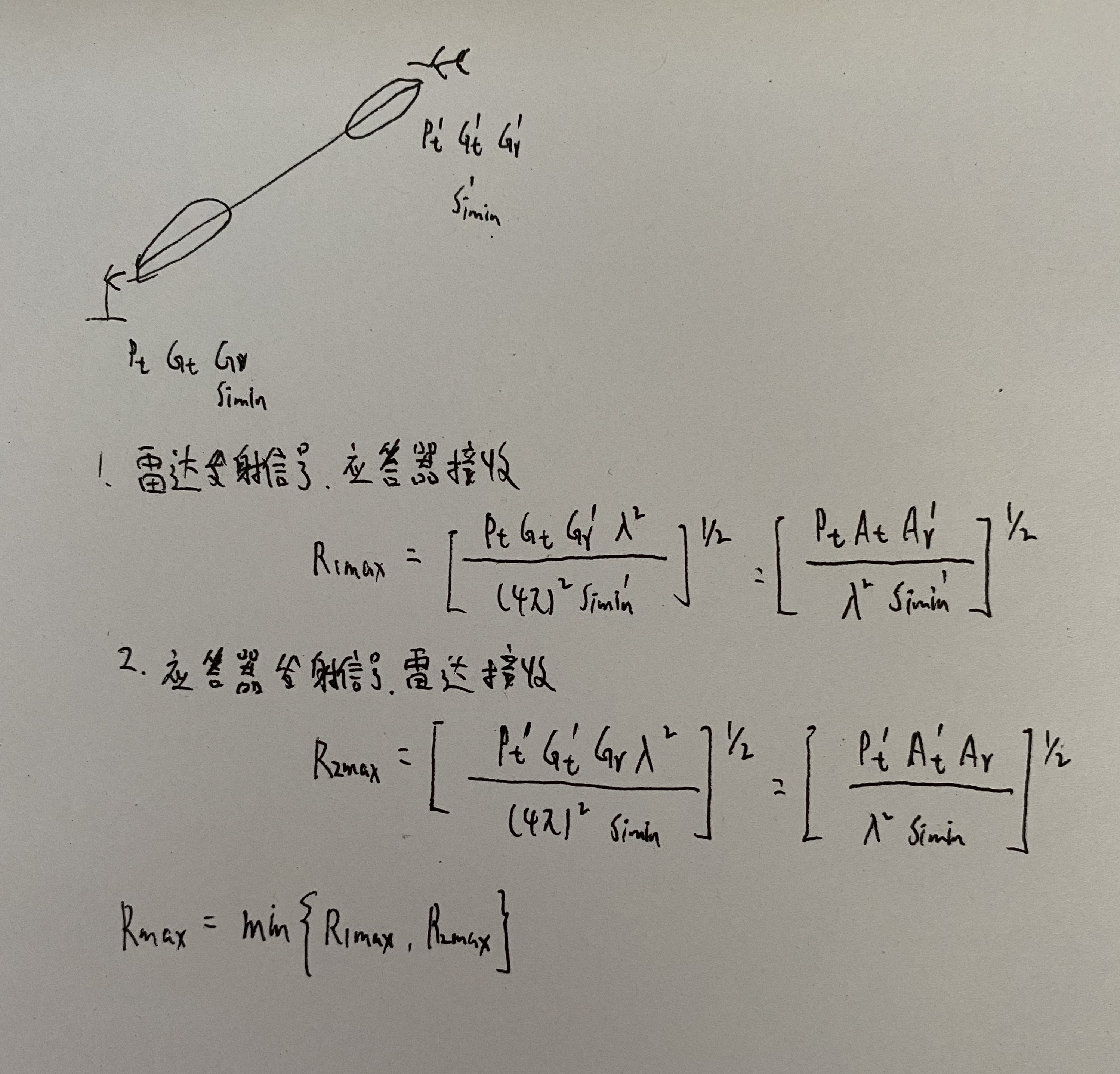
- 二次雷达方程
二次雷达是在目标上装有应答器(或目标上装有信标,雷达对信标进行跟踪),当应答器收到雷达信号以后,发射一个应答信号,雷达接收机根据所收到的应答信号对目标进行检测和识别
- 双基地雷达方程
双基地雷达是发射机和接收机分置在不同位置的雷达

- 用信号能量表示的雷达方程
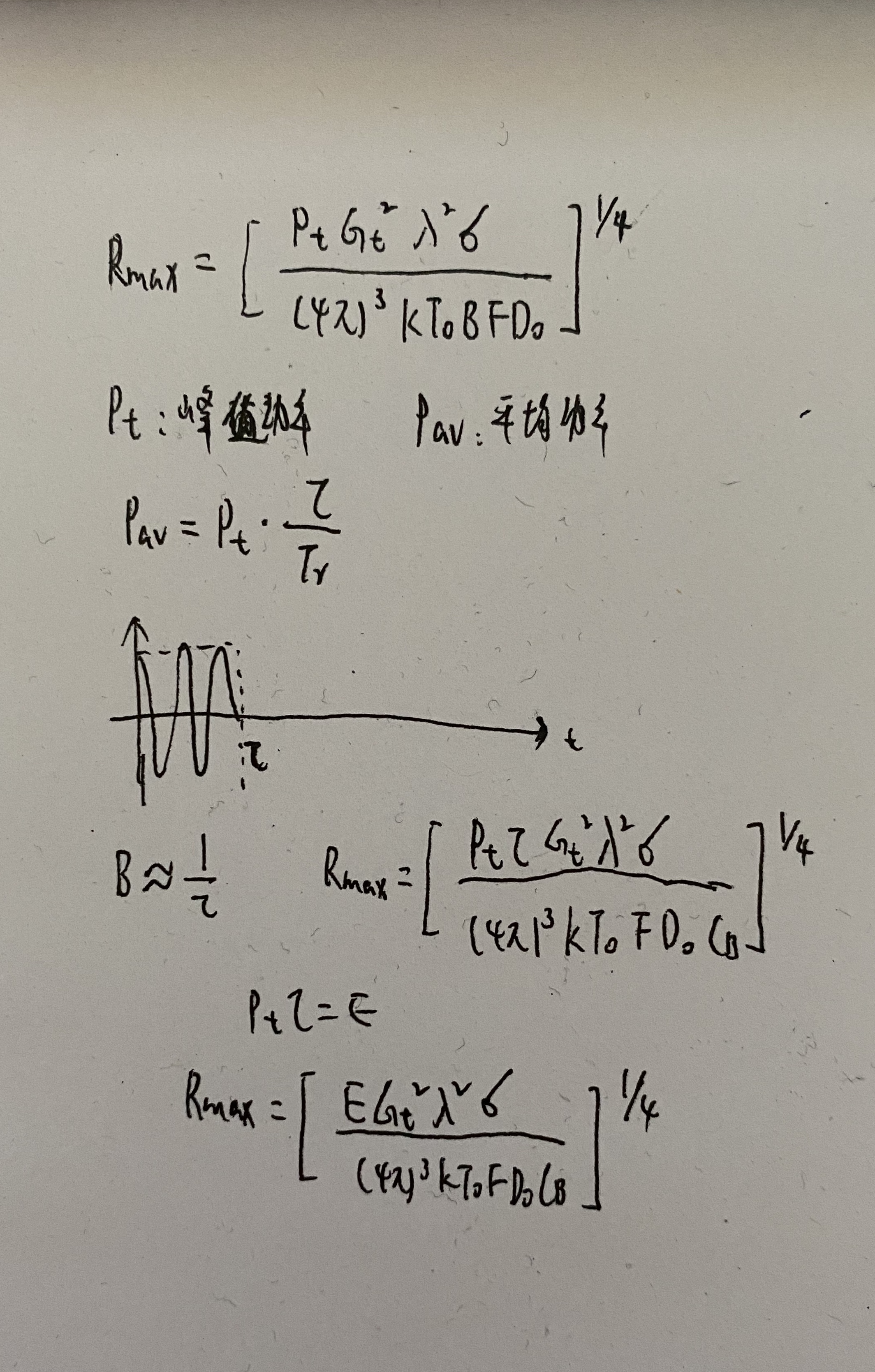
- 干扰环境下的雷达方程
有源干扰:受到敌方干扰机施放的干扰信号的干扰
无源干扰:受到散布在空间的金属带等发射形成的干扰- 有源干扰环境中的雷达方程

自卫干扰:将雷达的干扰机放在目标上
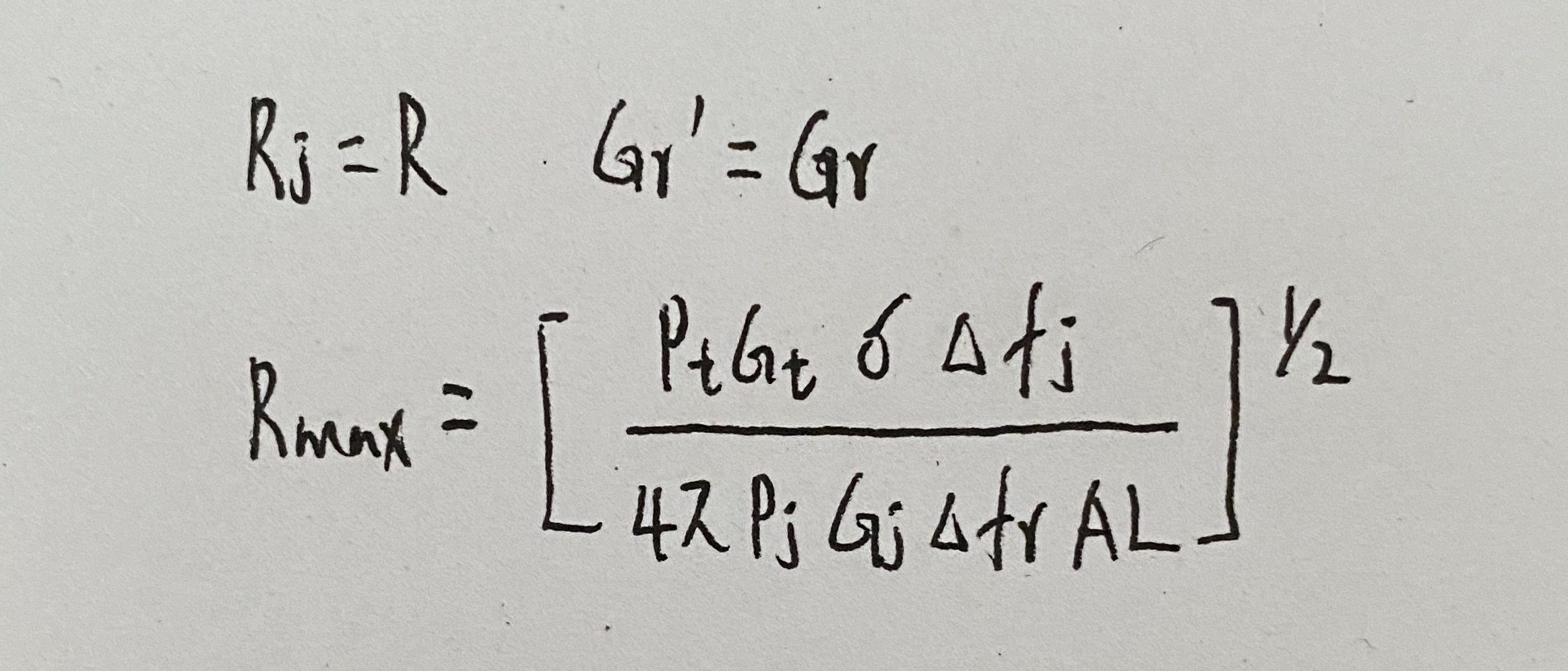
- 无源干扰环境中的雷达方程
无源干扰的主要形式是环境杂波和敌方施放的金属带条(箔条丝)

- 有源干扰环境中的雷达方程
当幸福来敲门
下面的是笔者的微信公众号,欢迎关注,会持续更新c++、python、tensorflow、机器学习、深度学习、计算机视觉、雷达原理等系列文章。

最后
以上就是优秀水杯最近收集整理的关于雷达原理-雷达作用距离雷达方程最小可检测信号脉冲积累对作用距离的改善目标截面积及其起伏特性系统损耗传播过程中各种因素的影响雷达方程的几种形式的全部内容,更多相关雷达原理-雷达作用距离雷达方程最小可检测信号脉冲积累对作用距离内容请搜索靠谱客的其他文章。








发表评论 取消回复