语音信号的预处理是语音信号进行后续处理的关键步骤,这里简单介绍下有关预处理的一些方法。语音信号的预处理一般包括:预加重、分帧、加窗等。
预加重
语音信号在经过声门激励和口鼻辐射影响时,其功率会有大幅度的衰减,而且语音信号的频谱中高频对应的能量的较小、低频对应的能量较大,所以未经处理的语音信号的高频部分更加难求,预加重的目的就是为了提高高频部分,使得语音信号的频谱变得平坦,进而在整个频带内可以用相同的信噪比求得频谱,便于频谱分析。预加重一般采用的是一阶高通滤波器
H
(
z
)
=
1
−
μ
z
−
1
Hleft( z right)=1-mu {{z}^{-1}}
H(z)=1−μz−1
其中,
μ
mu
μ的取值一般接近于1.
分帧
一般来说语音信号都是非平稳的,而分帧处理使得信号在帧内处于平稳状态便于后续处理。同时,为了使得帧与帧之间过渡平滑,前一帧与后一帧之间会有重叠的部分,称为帧移。帧移与帧长的比值一般取50%。
加窗
语音信号处理中常用的窗为矩形窗和汉明窗,其中矩形窗的表达式为
w
(
n
)
=
{
1
,
0
≤
n
≤
N
−
1
0
,
e
l
s
e
wleft( n right)=left{ begin{aligned} & 1, 0le nle N-1 \ & 0, else \ end{aligned} right.
w(n)={1, 0≤n≤N−10, else
汉明窗的表达式为
w
(
n
)
=
{
0.54
−
0.46
cos
[
2
π
n
/
(
N
−
1
)
]
0
≤
n
≤
N
−
1
0
,
e
l
s
e
wleft( n right)=left{ begin{aligned} & 0.54-0.46cos left[ 2pi n/left( N-1 right) right] 0le nle N-1 \ & 0, else \ end{aligned} right.
w(n)={0.54−0.46cos[2πn/(N−1)] 0≤n≤N−10, else
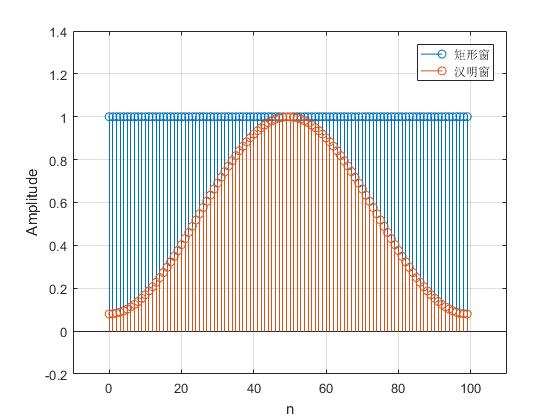
基于上述表达式可以得到它们的形状为
| 类型 | 主瓣宽度 | 旁瓣峰值 | 最小阻带衰减 |
|---|---|---|---|
| 矩形窗 | 4 π / N 4pi /N 4π/N | -13dB | -21dB |
| 汉明窗 | 8 π / N 8pi /N 8π/N | -41dB | -53dB |
一般来说,窗的形状和大小对后续的分析会有较大的影响。
窗的形状的影响
窗的形状在时域上减小窗口的坡度,使得窗口两端能够平滑过渡到零,进一步减小语音帧的截断效应;在频域上要具有较宽的带宽以及较小的边带。对于矩形窗来说,其在频域上的表达式为
H
(
e
j
ω
T
)
=
sin
(
N
ω
T
/
2
)
sin
(
ω
T
/
2
)
e
−
j
ω
T
(
N
−
1
)
/
2
Hleft( {{e}^{jomega T}} right)=frac{sin left( Nomega T/2 right)}{sin left( omega T/2 right)}{{e}^{-jomega Tleft( N-1 right)/2}}
H(ejωT)=sin(ωT/2)sin(NωT/2)e−jωT(N−1)/2
第一零点频率为
f
01
=
f
s
/
N
=
1
/
N
T
s
{{f}_{01}}={{f}_{s}}/N=1/N{{T}_{s}}
f01=fs/N=1/NTs
其中,
f
s
{{f}_{s}}
fs对应的为采样频率,
T
s
{{T}_{s}}
Ts对应的为采样周期。而汉明窗的第一零点频率比矩形窗要大很多,但是其在阻带内的衰减相应也要大上很多。
矩形窗以及汉明窗的傅氏变换如下
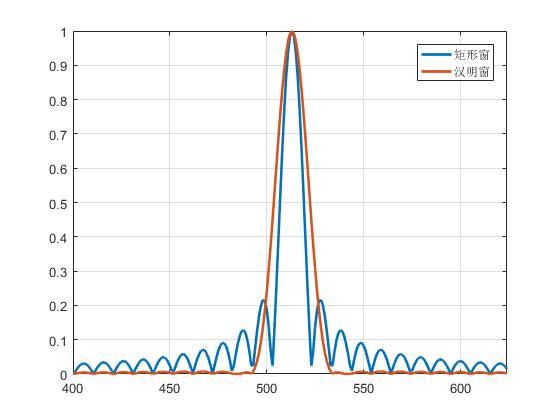
未取对数时,也可以看出两种窗的特性,比如矩形窗的主瓣较窄,旁瓣较高;而汉明窗的主瓣较宽,旁瓣较低,这也与上面的分析一致。为了明显地看出两者的区别,将其取对数后可以得到如下结果
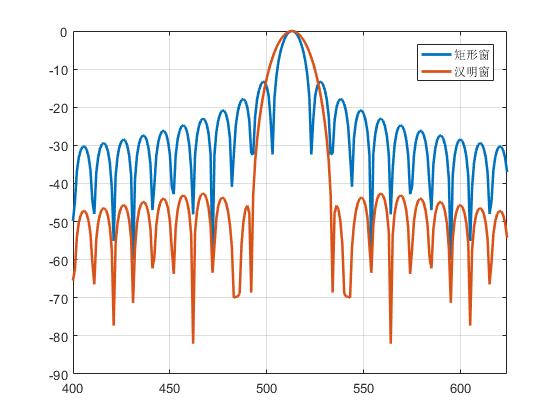
从图中可以看出,汉明窗的主瓣宽度要比矩形窗的主瓣宽度要宽很多,但是汉明窗的旁瓣要比矩形窗低很多。矩形窗的平滑性能较高,但是损失了高频成分,使得波形的细节方面丢失;汉明窗则与之相反。
窗的大小的影响
频率分辨率
Δ
f
=
f
s
N
=
1
N
T
s
Delta f=frac{{{f}_{s}}}{N}=frac{1}{N{{T}_{s}}}
Δf=Nfs=NTs1
当采样周期确定时,可以看出,频率分辨率
Δ
f
Delta f
Δf随着窗口大小
N
N
N的增加而逐渐减小,也就是说窗口越大,其频率分辨率越高,但是相应地时间分辨率就会降低;同样地,窗口大小减小时,频率分辨率下降,而时间分辨率提高,即时间分辨率和频率分辨率存在着矛盾的关系。另外,对于高斯窗函数来说,其时间分辨率和频率分辨率能取得较好的平衡。
进一步地,如果窗口大小
N
N
N很大,那么其等效为一个很窄的低通滤波器,当语音信号通过时,高频信息就会被滤除,短时能量随时间变化较小;而
N
N
N过小时,滤波器的带宽就会增加,短时的能量就会急剧变化,得不到平滑的能量的函数,因此在实际的问题的处理过程中,应当选取合适的窗函数。
代码如下
clear;
close all;
clc;
N=100;
n=(0:N-1);
w_rect = boxcar(N);
w_ham = hamming(N);
figure(1);
stem(n,w_rect);
hold on;
stem(n,w_ham);
xlabel('n');
ylabel('Amplitude');
axis([-10 110 -0.2 1.4]);
grid on;
legend('矩形窗','汉明窗');
N=1024;
w1_fft=fftshift(fft(w_rect,N));
w2_fft=fftshift(fft(w_ham,N));
figure(2);
plot(20*log10(abs(w1_fft)/max(abs(w1_fft))),'linewidth', 2);
hold on;
plot(20*log10(abs(w2_fft)/max(abs(w2_fft))),'linewidth', 2)
grid on;
legend('矩形窗','汉明窗');
xlim([400 624])
参考文献:
[1]赵力. 语音信号处理: 机械工业出版社 2016.
最后
以上就是幸福台灯最近收集整理的关于语音信号预处理原理介绍的全部内容,更多相关语音信号预处理原理介绍内容请搜索靠谱客的其他文章。








发表评论 取消回复