数字电路基础知识——格雷码和二进制码的转换的算法和Verilog实现

数字电路基础知识——格雷码和二进制码的转换的算法和Verilog实现

关于数字电路中的码制问题在这篇博客中已经做了详细分析，
数字电路基础知识——数字IC中的进制问题（原码，反码，补码以及各进制的转换）
这篇博客会再次详细分析一下数字IC设计中关于 格雷码（Gray Code） 的问题，在数字IC设计中格雷码的使用范围很广，格雷码由于其误码率底的有点基本上每个模块都会使用到格雷码。
近期在学习FIFO的时候碰到格雷码转换二进制码的问题。特此写这篇博客总结一下。

一、什么是格雷码

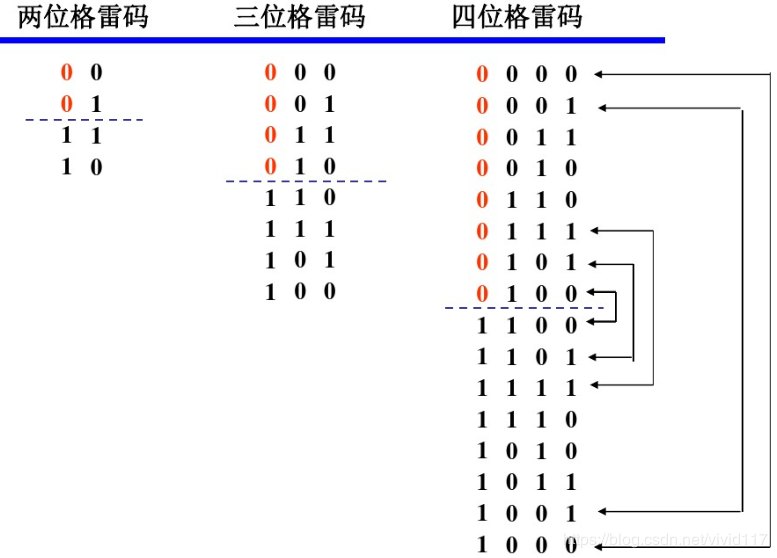
格雷码的每一位按照一定的顺序循环。如最右边的一位按照0110的顺序循环，右边第二位按照00111100的顺序循环。即自右向左0、1的循环数目翻倍。
格雷码的最主要特点：各个相邻码之间仅有一位状态不同，首尾也是仅有一位状态不同。

二、为什么要用格雷码

首先说下二进制码，在FIFO的设计中，在写请求中，写指针在写时钟作用下递增，在产生FIFO满信号时，需要将写指针和读指针进行比较，由于两个指针分别与其各自的时钟同步，但是彼此之间又是异步的关系，所以在使用二进制计数器实现指针的时候，就会出现比较的指针出现取样值错误的问题。
如从FFF到000可能会进行如下的转换

如果此时同步时钟边沿在FFF向000转换的时候，就可能会把上面的的三位二进制数的任何取样值同步到新的时钟域，导致数据错误。
所以采取的办法通常是使用格雷码计数

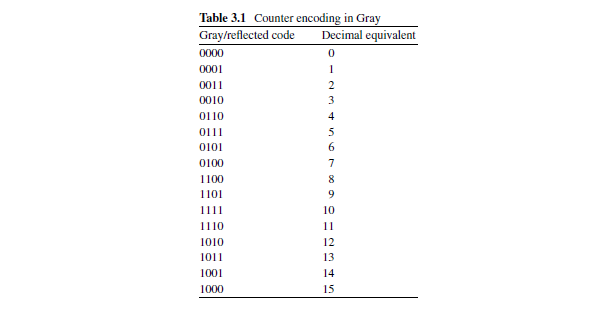
格雷码的优势在于一个数变为另一个数时，只有一位发生变化。

三、用格雷码实现FIFO指针

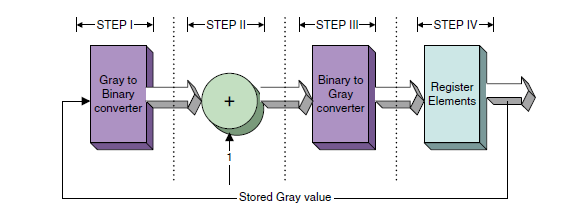
如果要产生完美的FIFO空或满条件，首先需要正确的读写指针，在时钟域传递指针的最好的办法就是使用格雷码来实现指针，这种编码能够消除绝大数错误。上面是格雷码的设计流程。

1. 将格雷码转换为二进制
2. 根据条件递增二进制值
3. 将二进制转换为格雷码
4. 将计数器的最终格雷码保存至寄存器中

四、由格雷码转换为二进制

1. 公式
   格雷码的转换公式：（i < n-1）
   
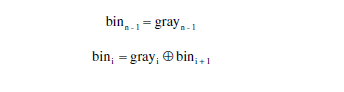
   计数器的位编号如下：
   MSB: Most Significant Bit的缩写，指最高有效位
   LSB: Least Significant Bit，指最低有效位
   
2. 例：将格雷码转换为相等的二进制数(@表示异或xor)
   i = 3,
   bin₃=gray₃ = gray[3] = 1
   i = 2,
   bin₂ = gray₂ @ bin₃ = gray₂ @ gray₃ = gray[2] @ gray[3] = 1
   i = 1,
   bin₁ = gray₁ @ bin₂ = gray₁ @ gray₂ @ gray₃ = gray[1] @gray[2] @gray[3] = 0
   i = 0,
   bin₀ = gray₀ @ bin₁ = gray₀ @ gray₁ @ gray₂ @ gray₃ = gray[0] @ gray[1] @ gray[2] @ gray[3] =0
   于是可以得到如下四个等式：
   
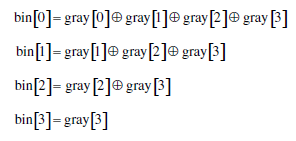
3. Verilog 语言描述格雷码转换为二进制码

module gray_to_bin (bin, gray);
parameter SIZE = 4;
input [SIZE – 1:0] bin;
output [SIZE – 1:0] gray;
reg [SIZE – 1:10] bin;
integer i;
always @ (gray)
for ( i = 0; i <= SIZE; i = i + 1)
bin[i] = ^(gray >> i);  		//右移一位并按位异或
endmodule

五、由二进制码转换为格雷码

1. 公式
   二进制向格雷码的转换公式：（i < n-1）
   
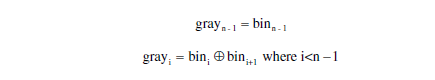
2. 例：将二进制转换为相等的格雷码(@表示异或xor)
   i = 3,
   gray₃ = bin₃ = bin[3] = 1
   i = 2,
   gray₂ = bin₂ @ bin₃ = bin[2] @ bin[3] = 0
   i = 1,
   gray₁ = bin₁ @ bin₂ = bin[1] @ bin[2] = 1
   i = 0,
   gray₀ = bin₀ @ bin₁ = bin[0] @ bin[1] = 0
   于是可以得到如下四个等式：
   
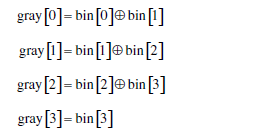
   由上式可以看出，通过逐位异或，或者将二进制码右移后与自己异或的操作方式，计算相应的格雷码，如下
   
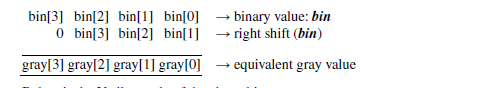
3. Verilog 语言描述二进制码转换为格雷码

module bin_to_gray (bin, gray);
parameter SIZE = 4;
input [SIZE-1:0] bin;
output [SIZE-1:0] gray;
assign gray = (bin >> 1) ^ bin;			//右移与自己异或
endmodule

六、格雷码计数逻辑的实现

由格雷码实现FIFO指针的流程图发现

module gray_ counter (clk, gray, inr, reset_n)
	parameter SIZE = 4;
	input clk, inr, reset_n;t
	output [SIZE -1 ] gray;
	reg [SIZE] – 1 ] gray_temp, gray, bin_temp, bin;
	integer i;
	
	always @ (gray or inr)
	begin:gray_bin_gray
		for (i = 0; i<SIZE ; 1 = i +1)
		bin[i] = ^(gray >> i); // gray to binary conversion
		bin_temp = bin + inr; // addition in binary
		gray_temp = bin_temp >> 1) ^ bin_temp; // binary to gray conversion
	end
endmodule

下面的逻辑快将转换后的格雷码值寄存起来

always @ (posedge clk or negedge reset_n)
begin:gray_registered
if (~reset_n)
	gray <= {SIZE {1’b0}};
else
	gray <= gray_temp;
end

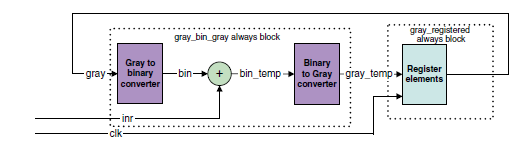
下图显示格雷码计数器的逻辑原理图：

最后

以上就是时尚哑铃为你收集整理的数字电路基础知识——格雷码和二进制码的转换的算法和Verilog实现的全部内容，希望文章能够帮你解决数字电路基础知识——格雷码和二进制码的转换的算法和Verilog实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。