P1_M5_L1 Proportional-Integral-Derivative(PID) Control（比例-积分-微分：PID控制）

1. Linear time-incariant (LTI) control （线性时不变控制）

1.1 汽车控制概述

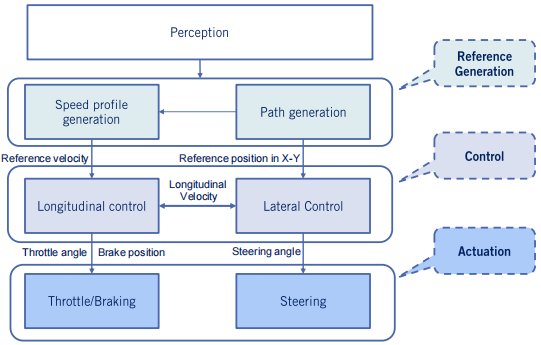
  当我们看到一辆无人驾驶汽车在拐弯时，我们会疑惑它是怎么做到的，下面就说一说实现拐弯的整个大致流程。
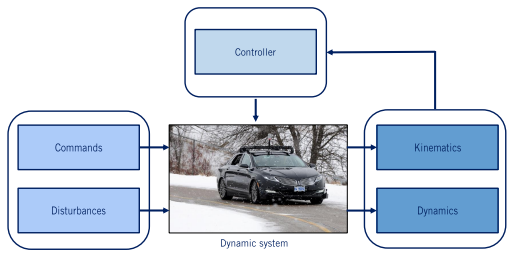
  前面我们讲过，无人车和外界的交互首先来源于环境感知，接着根据对环境的理解和需求做出相应的决策和规划，这时候已经得到了一条想要车辆接下来行驶的轨迹和速度。有了轨迹应该去真正的跑出来啊。。。这时候就需要一个控制器(controller) 去控制汽车了。
  但是，是不是直接把轨迹的信息丢给控制器呢？注意不是这样的。因为轨迹的信息是对整辆汽车而言的，也就是它表示整辆汽车的运动趋势；但控制器控制的是油门、脚刹、档位和方向盘，所以他需要的是后轮的速度和前轮方向的信息。所以还需要把轨迹的信息也就是无人车此时的指令(commands) 转化为控制器能够理解的控制信息。
  要实现这个转换，需要去分析汽车的构造和动力等等信息，记不记得前面所讲的运动学(kinematics)模型和动力学(dynamics)模型，那些模型最后总结出来的速度、加速度、角度等等之间的关系，其实就是为了设计控制器用的。所以，这两个模型实现了这一个转化过程。但是，别忘了汽车是开在路上的，而我们之前的汽车建模考虑了很少的环境干扰因素，所以这时候应该把环境的干扰(disturbances) 加入到轨迹信息中。
个人补充：其实把运动学模型和动力学模型嵌入到控制器里面，就可以实现直接从轨迹信息到实际控制。

1.2 线性时不变系统

线性时不变 = 线性+时不变
（1）线性：齐次性+叠加性
①齐次性：f(kx)=k*f(x)
②叠加性：f(a+b)=f(a)+f(b)
（2）时不变：即系统参数不随时间而改变，例如车辆的两个模型参数不随时间变化。

1.3 常见的反馈系统

这部分需要由控制理论的基础，下面这个系统是最简单的负反馈系统。

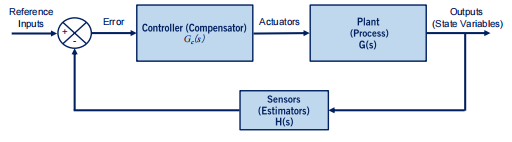
同时，拉普拉斯变换是控制理论最常用的东西。

 

2. PID Control（PID控制）

2.1 PID控制基本形式

（1）时域上：补偿量u(t)和偏差量e(t)的关系

（2）经过拉氏变换后：

（3）获得最关键的传递函数G(s)：表示补偿量与偏差之间的关系。

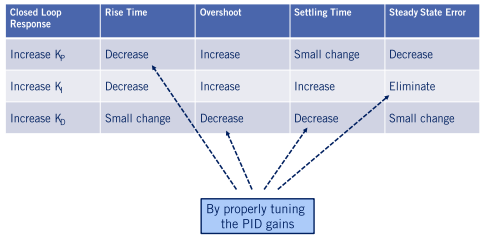
2.2 PID对应参数的调节效果

Rise Time（上升时间）
Overshoot（振荡）
Setting Time（稳定时间）
Steady State Error（稳态误差）

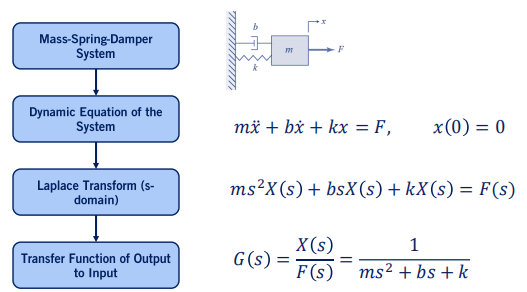
2.3 举例：二阶系统（重物弹簧阻尼系统）

重物弹簧阻尼系统→建立动力学方程→拉氏变换→得到位移和力的关系。

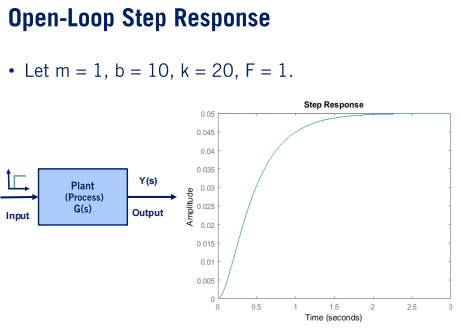
（1）开环系统（Open-Loop）：给定力，直接得到位移输出。

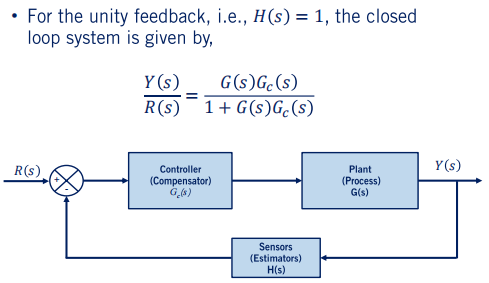
（2）闭环系统（Closed-Loop）：加上位移误差的负反馈

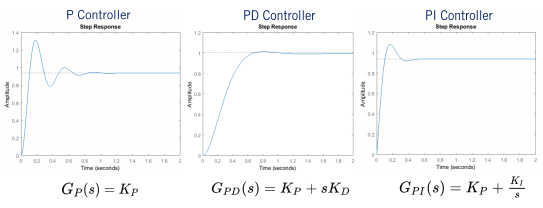
（3）除了使用PID控制，还可以只使用PID三个中的某几个：

最后

以上就是优雅故事为你收集整理的P1_M5_L1 Proportional-Integral-Derivative(PID) Control（比例-积分-微分：PID控制）的全部内容，希望文章能够帮你解决P1_M5_L1 Proportional-Integral-Derivative(PID) Control（比例-积分-微分：PID控制）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。