MATLAB系统辨识工具箱介绍（完结）

网上有比较详细的关于系统辨识工具箱函数的介绍，但是并没有根据相关实例进行讲解，因此让人看得云里雾里。这里我通过实例对MATLAB系统辨识工具箱函数进行详细讲解，帮助大家更容易理解系统辨识工具箱。

这个工具箱是一个处理离散采样数据，主要用最小二乘结构模型来进行辨识的一个软件包。它的结构设计比较合理、清晰、可扩展性好，因此为很多辨识理论研究者所采用，但其中递推算法涉及较少，需要使用者作二次开发。除此之外还有如神经网络辨识和控制辨识工具箱等的一些辨识软件。
可参考：
[1]张浩然,韩正之,李昌刚.基于MATLAB的神经网络辨识与控制工具箱[J].计算机仿真,2003(03):72-74+14.

Matlab的系统辨识工具箱提供了进行系统辨识的有力工具。系统辨识中的模型是考虑了噪声影响的随机模型。Matlab工具箱包括模型类和模型结构参数的确定两部分内容。利用Matlab编程环境，开发图形界面和多种辨识模型与算法等。模型类的确定主要是根据先验知识对过程的特性进行一定程度的假设，明确所要建立的模型是静态的还是动态的，是连续的还是离散的、是线性的还是非线性的、是参数模型还是非参数模型。支持的模型类主要有：非参数模型类中的脉冲响应模型；参数模型中的（ARX）模型、（ARMAX）模型、Box-Jenkins模型和状态空间模型等。在模型结构确定以后，就可以进行模型参数的辨识了，Matlab中对模型进行参数辨识方法包括最小二乘法、误差预报估计法、辅助变量法、几何网络法等。

一、辨识的基本理论

对于一个系统，在输入输出数据的基础上，从一组给定模型类中，确定一个与所测系统等价的模型，这种方法叫做辨识。

这个定义明确了辨识的三大要素：系统的输入输出数据（数据集）、模型类和等价准则（准则函数）。

系统的测得数据用$h(k)$表示，输出用$z(k)$表示，辨识模型的输出估计为$\hat{z}(k)$，实际输出与它的偏差为$\tilde{z}(k)$。辨识就是通过某种算法，利用模型输出与实际输出间的误差不断纠正模型参数，最终得到最优模型的过程。

在具体的辨识过程中，应该如何选择辨识函数呢？每个辨识算法都对应于特定的模型类型，所以应先选定模型类，再选择辨识算法及辨识函数。

辨识常见的几类模型如下：

1. ARX模型
   $A(z^{-1})y(k)=B(z^{-1})u(k-n_k)+e(k)$
2. ARMAX模型
   $A(z^{-1})y(k)=B(z^{-1})u(k-n_k)+C(z^{-1})e(k)$
3. Box-Jenkins模型
   $y(k)=\frac{B(z^{-1})}{F(z^{-1})}u(k-n_k)+\frac{C(z^{-1})}{D(z^{-1})}e(k)$
4. 通用线性模型
   $A(z^{-1})y(k)=\frac{B(z^{-1})}{F(z^{-1})}u(k-n_k)+\frac{C(z^{-1})}{D(z^{-1})}e(k)$

二、MATLAB系统辨识工具箱实例介绍

2.1 实例介绍

有一个加热的系统，其加热原理是在其入口处采用网状电阻丝对其内空气进行加热，原理如同吹风机，此系统的输入为供给电阻丝的能量，系统输出时加热系统出口处空气的温度。这是典型的线性SISO系统，此系统包含1000 个输入输出数据，现在要根据系统的输入输出数据找出描述系统特性的最佳模型。

该次对加热系统采用的是ARX模型，其表达式为：
$A(z^{-1})y(k)=B(z^{-1})u(k-n_k)+e(k)$

2.1 进入系统辨识工具箱界面

两种方法，第一种：
打开应用程序栏的系统辨识工具箱，

第二种，直接在命令行窗口输入“ident”：

进入界面后，弹出如下窗口：

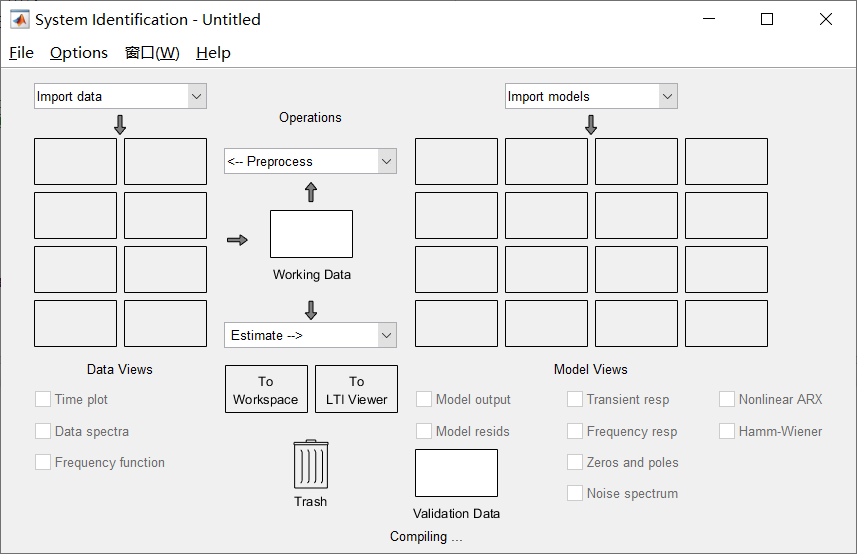
2.2 加载数据

由于此例子是MATLAB自带的，其名称为’dryer2’，因此直接load即可：

load dryer2

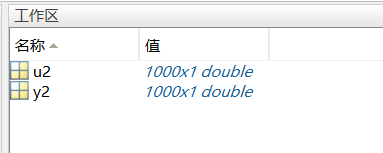
可以看到在工作区窗口中出现了两组数据u2和y2，这两组数据正是上面所说加热系统的输入和输出数据u2为输入，y2为输出。

2.3 导入数据

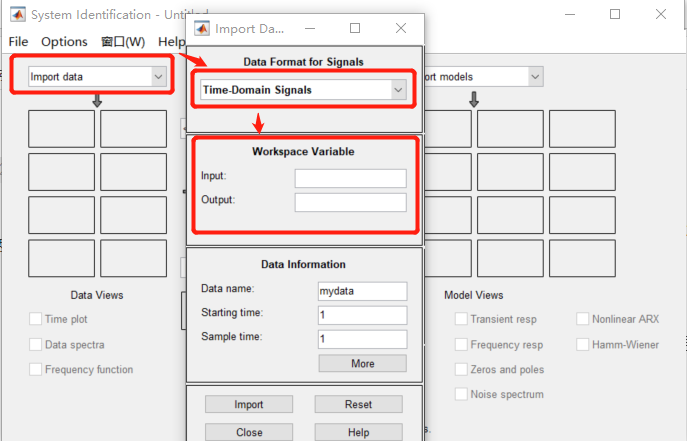
选择import data（输入数据）——>time domain signals（时域数据）——>
input：u2
output：y2
这里的两个输入栏是用来输入上面所说的系统输入和输出信号；
data name中输入的是辨识数据名称，默认为mydata，这里为了区分，修改为data；
starting time：辨识的起始时间，一般取0；
samping interval：输入的是采样间隔（单位为s），这里的间隔时间要由具体的实验情况而定，这里采用0.08s
所有输入好后界面如下：

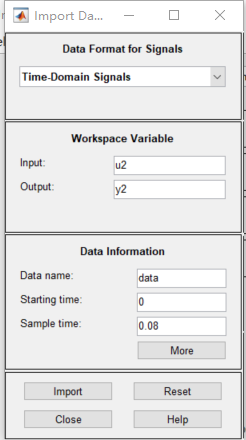
输入完成后点击import按钮，可以看到刚才设置的名为data辨识数据已经被导入GUI中。

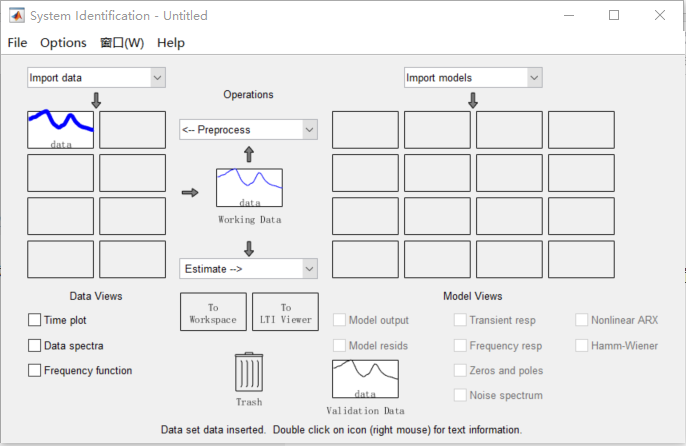
2.3 数据画图（数据预处理）

数据画图也就是将导入的数据生成图表，数据预处理包括对前面导入的data 数据进行去偏移，以及将数据分成估计模型数据和验证模型数据两部分。

勾选GUI 界面的time polt 图框会弹出原始数据的图表界面，如下图所示。

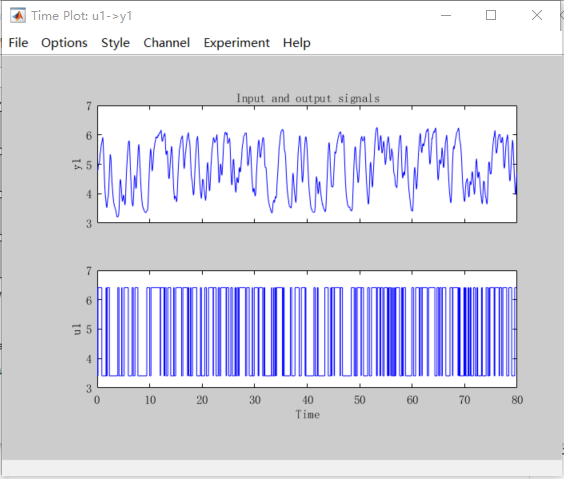
可以看到输入输出信号是有偏差的，点击GUI界面的preprocess（预处理）——>remove mean（移除平局值），可以得到偏差消除后的输出数据，此时的数据平均值为0，如下图所示。

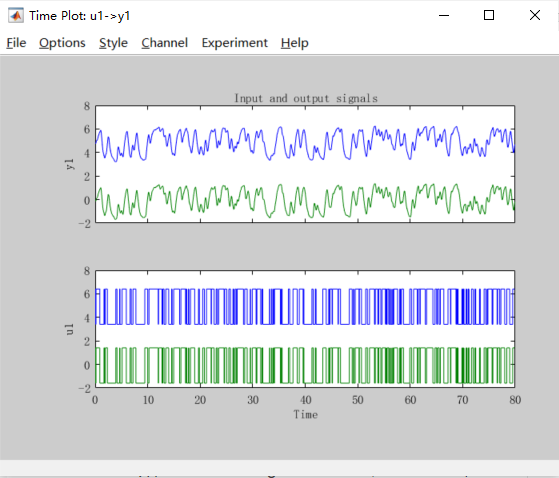
与此同时，在GUI 界面的数据方框中会出现一组datad 数据，将图框中的数据拖入Workingdata 方框中,如下图所示，此时数据处理的第一步已经完成。

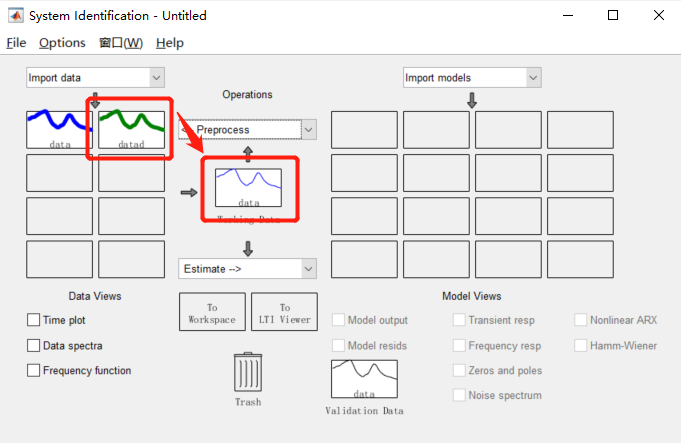
2.4 模型估计和验证

点击Estimate ——>polynomial models（多项式模型即线性模型）会弹出模型参数输入界面，在模型参数界面中
structure（结构）参数栏选择ARX:[na nb nk]；
orders（阶数）参数栏输入[1:10 1:10 1:10]【即模型三个变量的阶数为1～10阶】；
然后点击estimate 按钮弹出图6 所示的ARX 参数模型界面，其中红、蓝、绿三条是不同算法下的吻合度最高的模型。

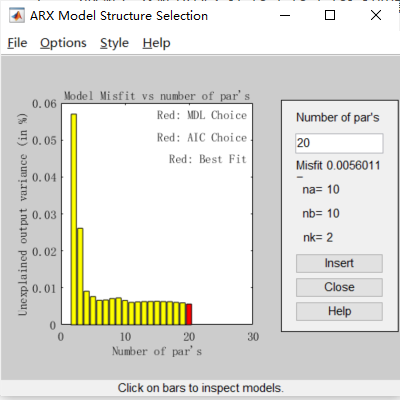
其中红色表示的是用最小二乘法得到的模型，它也是符合度最高的模型。
点击红色部分，然后点击insert按钮，模型就会自动加入GUI 界面的import models 中，然后勾选model output 框，就会弹出模型输出曲线界面，如下图所示，估计输出与验证数据输出重合度达到85.25%，说明估计模型比较符合实际。

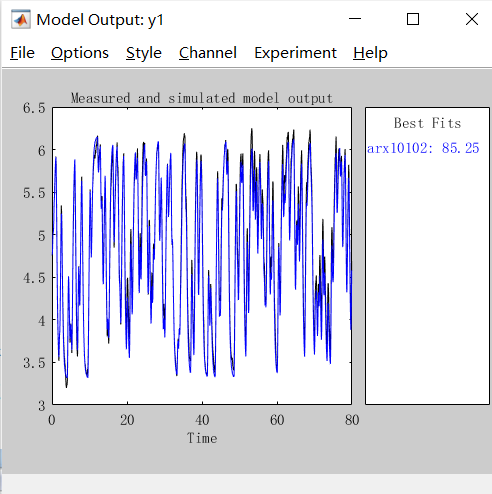
三、结论

本文主要讨论了MATLAB系统辨识仿真工具箱GUI 模块的系统辨识过程。通过工具箱GUI 模块可以非常方便地对“黑箱”系统进行系统识，不需要太多的编程，辨识的效率比较高。

参考：
1.《基于MATLAB 系统辨识工具的系统辨识》

最后

以上就是愉快老虎为你收集整理的MATLAB系统辨识工具箱介绍（完结）的全部内容，希望文章能够帮你解决MATLAB系统辨识工具箱介绍（完结）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。