Day16--S函数设计与应用

139 阅读 0 评论 92 点赞

我是靠谱客的博主聪慧飞鸟，这篇文章主要介绍Day16--S函数设计与应用，现在分享给大家，希望可以做个参考。

该系列博客主要讲述Matlab软件在自动控制方面的应用，如无自动控制理论基础，请先学习自动控制系列博文，该系列博客不再详细讲解自动控制理论知识。
自动控制理论基础相关链接：https://blog.csdn.net/qq_39032096/category_10287468.html?spm=1001.2014.3001.5482
博客参考书籍：《MATLAB/Simulink与控制系统仿真》。

4.综合实例

4.1 综合实例1

实验要求：给定 $RLC$ 网络，如下图所示，其中， $u_i(t)$ 为输入量， $u_o(t)$ 为输出量。求解此系统的传递函数模型、零极点增益模型、状态空间模型(假设 $R_1=1Omega，R_2=1Omega，C=1F，L=1H}$ )。

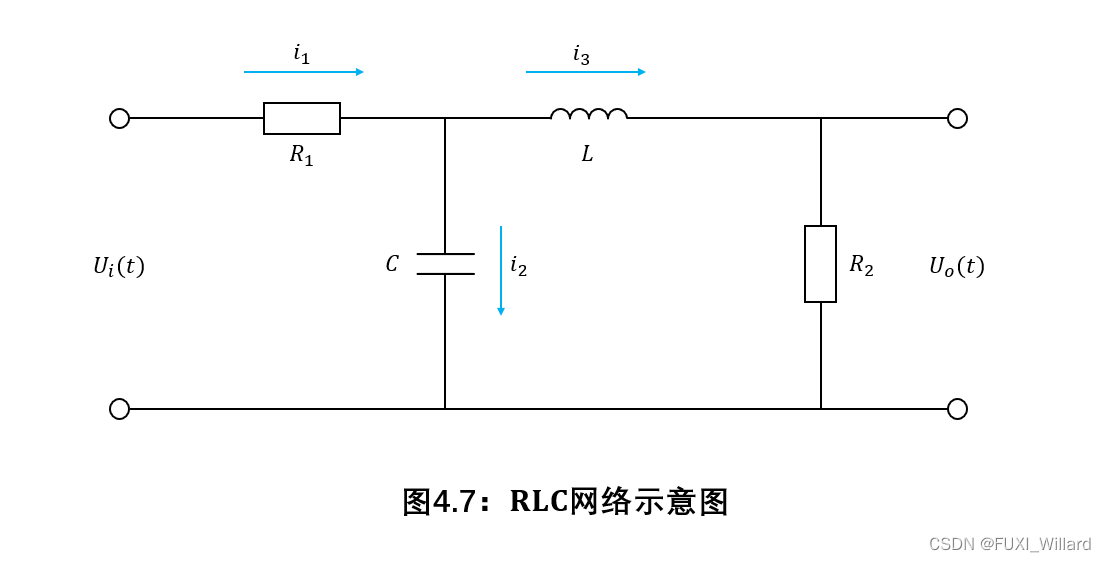
解：

【STEP1】：求解系统的传递函数。

根据电路的基本定理，结合 $RLC$ 网络示意图，列出该电路的微分方程，如下：
$&R_1i_1+Ldisplaystylefrac{{rm d}i_3}{{rm d}t}+u_o=u_i\\ &i_1=i_2+i_3，u_o=i_3R_2，i_2=Cdisplaystylefrac{{rm d}}{{rm d}t}left(Ldisplaystylefrac{{rm d}i_3}{{rm d}t}+u_oright) end{aligned}$
整理并化简上述方程，可得：
$frac{R_1CL}{R_2}frac{{rm d^2}u_o}{{rm d}t^2}+left(displaystylefrac{L}{R_2}+R_1Cright)displaystylefrac{{rm d}u_o}{{rm d}t}+left(1+displaystylefrac{R_1}{R_2}right)u_o=u_i$
在零初始条件下，对上式取拉普拉斯变换，整理可得：
$G(s)=frac{U_o(s)}{U_i(s)}=frac{1}{(R_1Cs+1)left(displaystylefrac{L}{R_2}s+1right)+displaystylefrac{R_1}{R_2}}$
代入具体数值 $R_1=1Omega，R_2=1Omega，C=1{rm F}，L=1{rm H}$ ，可得系统传递函数模型，有：
$G(s)=frac{1}{s^2+2s+2}$
【STEP2】：使用 $MATLAB$ 建立系统模型。

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
% 实例Chapter4.4 综合实例
clc;clear;

% 传递函数分子、分母多项式系数行向量
num=[0,1];den=[1,2,2];

% 建立传递函数模型
sys_tf=tf(num,den);

% 从传递函数模型获取系统的零极点增益
[z,p,k]=tf2zp(num,den);

% 建立系统的零极点增益模型
sys_zpk=zpk(z,p,k);

% 从零极点增益模型获取系统的状态空间模型
[A,B,C,D]=zp2ss(z,p,k);

% 建立系统的状态空间模型
sys_ss=ss(A,B,C,D);

% 显示模型
sys_tf,sys_zpk,sys_ss

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
% 结果显示：
% 传递函数模型
sys_tf = 
        1
  -------------
  s^2 + 2 s + 2 
Continuous-time transfer function.

% 零极点模型
sys_zpk = 
        1
  --------------
  (s^2 + 2s + 2) 
Continuous-time zero/pole/gain model.

% 状态空间模型
sys_ss = 
  A = 
           x1      x2
   x1      -2  -1.414
   x2   1.414       0
 
  B = 
       u1
   x1   1
   x2   0
 
  C = 
           x1      x2
   y1       0  0.7071
 
  D = 
       u1
   y1   0 
Continuous-time state-space model.

【STEP3】：求阶跃响应。

复制代码

1
2
3
4
5
6
7
% 求阶跃响应
step(sys_tf);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);

% 添加栅格
grid on;

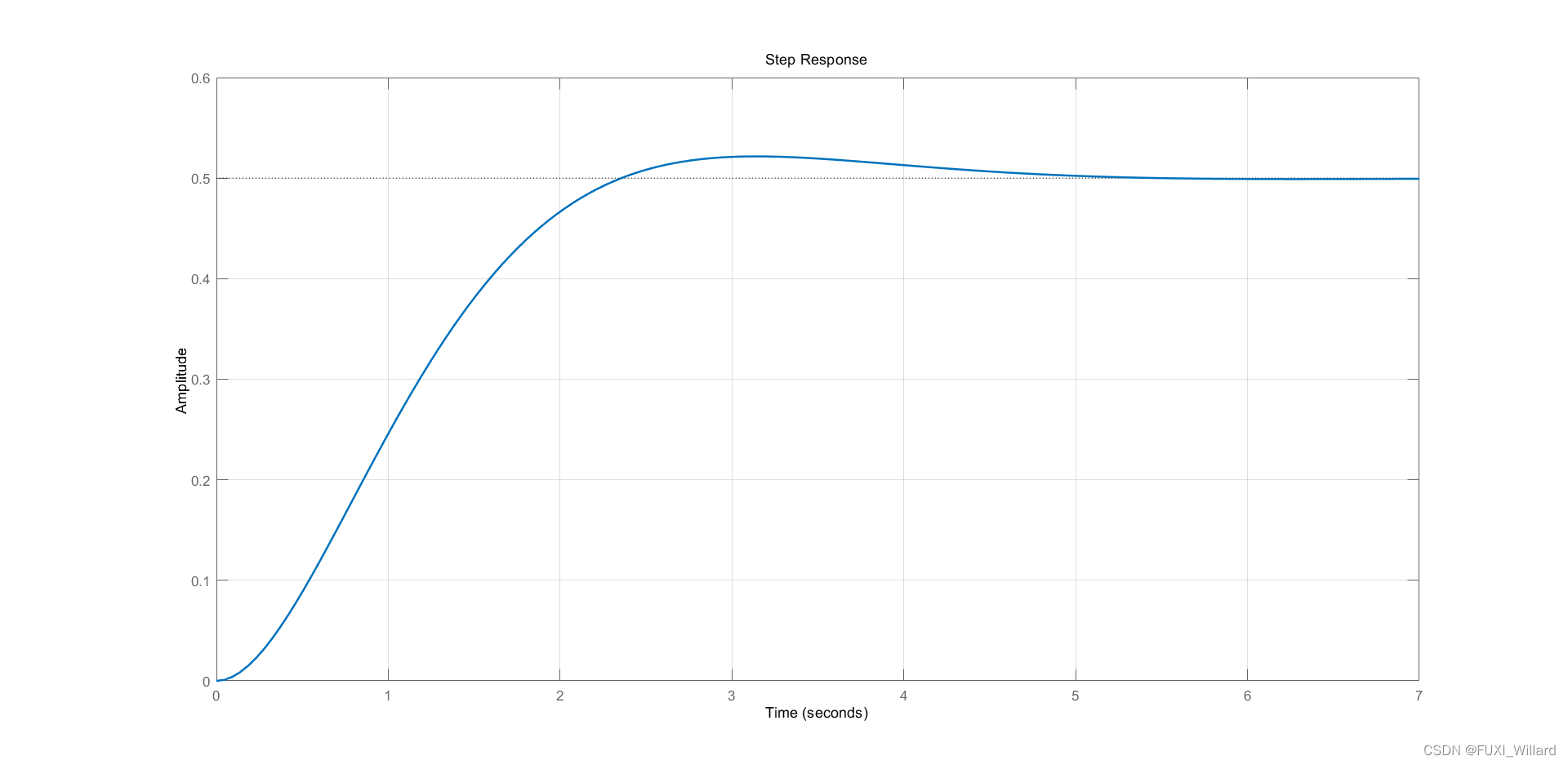
4.2 综合实例2

实验要求：已知某双环调速的电流环系统的结构如下图所示，采用 $SIMULINK$ 动态结构图求该系统线性模型。

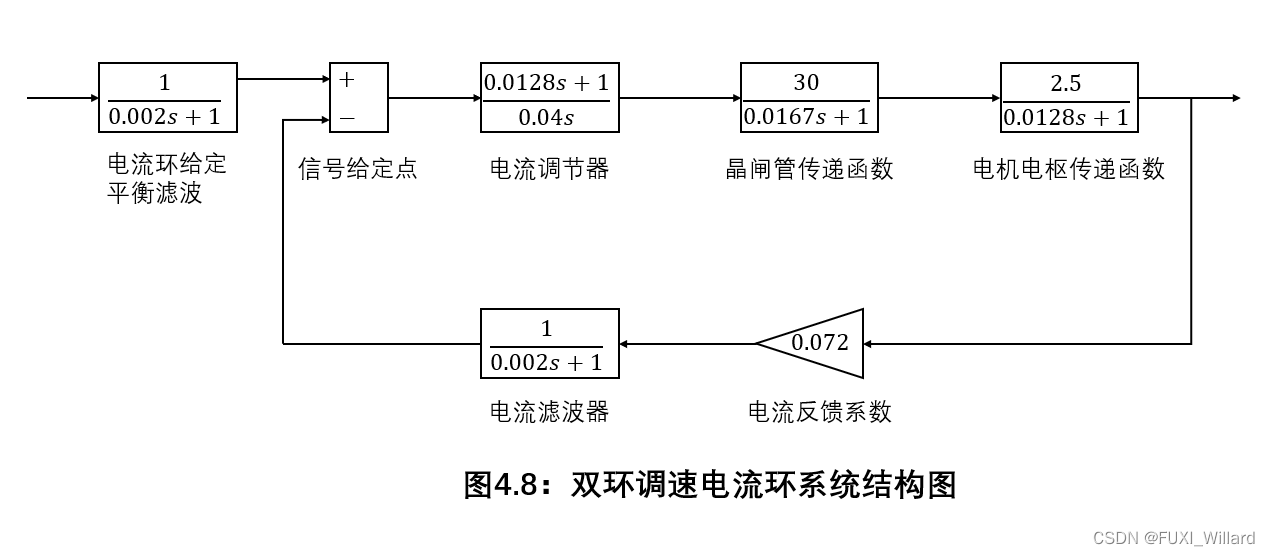
解：

【STEP1】：建立 $SIMULINK$ 动态结构图。

复制代码

1
2
3
# 1.把所需模块拖曳到模型窗口；
# 2.线连接起来，保存为"Experiment4_4_2.mdl"文件；

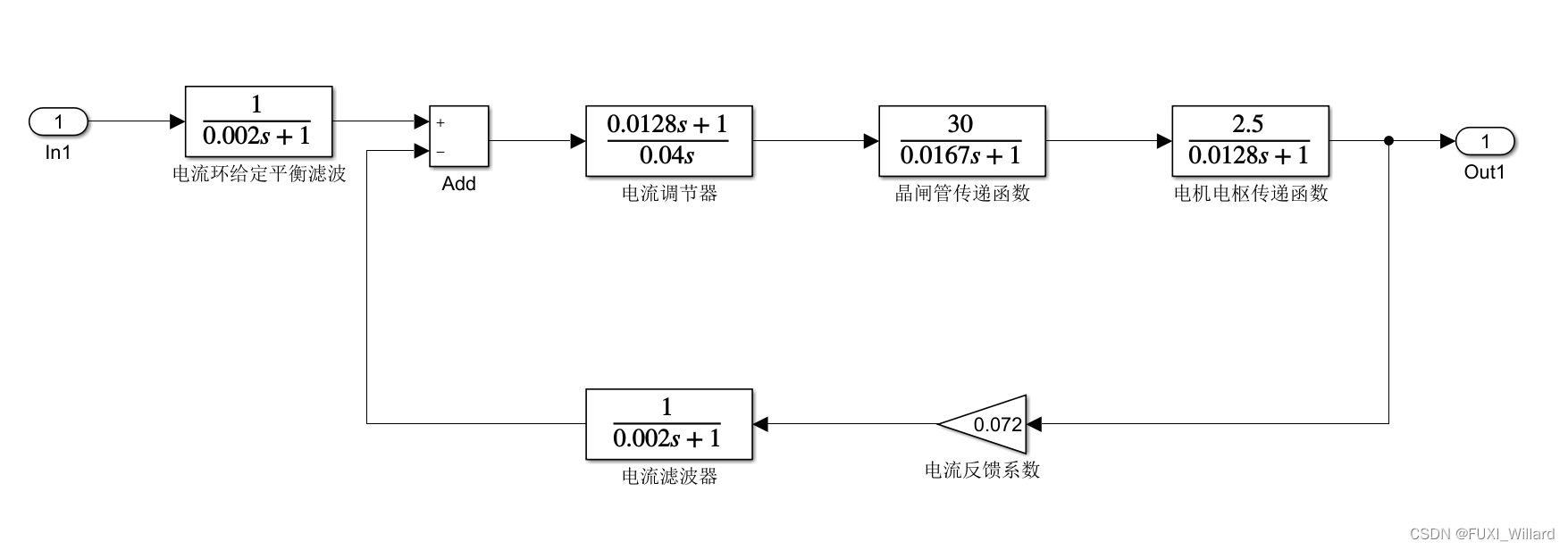
【STEP2】：求取系统的线性状态空间模型。

复制代码

1
2
3
% matlab命令行窗口下运行如下命令，得到一个线性状态空间模型
[A,B,C,D]=linmod('Experiment4_4_2')

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
% 结果显示：
A =
   1.0e+03 *

   -0.0781         0         0    1.7964         0
         0   -0.5000         0         0         0
    0.0141         0   -0.5000         0         0
         0    0.1600   -0.1600   -0.0599    0.0250
         0    0.5000   -0.5000         0         0

B =
     0
     1
     0
     0
     0

C =
  195.3125         0         0         0         0

D =
     0

【STEP3】：求系统的传递函数模型。

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
% 命令行窗口下
>> [num,den]=ss2tf(A,B,C,D);
>> printsys(num,den,'s');

% 结果显示：
num/den =  
             56137724.5509 s^2 + 32454622005.988 s + 2192879865269.461
   -----------------------------------------------------------------------------
   s^5 + 1138.0052 s^4 + 392683.3832 s^3 + 43221369.7605 s^2 + 3506268712.5748 s

   + 157887350299.401