python运用最小二乘法（scipy.optimize.leastsq）进行数据拟合与回归

拟合与回归

• 拟合：指把数据集按照其规律方程化的过程，拟合的方法很多。
• 回归：拟合的方法之一，有线性回归和非线性回归。当指线性回归时，即是求解最小二乘解。

最小二乘法（Leaest Square Method）

给定数据点集$(x_i,y_i),i\in (1,2,...,m)$

• 拟合函数$h(x)$
• 第$i$点数据点残差：$h(x_i)-y_i$
• 残差平方和: ${\sum }_1^m(h(x_i)-y_i{)}^2$

其中，$h(x)$为线性方程。假设$h(x)=k_0+k_{1}x$

• 平方损失函数：$Q(k)={\sum }_1^m(k_0+k_1{x}_i-y_i{)}^2$

至此， 最小二乘法就是要求解当$Q(k)$最小的情况下，$k_0$和$k_1$的值，从而求出拟合函数$h(x)=k_0+k_{1}x$。对未知数分别求偏导，令等式等于0，联立求解即可。

$$\begin{gathered} \frac{\partial Q}{\partial k_0}=2\sum _1^m(k_0+k_1{x}_i-y_i) \\ \frac{\partial Q}{\partial k_1}=2\sum _1^m(k_0+k_1{x}_i-y_i)x_i \end{gathered}$$

使用scripy.optimize的leastsq求解拟合方程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import numpy as np
from scipy.optimize import leastsq
"""target Func"""
def real_func(x):
    return np.sin(2 * np.pi * x)
"""gen polynomial func"""
def fit_func(p, x):
    f = np.poly1d(p)
    return f(x)
 """残差函数"""
def error_func(p, y ,x):
    ret = fit_func(p, x) - y
    return ret

x = np.linspace(0, 1, 9) ##在0~1生成等间距的9个数
x_point = np.linspace(0, 1, 1000) ##为了图形的连续性，画图的点要尽可能多

y0 = real_func(x) ## 生成xi对应的yi
y1 = [np.random.normal(0, 0.1) + y for y in y0] ##生成均值为为0方差为1的正态分布数并返回一个值作为噪声加入 

n = 9
p_init = np.random.randn(n)
plsq = leastsq(error_func, p_init, args=(y1, x))

plt.plot(x_point, real_func(x_point), label='real')
plt.plot(x_point, fit_func(plsq[0], x_point), label='fitted curve')
plt.plot(x, y1, 'bo', label='with noise')
plt.legend()
plt.show()

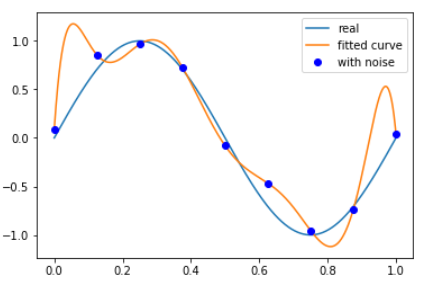
• 拟合结果跟原函数有所偏差，原因是由于在原数据中加入了噪声干扰，导致了过拟合(overfitting)。过拟合会导致模型失去或大大降低预测能力。

• 纠正过拟合：在模型中加入惩罚项，常用L1正则化或L2正则化，并且给惩罚项乘以一个常数，作为惩罚系数，以表示惩罚项的权重大小。即损失函数改写为：$$Q(k)=\sum _1^m(k_0+k_1{x}_i-y_i{)}^2+\lambda ||w|{|}^2$$

  • L1正则化（L1范数）： 拟合函数所有参数之和
  • L2正则化（L2范数）： 拟合函数所有参数的平方和

• 在本例中以L2正则化作为惩罚项， 即残差函数改为

  复制代码def error_func(p, y ,x): ret = fit_func(p, x) - y ret = np.append(ret, np.sqrt(0.0001) * p) return ret

  1
  2
  3
  4
  5
  def error_func(p, y ,x):
      ret = fit_func(p, x) - y
      ret = np.append(ret, np.sqrt(0.0001) * p)
      return ret
  

  其中，惩罚系数为0.01， 拟合情况为：
  

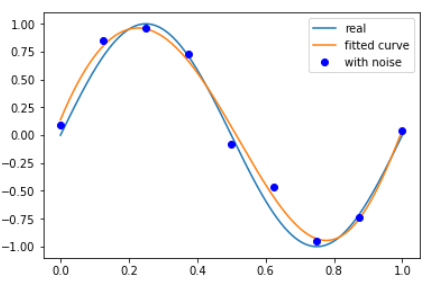
• 若惩罚系数过大，会出现欠拟合(underfitting)。欠拟合无法正确反映数据特征。

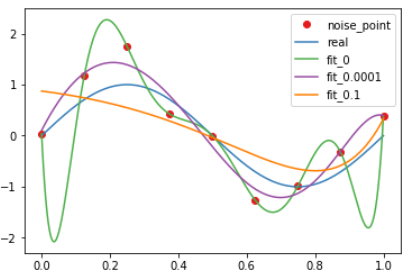
• 以下分别为惩罚系数数为0.1和1的情况
  
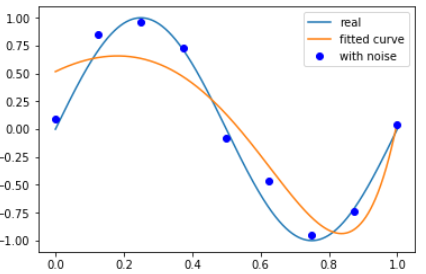
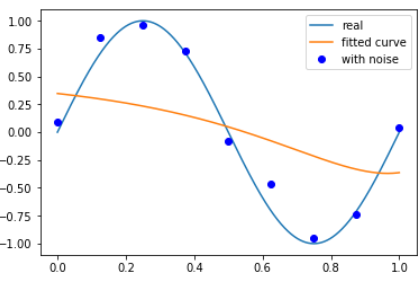
  增大噪声，改变惩罚项系数，可以看到结果较为明显：
  

最后

以上就是欣喜豌豆最近收集整理的关于python运用最小二乘法（scipy.optimize.leastsq）进行数据拟合与回归的全部内容，更多相关python运用最小二乘法（scipy内容请搜索靠谱客的其他文章。