最近做的课题需要求解方程组，方程组还挺复杂，未知参数比较多

简单粗暴介绍fsolve()函数用法：

假如要解方程组
x*y=6
x+y=5

先变换成右边为0的形式
x*y-6
x+y-5

func函数中直接替换要解的方程就可

import scipy
from scipy.optimize import fsolve

def func(i):
    x, y = i[0], i[1]
    return [  # 这里写要求解的方程组式子，变成等于0的形式
        x*y-6,
        x+y-5 ]

if __name__ == '__main__':
    r = scipy.optimize.fsolve(func, [0, 0])
    print(r)

结果

[2. 3.]

再看看有参数的解法：

如果有参数a,b需要传入
axy-6
x+by-5

import scipy
from scipy.optimize import fsolve

def func(i, params):
    x, y = i[0], i[1]
    a, b = params
    return [  # 这里写要求解的方程组式子，变成等于0的形式
        a*x*y-6,
        x+b*y-5 ]
if __name__ == '__main__':
    a = 2
    b = 0.5
    params = [a, b]
    r = scipy.optimize.fsolve(func, [0, 0], args=params)
    print(r)

结果

[0.32055053 9.35889894]

近似解

更复杂的方程式带有循环求和：

附三角函数写法

import math
math.sin(theta)

带求和符号的方程求解（这里举一个简单的例子好理解一些）

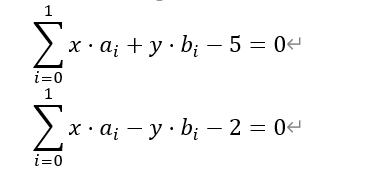
这里用sum来计算和

import scipy
from scipy.optimize import fsolve

def func(i, params):
    x, y = i[0], i[1]
    a, b = params
    list_e1 = [x * a[j][0] + y * b[j][0] - 5 for j in range(2)]
    list_e2 = [x * a[j][1] - y * b[j][1] - 2 for j in range(2)]
    return [  # 这里写要求解的方程组式子，变成等于0的形式
        sum(list_e1),
        sum(list_e2)
    ]

if __name__ == '__main__':
    a = [[3, 4], [3, 4]]
    b = [[1, 3], [4, 1]]
    params = [a, b]
    r = scipy.optimize.fsolve(func, [0, 0], args=params)
    print(r)

结果

[0.9375 0.875 ]

最后

以上就是安静仙人掌为你收集整理的Python解方程组 scipy.optimize.fsolve()函数 求解带有循环求和的方程式简单粗暴介绍fsolve()函数用法：再看看有参数的解法：更复杂的方程式带有循环求和：的全部内容，希望文章能够帮你解决Python解方程组 scipy.optimize.fsolve()函数 求解带有循环求和的方程式简单粗暴介绍fsolve()函数用法：再看看有参数的解法：更复杂的方程式带有循环求和：所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。