一、正则化之weight_decay
1、Regularization:减少方差的策略
误差可分解为:偏差、方差与噪声之和。
误差=偏差+方差+噪声
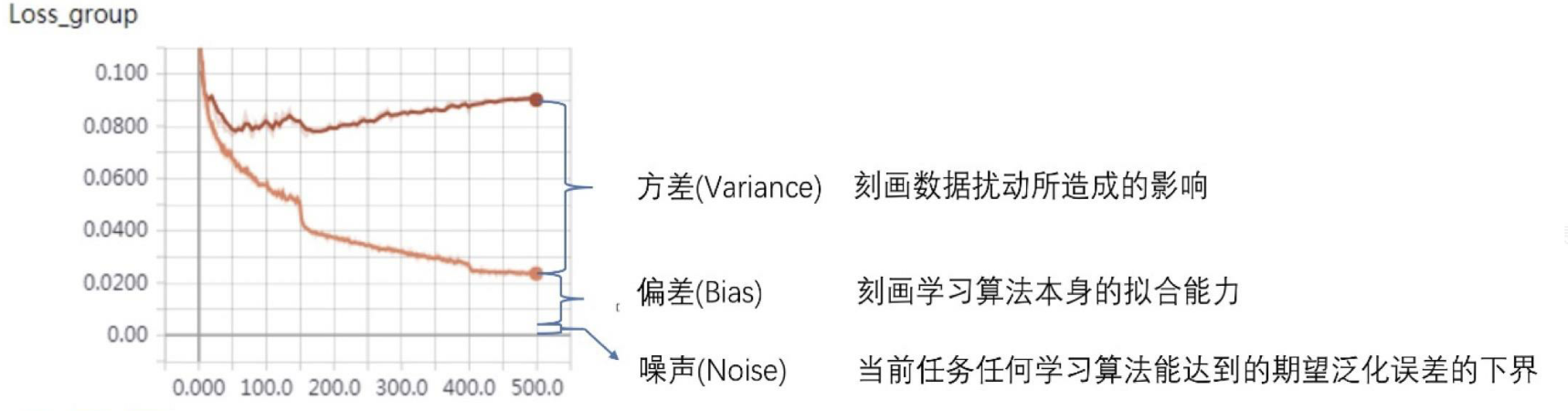
偏差:度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力;
方差:度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响;
噪声:表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界;
损失函数:衡量模型输出与真实标签的差异;
损失函数(loss function):
代价函数(cost function):
目标函数(objective function):
obj = Cost + Regularization Term
针对Regularization Term常用的有两种:
- L1 Regularization Term
- L2 Regularization Term
(1) L1 Regularization Term
(2)L2 Regularization Term
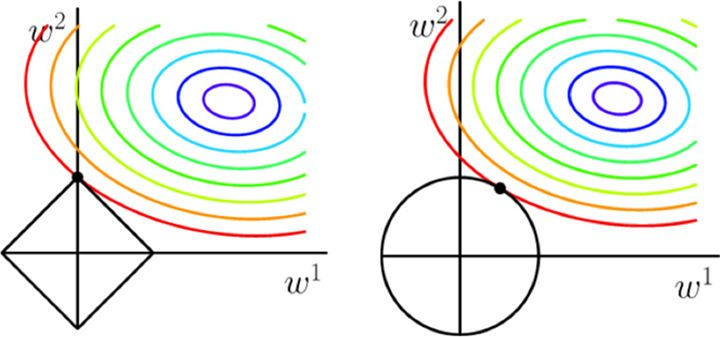
左边的图对应L1正则化,右边对应L2正则化;
regularization解决overfitting(L2正则化解决过拟合问题)
regularization可以使得训练曲线变得更加平缓,在训练集上的误差变大,但是在测试集上的误差变小。
最初的loss function只是考虑了prediction的error,而regularization是在原来loss function的基础上加了一个正则化项,就是上面对应的L1和L2;

针对增加的正则化项,其中主要有两个参数, 和
, 因此就期望参数
的值越小甚至接近0;因为参数值接近0的function是比较平滑的,这里为什么没有考虑偏置
呢?因为这个参数值大小与function的平滑程度是没有关系的,偏置的大小只是把function上下移动而已;针对较平滑的function,由于输出对输入是不敏感的,测试的时候,一些噪声对这个平滑的function的影响就会较小。
还有就是 这个值是需要手动去调整以取得最好的值;具体可以参考李宏毅老师的讲解:
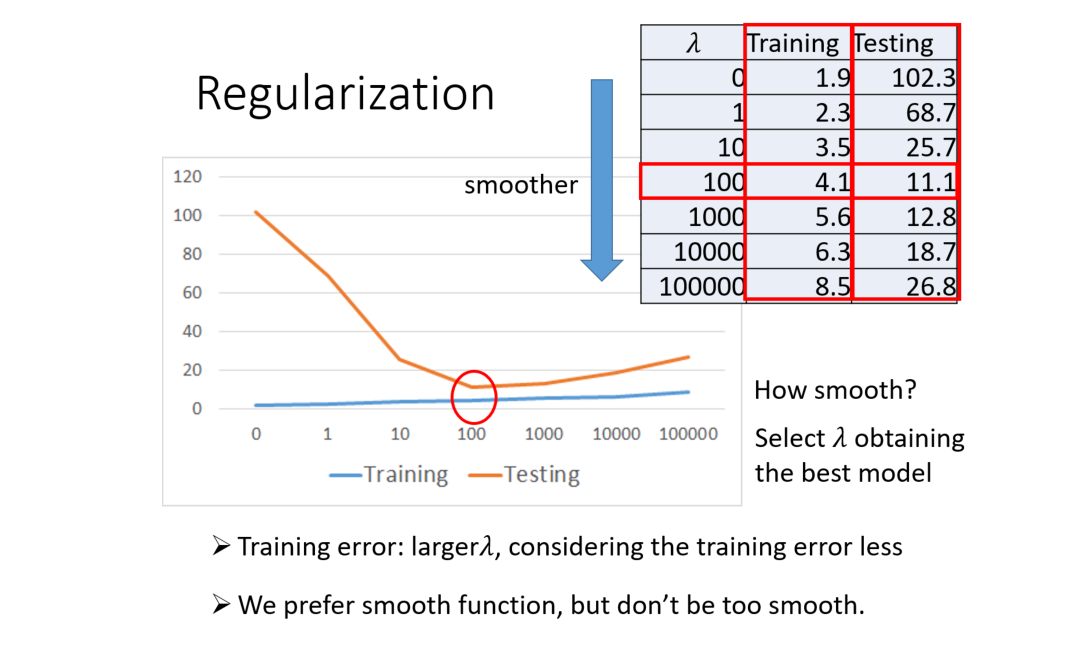
我们喜欢比较平滑的function,因为它对noise不那么sensitive;但是我们又不喜欢太平滑的function,因为它就失去了对data拟合的能力;而function的平滑程度,就需要通过调整 来决定;

L2 Regularization = weight decay(权值衰减)

代码部分:
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from tools.common_tools import set_seed
from torch.utils.tensorboard import SummaryWriter
set_seed(1)
n_hidden = 200
max_iter = 2000
disp_interval = 200
lr_init = 0.01
def gen_data(num_data=10, x_range=(-1, 1)):
w = 1.5
train_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
train_y = w*train_x + torch.normal(0, 0.5, size=train_x.size())
test_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
test_y = w*test_x + torch.normal(0, 0.3, size=test_x.size())
return train_x, train_y, test_x, test_y
train_x, train_y, test_x, test_y = gen_data(x_range=(-1, 1))
class MLP(nn.Module):
def __init__(self, neural_num):
super(MLP, self).__init__()
self.linears = nn.Sequential(
nn.Linear(1, neural_num),
nn.ReLU(inplace=True),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Linear(neural_num, 1),
)
def forward(self, x):
return self.linears(x)
net_normal = MLP(neural_num=n_hidden)
net_weight_decay = MLP(neural_num=n_hidden)
# 优化器
optim_normal = torch.optim.SGD(net_normal.parameters(), lr=lr_init, momentum=0.9)
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)
# 损失函数
loss_func = torch.nn.MSELoss()
writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")
for epoch in range(max_iter):
# forward
pred_normal, pred_wdecay = net_normal(train_x), net_weight_decay(train_x)
loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)
optim_normal.zero_grad()
optim_wdecay.zero_grad()
loss_normal.backward()
loss_wdecay.backward()
optim_normal.step()
optim_wdecay.step()
if (epoch+1) % disp_interval == 0:
# 可视化
for name, layer in net_normal.named_parameters():
writer.add_histogram(name + '_grad_normal', layer.grad, epoch)
writer.add_histogram(name + '_data_normal', layer, epoch)
for name, layer in net_weight_decay.named_parameters():
writer.add_histogram(name + '_grad_weight_decay', layer.grad, epoch)
writer.add_histogram(name + '_data_weight_decay', layer, epoch)
test_pred_normal, test_pred_wdecay = net_normal(test_x), net_weight_decay(test_x)
# 绘图
plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')
plt.plot(test_x.data.numpy(), test_pred_normal.data.numpy(), 'r-', lw=3, label='no weight decay')
plt.plot(test_x.data.numpy(), test_pred_wdecay.data.numpy(), 'b--', lw=3, label='weight decay')
plt.text(-0.25, -1.5, 'no weight decay loss={:.6f}'.format(loss_normal.item()), fontdict={'size': 15, 'color': 'red'})
plt.text(-0.25, -2, 'weight decay loss={:.6f}'.format(loss_wdecay.item()), fontdict={'size': 15, 'color': 'red'})
plt.ylim((-2.5, 2.5))
plt.legend(loc='upper left')
plt.title("Epoch: {}".format(epoch+1))
plt.show()
plt.close()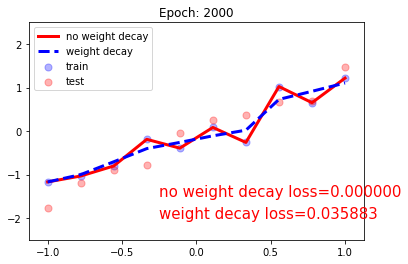
虽然no weight decay拟合了所有的点,但是过拟合了,我们需要的是平滑的;
最后
以上就是虚拟招牌最近收集整理的关于正则化之weight-decay的全部内容,更多相关正则化之weight-decay内容请搜索靠谱客的其他文章。








发表评论 取消回复