0. 简介

这篇SLAM论文《Direct LiDAR Odometry: Fast Localization with Dense Point Clouds》作为NASA喷气推进实验室CoSTAR团队研究和开发的新作，收到了学术界广泛的关注。其主要用作DARPA地下挑战的里程计，提出了一种能够实现高速高精度处理高速实时处理密集点云的激光里程计(LO)的思路，下面是他们的Github开源代码。

1. 文章贡献

文中提出了一种轻量前端激光雷达里程计解决方案，用于在计算能力受限的机器人平台上，具有快速和精确的定位能力，我们的直接激光雷达里程计（DLO）方法包括几个关键的算法上的创新，这些创新优先考虑计算效率，并使用稠密的、预处理最少的点云实时提供准确的姿势估计。以下是文章的主要创新点：

1. 提出了一个定制的速度优先的处理流程，这个流程可以实时精确的估计位姿，对预处理的需求比较小，并且IMU是可选项。
2. 提出了一个新的关键帧系统，可以根据环境信号自适应的选择关键帧，并且可以通过凸优化快速的生成子图。
3. 从实验中发展出几个重要的算法见解，以进一步降低计算开销，从而产生了NanoGICP(定制的迭代最接近点解算器，用于轻量级点云扫描与交叉对象数据共享匹配)。

下图展示了该激光雷达里程计应用的两个计算资源有限的机器人平台（A） 定制的四旋翼平台，顶部有一个驱逐OS1激光雷达传感器。（B） Boston Dynamics Spot机器人，装有负载和带防护装置的Velodyne VLP-16。（C） 使用我们的轻型里程计方法在这些机器人上绘制的石矿的俯视图

2. 整体思路

整个系统是通过RANSAC排除离群点和用IMU来获得旋转先验，然后获得帧到帧的相对位姿。这个相对位姿之后传播到世界坐标系，并且用于二级GICP的初始化值。

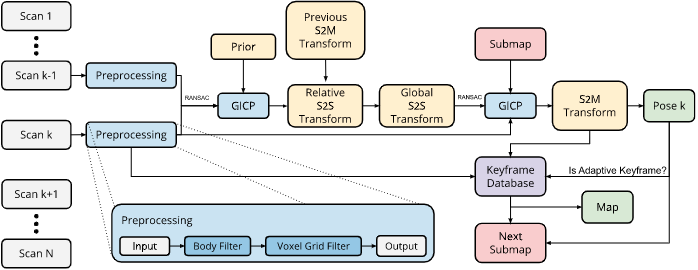
2.1 预处理

在预处理过程中只使用了两个滤波器：首先，通过原点周围大小为1立方米的盒子滤波器删除机器人自身可能返回的所有点云。然后，生成的点云通过分辨率为0.25m的三维体素网格滤波器发送，以便在保持周围环境中的主要结构的同时，略微减少后续任务的数据采样。在这项工作中，我们不校正运动失真，因为非刚性变换可能会带来计算负担，我们直接使用稠密点云，而不是提取特征，平均而言，每帧点云包含了预处理后得到1000点。

2.2 基于GICP(Generalized-ICP)的位姿计算

这部分分成了两步，第一步是提供瞬时的位姿估计(帧间位姿), 第二步是提供优化的位姿(帧图优化)。这部分也就是下文最后提到的NanoGICP高效匹配。为了促进点云扫描与交叉对象数据共享匹配，文中提出开发了NanoGICP，这是一个自定义迭代最近点解算器，本质上是将开源的FastGICP和NanoFLANN两个包进行合并，使用NanoGICP的NanoFLANN来高效构建KD-tree, 然后通过FastGICP进行高效匹配。

A. 帧间匹配

基于激光雷达的里程计可被视为通过比较连续点云和内存中的点云来恢复SE（3）变换来解析机器人自我运动的过程。此过程通常分两个阶段运行，首先是提供最佳初始值，随后将其优化为与先前关键帧位置保持其全局一致。

目标函数为下式，其中${\hat{\mathbf{X}}}_k^{\mathcal{L}}$代表了在$s$时刻和$t$时刻的位姿相对变换，${\mathcal{P}}_k^{\mathrm{s}}$代表了source的扫描的点云，${\mathcal{P}}_k^{\mathrm{t}}$代表了target的扫描的点云(${\mathcal{P}}_k^{\mathrm{t}}={\mathcal{P}}_{k-1}^{\mathrm{s}}$这代表了$k$时刻的target点云与$k-1$时刻的source点云)。

$${\hat{\mathbf{X}}}_k^{\mathcal{L}}=\underset{{\mathbf{x}}_k^{\mathcal{L}}}{\mathrm{argmin}}\mathcal{E}\left({\mathbf{X}}_k^{\mathcal{L}}{\mathcal{P}}_k^{\mathrm{s}},{\mathcal{P}}_k^{\mathrm{t}}\right)$$

其中$\mathcal{E}$为误差函数，这里被定义为:

$$\begin{gathered} \mathcal{E}\left({\mathbf{X}}_k^{\mathcal{L}}{\mathcal{P}}_k^{\mathrm{s}},{\mathcal{P}}_k^{\mathrm{t}}\right)=\sum _i^N{d}_i^{\mathrm{T}}{\left({\mathcal{C}}_{k,i}^{\mathrm{t}}+{\mathbf{X}}_k^{\mathcal{C}}{\mathcal{C}}_{k,i}^{\mathrm{s}}{\mathbf{X}}_k^{\mathcal{L}}\right)}^{-1}{d}_i \\ {d}_i=p_i^t-{\mathbf{X}}_k^L{p}_i^{\mathrm{s}},p_i^{\mathrm{s}}\in {\mathcal{P}}_k^{\mathrm{s}},p_i^{\mathrm{t}}\in {\mathcal{P}}_k^{\mathrm{t}} \end{gathered}$$

其中$d_i=p_i^t-{\mathbf{X}}_k^{\mathcal{L}}{p}_i^s，p_i^t\in {\mathcal{P}}_k^{\mathrm{t}},p_i^s\in {\mathcal{P}}_k^{\mathrm{s}}$表示了点云中的两个点的距离差。${\mathcal{C}}_{k,i}^{\mathrm{s}},{\mathcal{C}}_{k,i}^{\mathrm{t}}$指的是两个点云中每个点$i$对应的估计协方差矩阵。

B. 帧图匹配

…详情请参照古月居

最后

以上就是从容纸鹤为你收集整理的经典文献阅读之--DLO0. 简介1. 文章贡献2. 整体思路的全部内容，希望文章能够帮你解决经典文献阅读之--DLO0. 简介1. 文章贡献2. 整体思路所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。