项目背景:
对图像的感兴趣区域进行描绘出封闭曲线,并获得其面积、长轴短轴的长度信息,同时支持新增封闭曲线上点,对点进行拖动,可扩大曲线和缩小曲线,且在拖动点的过程中,拖动点在某点的靠近远端或者近端,则被靠点会被淹没,如果靠近某点,则对拖动点进行切换。
项目思路:
1.获取到采样离散点,采用贝塞尔曲线实现基础封闭曲线;
2.获得曲线上的点集合,采用Opencv的contourArea函数求取面积;采用fitEllipse获取其中心点。
3.新增点时,1>判定点在曲线上,2>新增点放置在正确的位置,即QVector的点顺序。
4.拖动点时,判断该点和中心点的一定夹角内,是否涵盖了已有的离散点,如果有则将其淹没。
5.拖动点时,判断该点和其他离散点是否在其设定的覆盖范围内,若是则进行拖动点的切换,在选定拖动点时,则需要记录即将要拖动的点。
实现方案:
1.绘制封闭曲线:
查找贝塞尔曲线实现封闭曲线的可用源码,可参考:
(2条消息) 根据多个点绘制闭合的曲线_飞天_的博客-CSDN博客_给定若干点生成曲线
http://t.csdn.cn/kKskO http://t.csdn.cn/kKskO该博文实现离散点闭合曲线,可用。在拖动封闭曲线上点往远离中心点的过程中,临近的点所形成的曲线会往相反方向上移动,贝塞尔曲线的控制点外扩所致,体验不好。因此尝试适用b样条拟合封闭曲线,相对贝塞尔曲线(本文实现)而言,b样条的拖动效果更为符合项目需求,可参考博文:
http://t.csdn.cn/kKskO该博文实现离散点闭合曲线,可用。在拖动封闭曲线上点往远离中心点的过程中,临近的点所形成的曲线会往相反方向上移动,贝塞尔曲线的控制点外扩所致,体验不好。因此尝试适用b样条拟合封闭曲线,相对贝塞尔曲线(本文实现)而言,b样条的拖动效果更为符合项目需求,可参考博文:
(2条消息) 三次B样条曲线插值c++_cnmgbmsdn的博客-CSDN博客_c++ 曲面插值
/*
通过离散点集反求控制点
*/
vector<Point2f> BSplineInterpolate(vector<Point2f> discretePoints) {
int N = discretePoints.size();
Mat weight = Mat::zeros(Size(N,N), CV_32F);
for (int i = 0; i < weight.rows; i++) {
weight.ptr<float>(i)[i] = 1;
weight.ptr<float>(i)[(i+1)%weight.cols] = 4;
weight.ptr<float>(i)[(i+2)%weight.cols] = 1;
}
Mat V = Mat::zeros(Size(2, N), CV_32F);
float* vdata = (float*)V.data;
int idx = 0;
for_each(discretePoints.begin(), discretePoints.end(), [&vdata, &idx](Point2f p2f) {vdata[idx++] = p2f.x; vdata[idx++] = p2f.y; });
V *= 6;
Mat P = weight.inv()*V;
vector<Point2f> res(discretePoints.size());
float* pdata = (float*)P.data;
idx = 0;
for_each(res.begin(), res.end(), [&idx, pdata](Point2f& p2f) {p2f.x = pdata[idx++]; p2f.y=pdata[idx++]; });
return res;
}
————————————————
版权声明:本文为CSDN博主「cnmgbmsdn」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/cnmgbmsdn/article/details/108188007/*B样条曲线拟合
@return 返回拟合得到的曲线
@discretePoints 输入的离散点,至少4个点
@closed 是否拟合闭合曲线,true表示闭合,false不闭合
@stride 拟合精度
*/
vector<Point2f> BSplineFit(vector<Point2f> discretePoints, bool closed, double stride) {
vector<Point2f> fittingPoints;
for (int i = 0; i < (closed ? discretePoints.size() : discretePoints.size() - 1); i++) {
Point2f xy[4];
xy[0] = (discretePoints[i] + 4 * discretePoints[(i + 1) % discretePoints.size()] + discretePoints[(i + 2) % discretePoints.size()]) / 6;
xy[1] = -(discretePoints[i] - discretePoints[(i + 2) % discretePoints.size()]) / 2;
xy[2] = (discretePoints[i] - 2 * discretePoints[(i + 1) % discretePoints.size()] + discretePoints[(i + 2) % discretePoints.size()]) / 2;
xy[3] = -(discretePoints[i] - 3 * discretePoints[(i + 1) % discretePoints.size()] + 3 * discretePoints[(i + 2) % discretePoints.size()] - discretePoints[(i + 3) % discretePoints.size()]) / 6;
for (double t = 0; t <= 1; t += stride) {
Point2f totalPoints = Point2f(0, 0);
for (int j = 0; j < 4; j++) {
totalPoints += xy[j] * pow(t, j);
}
fittingPoints.push_back(totalPoints);
}
}
return fittingPoints;
}
————————————————
版权声明:本文为CSDN博主「cnmgbmsdn」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/cnmgbmsdn/article/details/1081880072.计算长轴和短轴:采用fitEllipse得到拟合的椭圆cv::RotatedRect,根据中心点和Ellipse的宽高和角度得到长轴和短轴的坐标点,但是得到的点有时候不在贝塞尔曲线上,无法满足要求,原因是贝塞尔曲线点得到的拟合圆已经脱离了曲线本身。
考虑到长轴或者短轴,经过中心点,则计算得到最小和最大的距离点,并和中心点组合一条直线,该直线定会和曲线上相交,从而得到长轴或短轴对应的另外一点。计算过程中要排除自身点的影响。
另外一点计算策略为:根据直线的斜率判断,已知点和中心点,另一点和中心点所计算得到的斜率差值最小,则为长轴或者短轴上另外一点。
3.新增点,如何把点放置于在QVector中正确定顺序。假设存在n个点Pi(i=0,1,2...n-1),在第n和第n+1个点所形成的曲线中新增一个点,则对应也要将该点放置于第n+1点的点序上。判定策略为计算夹角,第n点、第n+1点和中心点所形成的夹角为新增点分别和第n点和第n+1点。
实现效果:
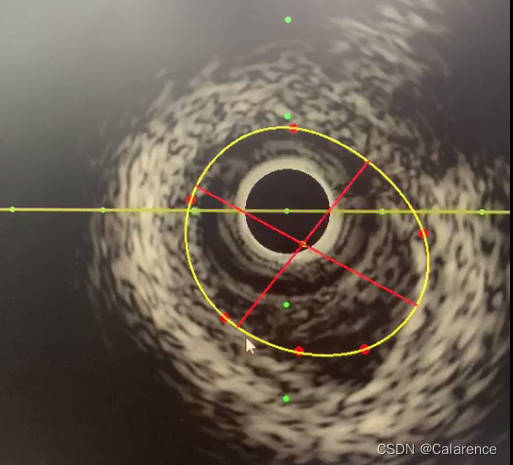
最后
以上就是糟糕音响最近收集整理的关于C++实现不规则封闭曲线绘制、面积、长短轴计算方案总结(一)的全部内容,更多相关C++实现不规则封闭曲线绘制、面积、长短轴计算方案总结(一)内容请搜索靠谱客的其他文章。








发表评论 取消回复