分类与预测算法评价
Kappa统计
Kappa统计是比较两个或多个观测者对同一事物,或观测者对同一事物的两次或多次观测结果是否一致,以由于机遇造成的一致性和实际观测的一致性之间的差别大小作为评价基础的统计指标。Kappa统计量和加权Kappa统计量不仅可以用于无序和有序分类变量资料的一致性、重现性检验,而且能给出一个反映一致性大小的“量”值。
- Kappa = +1:说明两次判断的结果完全一致
- Kappa = -1 :说明两次判断的结果完全不一致
- Kappa = 0 :说明两次判断的结果是机遇造成
- Kappa < 0:说明一致程度比机遇造成的还差,两次检查结果很不一致,在实际应用中无意义
- Kappa > 0:此时说明有意义,Kappa越大,说明一致性越好
- Kappa >= 0.75:说明已经取得相当满意的一致程度
- Kappa < 0.4:说明一致程度不够
识别准确度
| - | True | False |
|---|---|---|
| Positive | TP | FP |
| Negative | TN | FN |
预测正确的个数:
Accuracy = T P + T N T P + T N + F P + F N × 100 % frac{TP+TN}{TP+TN+FP+FN} × 100% TP+TN+FP+FNTP+TN×100%
识别准确率
Precision = T P T P + T N × 100 % frac{TP}{TP+TN} × 100% TP+TNTP×100%
反馈率
Recall = T P T P + F N × 100 % frac{TP}{TP+FN} × 100% TP+FNTP×100%
ROC曲线
受试者工作特性(Receiver Operationg Characteristic, ROC)曲线是一种非常有效的模型评价方法,可为选定临界值给出定量提示。
- 纵轴:灵敏度(Sensitivity)
- 横轴:1-特异性(1-Specificity)
- 曲线面积:反映分类器正确分类的统计概率,越接近1说明算法效果越好
混淆矩阵
混淆矩阵(Confusion Matrix,描绘样本数据的真实属性与识别结果类型之间的关系,是评价分类器性能的一种常用方法。
对于一个二分类预测模型,分类结束后的混淆矩阵:

如有150个样本数据,这些数据分成3类,每类50个。分类结束后得到的混淆矩阵如下:
| 43 | 5 | 2 |
|---|---|---|
| 2 | 45 | 3 |
| 0 | 1 | 49 |
第一行的数据说明有43个样本正确分类,有5个样本应该属于第1类,却错误分到了第2类,有2个样本应属于第1类,却错误分到了第3类。
5.2 聚类分析
与分类不同,聚类分析是在没有给定划分类别的情况下,根据数据相似度进行样本分组的一种方法,建立在无类标记的数据上,是一种非监督的学习算法。聚类的输入是一组未被标记的样本,聚类根据数据自身的距离或相似度将其划分为若干组,划分的原则是组内距离最小化而组间(外部)距离最大化。
常用聚类算法:
| 算法名称 | 算法描述 |
|---|---|
| K-Means | K-均值聚类也称为快速聚类法,在最小化误差函数的基础上将数据划分为预定的类数K,该算法原理简单并便于处理大量数据 |
| K-中心点 | K-均值算法对孤立点的敏感性,K-中心点算法不采用簇中对象的平均值作为簇中心,而选用簇中离平均值最近的对象最为簇中心 |
| 系统聚类 | 也称为多层次聚类,分类的单位由高到低呈树形结构,且所处的位置越低,其所包含的对象就越少,但这些对象间的共同特征越多。该聚类方法只适合在小数据量的时候使用,数据量大的时候速度会非常慢 |
5.2.1 K-Means聚类算法
K-Means算法是典型的基于距离的非层次聚类算法,采用距离作为相似性的评价指标,两个对象的距离越近,其相似度就越大。
算法过程:
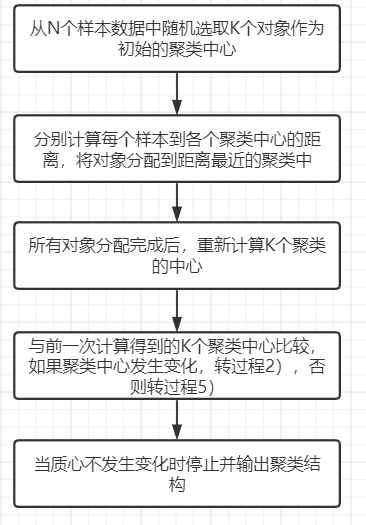
聚类的结果可能依赖于初始聚类中心的随机选择,可能使得结果严重偏离全局最优分类。实践中,为了得到较好的结果,通常选择不同的初始聚类中心,多次运行K-Means算法。在所有对象分配完成后,重新计算K个聚类的中心时,对于连续数据,聚类中心取该簇的均值;但当样本的某些属性是分类属性时,均值可能无定义,可以使用K-众数方法。
#聚类分析
import pandas as pd
inputfile = 'G:/Python数据分析与挖掘实战/chapter5/demo/data/consumption_data.xls' #销量及其他属性数据
outputfile = 'G:/Python数据分析与挖掘实战/chapter5/zl/data_type.xlsx' #保存结果的文件名
k = 3 #聚类的类别
iteration = 500 #聚类的最大循环次数
data = pd.read_excel(inputfile, index_col = 'Id')
data_zs = 1.0*(data - data.mean()) / data.std() #数据标准化
from sklearn.cluster import KMeans
model = KMeans(n_clusters=k, n_jobs=4, max_iter=iteration)
model.fit(data_zs) #开始聚类
#简单打印结果
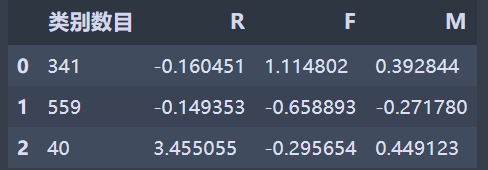
r1 = pd.Series(model.labels_).value_counts() #统计各个类别的数目
r2 = pd.DataFrame(model.cluster_centers_) #找出聚类中心
r = pd.concat([r1, r2], axis=1) #横向连接
r.columns = [u'类别数目'] + list(data.columns) #表头重命名
r
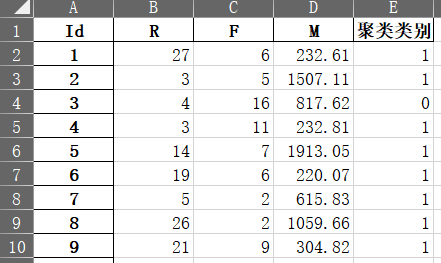
#详细输出原始数据及其类别
r = pd.concat([data, pd.Series(model.labels_, index=data.index)], axis=1)
r.columns = list(data.columns) + [u'聚类类别'] #表头重命名
r.to_excel(outputfile)
接着绘制不同客户分群的概率密度函数图,通过这些图能直观地比较不同客户群的价值,代码如下:
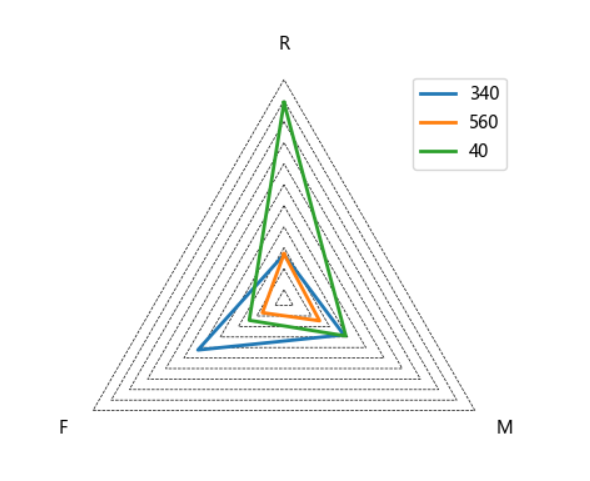
绘制聚类后的概率密度图:
#画概率密度图
def density_plot(data):
import matplotlib.pyplot as plt
#中文和负号的正常显示
plt.rcParams['font.sans-serif'] = 'Microsoft YaHei'
plt.rcParams['axes.unicode_minus'] = False
p = data.plot(kind='kde',linewidth=2, subplots=True, sharex=False)
[p[i].set_ylabel(u'密度') for i in range(k)]
plt.legend()
return plt
pic_output = 'G:/Python数据分析与挖掘实战/chapter5/zl/pd_'
for i in range(k):
density_plot(data[r[u'聚类类别']==i]).savefig(u'%s%s.png' % (pic_output, i))
分群1的概率密度函数图:
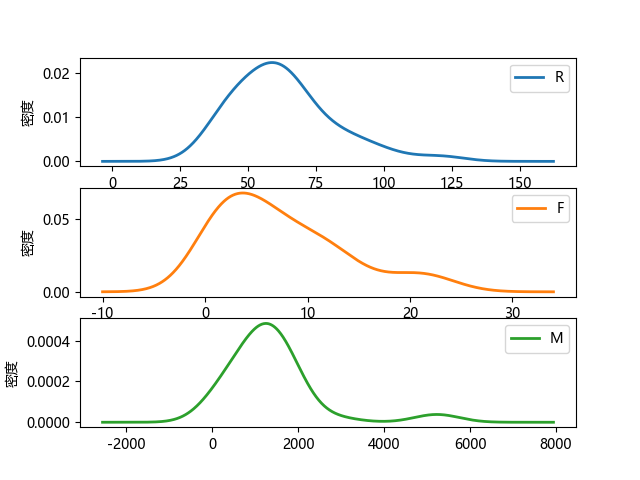
特点:
- R间隔相对较大,间隔分布在30-80天;
- 消费次数集中在0-15次;
- 消费金额在0-2000;
分群2的概率密度函数图:
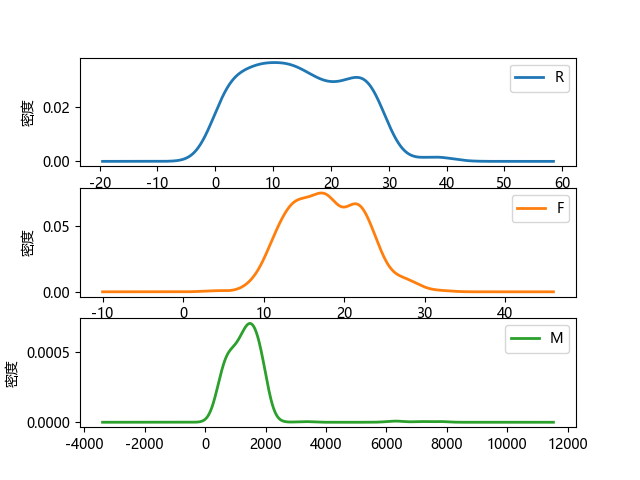
特点:
- R间隔相对较小,主要集中在0-30天;
- 消费次数集中在10-25次;
- 消费金额在500-2000;
分群3的概率密度函数图:
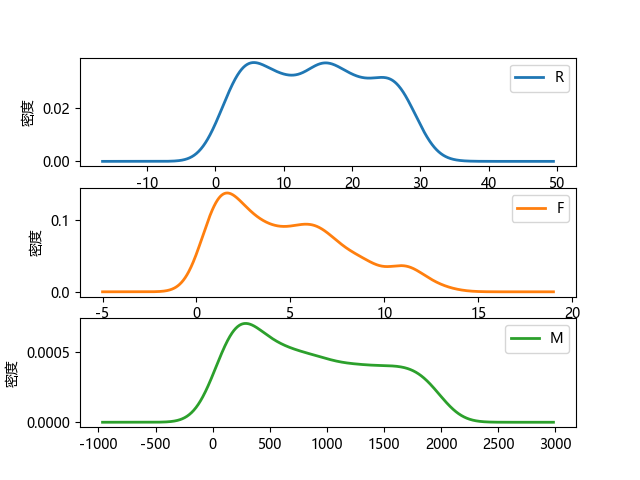
特点:
- R间隔分布在0-30天;
- 消费次数集中在0-12次;
- 消费金额在0-1800;
对比分析:
- 分群1时间间隔较长,消费次数较小,消费金额也不是特别高,是价值较低的客户群体
- 分群2时间间隔较短,消费次数多,而且消费金额较大,是高消费、高价值客户群体
- 分群3的时间间隔、消费次数和消费金额都处于中等水平,代表着一般客户群体
5.2.2 聚类分析算法评价
聚类分析仅根据样本数据本身将样本分组。其目标是实现组内的对象相互之间是相似的(相关的),而不同组中的对象是不同的(不相关的)。组内的相似性越大,组间差别越大,聚类效果就越好。
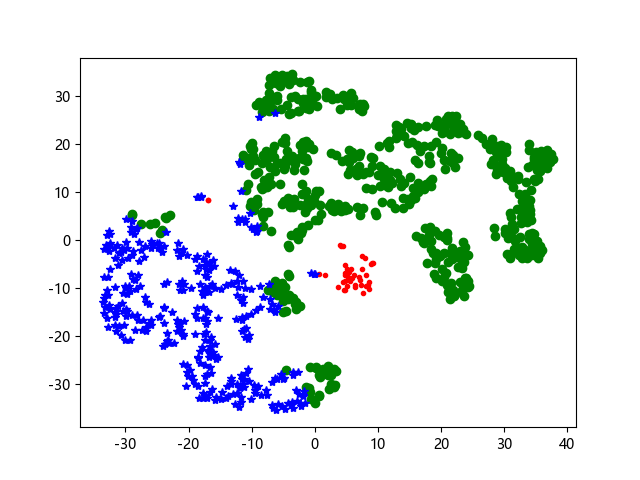
5.2.3 聚类结果可视化—TSNE
#TSNE进行数据降维并展示聚类结果
from sklearn.manifold import TSNE
tsne = TSNE()
tsne.fit_transform(data_zs) #进行数据降维
tsne = pd.DataFrame(tsne.embedding_, index=data_zs.index) #转换数据格式,embedding_嵌入向量
import matplotlib.pyplot as plt
#中文和负号的正常显示
plt.rcParams['font.sans-serif'] = 'Microsoft YaHei'
plt.rcParams['axes.unicode_minus'] = False
#不同类别用不同颜色和样式绘图
d = tsne[r[u'聚类类别'] == 0]
plt.plot(d[0], d[1], 'r.')
d = tsne[r[u'聚类类别'] == 1]
plt.plot(d[0], d[1], 'go')
d = tsne[r[u'聚类类别'] == 2]
plt.plot(d[0], d[1], 'b*')
plt.show()
5.3 关联规则
关联规则目的是在一个数据集中找出各项之间的关联关系,而这种关系并没有在数据中直接表示出来。
5.3.1 常用关联规则算法
- Apriori
- FP-Tree
- Eclat算法
- 灰色关联法
5.3.2 Apriori算法
第一次实现了在大数据集上可行的关联规则提取,核心思想是通过连接产生候选项与其支持度,然后通过剪枝生成频繁项集。
1.关联规则和频繁项集
(1)关联规则的一般形式:
- 项集A、B同时发生的概率:支持度(相对支持度)
S u p p o r t ( A ⇒ B ) = P ( A ∪ B ) = A 、 B 同 时 发 生 的 事 务 个 数 所 有 事 务 个 数 Support(ARightarrow B)=P(Acup B)=frac{A、B同时发生的事务个数}{所有事务个数} Support(A⇒B)=P(A∪B)=所有事务个数A、B同时发生的事务个数
- 若项集A发生,则项集B发生的概率:置信度
C o n f i d e n c e ( A ⇒ B ) = P ( B ∣ A ) = A 、 B 同 时 发 生 的 事 务 个 数 A 发 生 的 事 务 个 数 Confidence(ARightarrow B)=P(B|A)=frac{A、B同时发生的事务个数}{A发生的事务个数} Confidence(A⇒B)=P(B∣A)=A发生的事务个数A、B同时发生的事务个数
(2)最小支持度和最小置信度:
- 最小支持度是用户或专家定义的衡量支持度的一个阈值,表示项目集在统计意义上的最低重要性
- 最小置信度是用户或专家定义的衡量置信度的一个阈值,表示关联规则的最低可靠性
同时满足最小支持度阈值和最小置信度阈值的规则称作强规则。
(3)项集
项集是项的集合,包含k个项的项集称为k项集。项集的出现频率是所有包含项集的事务计数,又称作绝对支持度或支持度计数。如果项集I的相对支持度满足预定义的最小支持度阈值,则I是频繁项集。
(4)支持度计数
项集A的支持度计数是事务数据集中包含项集A的事务个数,简称为项集的频率或计数。
Apriori算法的函数代码:
#Apriori算法
#相关函数参考代码apriori.py
from __future__ import print_function
import pandas as pd
inputfile = 'G:/Python数据分析与挖掘实战/chapter5/demo/data/menu_orders.xls'
outputfile = 'G:/Python数据分析与挖掘实战/chapter5/zl/apriori_rules.xlsx'
data = pd.read_excel(inputfile, header=None)
print(u'n转换原始数据至0-1矩阵...')
ct = lambda x: pd.Series(1, index=x[pd.notnull(x)]) #转换0-1矩阵的过渡函数
b = map(ct, data.values) #map方式执行
data = pd.DataFrame(list(b)).fillna(0) #实现矩阵转换,空值用0填充
print('转完毕。')
del b #删除中间变量b,节省内存
support = 0.2 #最小支持度
confidence = 0.5 #最小置信度
ms = '---' #连接符,默认’--‘
find_rule(data, support, confidence, ms).to_excel(outputfile)
结果为:
support confidence
e---a 0.3 1.000000
e---c 0.3 1.000000
c---e---a 0.3 1.000000
a---e---c 0.3 1.000000
c---a 0.5 0.714286
a---c 0.5 0.714286
a---b 0.5 0.714286
c---b 0.5 0.714286
b---a 0.5 0.625000
b---c 0.5 0.625000
a---c---e 0.3 0.600000
b---c---a 0.3 0.600000
a---c---b 0.3 0.600000
a---b---c 0.3 0.600000
其中:
- e- - - a表示e发生能够推出a发生,置信度为100%,支持度为30%
- b- - - c - - - a表示b、c同时发生能够推出a发生,置信度为60%,支持度为30%
搜索出来的关联规则不一定具有实际意义,需要根据问题背景筛选适当的有意义的规则,并赋予合理的解释。
2. Apriori算法:使用筛选产生频繁项集
Apriori算法的主要思想是:
- 找出存在于事务数据集中的最大的频繁项集;
- 在利用得到的最大频繁项集与预先设定的最小置信度阈值生成强关联规则;
(1)Apriori的性质:频繁项集的所有非空子集也必须是频繁项集
(2)Apriori算法实现的两个过程:
- 找出所有的频繁项集(支持度必须大于等于给定的最小支持度阈值),在这个过程中连接步和剪枝步相互融合,最终得到最大频繁项集 L k L_{k} Lk。
- 由频繁项集产生强关联规则:满足预定的最小置信度阈值
餐饮行业的实例:
从中抽取10个点餐订单作为事务数据集,设支持度为0.2,为方便起见将菜品分别简记为{a, b, c, d, e}。


过程一:找最大k项频繁集
- 扫描所有事务,计算每一项的支持度。例如,P({a}) = 7/10 = 0.7
- 与最小支持度阈值进行比较,保留大于或等于该阈值的项,得1项频繁集 L 1 L_{1} L1
- 扫描所有事务,连接得到2项集 C 2 C_{2} C2,并计算每一项的支持度。例如,P({a,b}) = {a,b} / 所有事务个数 = 5/10 = 0.5
- 接着进行剪枝步,剔除非频繁集,保留大于或等于最小支持度阈值,得2项频繁集 L 2 L_{2} L2
- 扫描所有事务,由 L 1 L_{1} L1和 L 2 L_{2} L2连接得候选3项集 C 3 C_{3} C3,并计算每一项的支持度。例如,P({a, b, c}) = {a, b, c} / 所有事务个数 = 3/10 = 0.3
- 接着进行剪枝步,剔除非频繁集,保留大于或等于最小支持度阈值,得2项频繁集 L 3 L_{3} L3
- L 3 L_{3} L3与 L 1 L_{1} L1连接得到候选4项集 C 4 C_{4} C4,易得剪枝后为空集,最后得到最大3项频繁集{a, b, c}和{a, c, e}
过程二:由频繁集产生关联规则
筛选出大于或等于最小置信度的频繁集即为强关联规则
例如,a>b, 50%, 71.7286%表示:客户同时点菜品a和b的概率是50%,点了菜品a,再点菜品b的概率是71.4286%。知道了这些,就可以对顾客进行智能推荐,增加销量同时满足客户需求。
最后
以上就是小巧小鸭子最近收集整理的关于python数据分析与挖掘实战—第5章(挖掘建模)(2)分类与预测算法评价5.2 聚类分析5.3 关联规则的全部内容,更多相关python数据分析与挖掘实战—第5章(挖掘建模)(2)分类与预测算法评价5.2内容请搜索靠谱客的其他文章。








发表评论 取消回复