-
真值:真值可以理解为一个值本身真正的值
-
机器码:一个值在计算机中的二进制表示形式,具体有原码 [ x ] 原 [x]_原 [x]原、反码 [ x ] 反 [x]_反 [x]反、补码 [ x ] 补 [x]_补 [x]补、移码 [ x ] 移 [x]_移 [x]移 这些形式
进制表示
一般书写可以在数值右下方注上基数 n 表示 n 进制
????例子
( 3235119104 ) 10 = ( 11000000110101000000000000000000 ) 2 = ( C 0 D 40000 ) 16 {(3235119104)}_{10}={(1100 0000 1101 0100 0000 0000 0000 0000)}_{2}={(C0D40000)}_{16} (3235119104)10=(11000000110101000000000000000000)2=(C0D40000)16
一般书写也可以在数值末尾增添后缀表示该数值的进制
- B:二进制(binary)
- H:十六进制(hexadecimal)
- D:十进制(decimal)
- O:八进制(octal)
????例子
( 3235119104 ) D = ( 11000000110101000000000000000000 ) B = ( C 0 D 40000 ) H {(3235119104)}D={(1100 0000 1101 0100 0000 0000 0000 0000)}B={(C0D40000)}H (3235119104)D=(11000000110101000000000000000000)B=(C0D40000)H
在C语言中,通过添加前缀表示数值的进制
- 0b 或 0B:二进制(binary)
- 0x 或 0X:十六进制(hexadecimal)
- 0:八进制(octal)
????例子
3235119104 = 0 b 11000000110101000000000000000000 = 0 x C 0 D 40000 3235119104=0b1100 0000 1101 0100 0000 0000 0000 0000=0xC0D40000 3235119104=0b11000000110101000000000000000000=0xC0D40000
进制转换
十进制整数转换为二进制整数
"除 2 取余,逆序排列"法
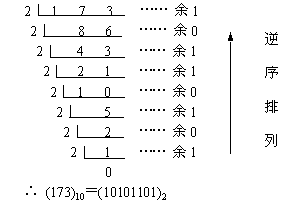
十进制小数转换为二进制小数
"乘 2 取整,顺序排列"法

定点数表示
无符号数
通常只有无符号整数,没有无符号小数
????注释
如 C 语言就没有
unsigned float,unsigned double
n n n 位无符号数表示范围为 [ 0 , 2 n − 1 ] [0,2^n-1] [0,2n−1]
有符号数的定点表示
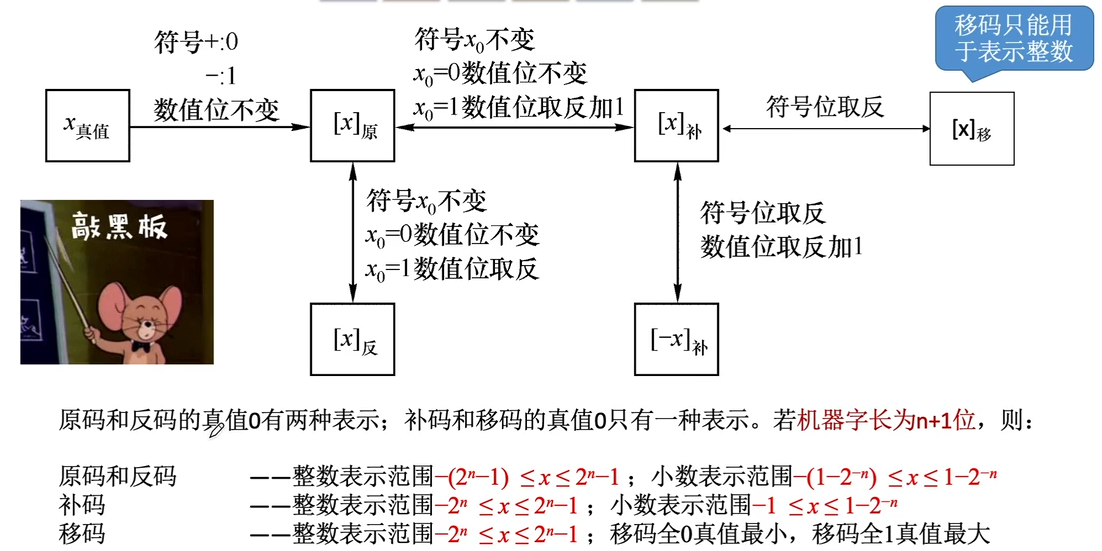
真值 x x x 可以用原码 [ x ] 原 [x]_原 [x]原、反码 [ x ] 反 [x]_反 [x]反、补码 [ x ] 补 [x]_补 [x]补 表示其对应的定点整数和定点小数
还可用移码 [ x ] 移 [x]_移 [x]移 表示定点整数
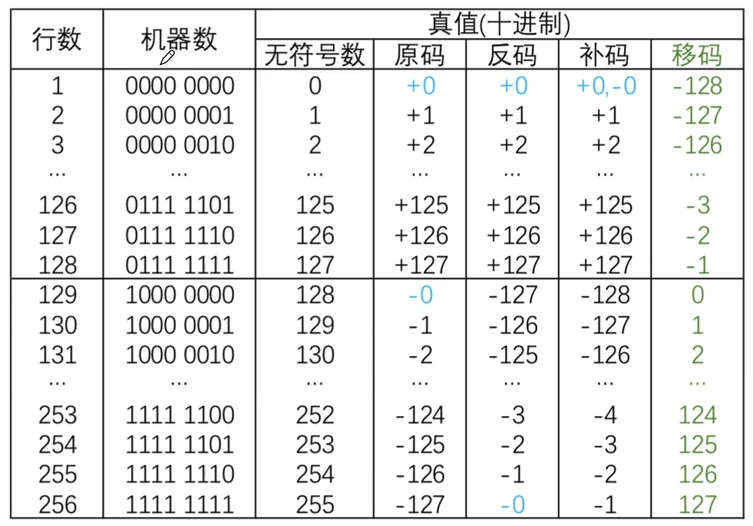
原码
原码由符号位和数值位(尾数)构成
- 符号位用”0/1“对应”正/负“
- 尾数表示真值的二进制绝对值
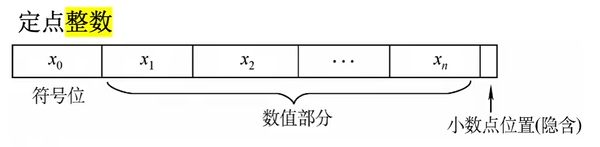
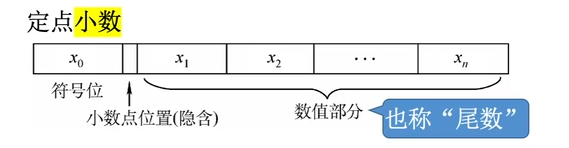
- n + 1 n+1 n+1 位整数原码表示范围为 [ − ( 2 n − 1 ) , 2 n − 1 ] [-(2^n-1),2^n-1] [−(2n−1),2n−1]
- 真值 0 有 +0 和 -0 两种形式( [ + 0 ] 原 = 00000000 , [ − 0 ] 原 = 10000000 [+0]_原=00000000,[-0]_原=10000000 [+0]原=00000000,[−0]原=10000000)
反码
- 正数的反码就是原码
- 负数的反码则是在原码的基础上,符号位不动,数值位全部取反

- n+1 位整数反码表示范围为 [ − ( 2 n − 1 ) , 2 n − 1 ] [-(2^n-1),2^n-1] [−(2n−1),2n−1]
- 真值 0 有 +0 和 -0 两种形式( [ + 0 ] 原 = 01111111 , [ − 0 ] 原 = 11111111 [+0]_原=01111111,[-0]_原=11111111 [+0]原=01111111,[−0]原=11111111)
补码
- 正数的补码就是原码
- 负数的补码为反码 +1

- n+1 位整数补码表示范围为 [ − 2 n , 2 n − 1 ] [-2^n,2^n-1] [−2n,2n−1]
- 真值 0 的 +0 和 -0 都是一种形式( [ + 0 ] 补 = [ − 0 ] 补 = 00000000 [+0]_补=[-0]_补=00000000 [+0]补=[−0]补=00000000)
- 规定定点整数补码 [ x ] 补 = 10000000 [x]_补=10000000 [x]补=10000000 表示 x x x 真值为 2 − 7 2^{-7} 2−7
- 规定定点小数补码 [ x ] 补 = 1.0000000 [x]_补=1.0000000 [x]补=1.0000000 表示 x x x 真值为 − 1 -1 −1
移码
补码的基础上将符号位取反
只能用于表示整数
计算定点小数真值的技巧
如补码 1.1001 对应真值 − 0.0111 B = − ( 2 − 2 D + 2 − 3 D + 2 − 4 D ) -0.0111B=-(2^{-2}D+2^{-3}D+2^{-4}D) −0.0111B=−(2−2D+2−3D+2−4D)
但也可以理解为 -111B 右移 4 位,即 − 111 B = 7 2 4 D = 7 16 D -111B=frac{7}{2^4}D=frac{7}{16}D −111B=247D=167D
运算
移位
逻辑左移:整体左移,右边补 0
逻辑右移:整体右移,左边补 0
算术左移:整体左移,右边补 0
算数右移:整体右移,左边补和符号位一样的值
- 算术左移和算术右移主要用来进行有符号数的倍增、减半
- 逻辑左移和逻辑右移主要用来进行无符号数的倍增、减半
[ A + B ] 补 = [ A ] 补 + [ B ] 补 [ A − B ] 补 = [ A ] 补 + [ − B ] 补 [ − B ] 补 : [ B ] 补 连同符号位一起取反 + 1 {[A+B]}_{补}={[A]}_{补}+{[B]}_{补}\ {[A-B]}_{补}={[A]}_{补}+{[-B]}_{补}\ {[-B]}_{补}:{[B]}_{补}连同符号位一起取反+1 [A+B]补=[A]补+[B]补[A−B]补=[A]补+[−B]补[−B]补:[B]补连同符号位一起取反+1
判断溢出
双符号位补码:模 4 补码
单符号位补码:模 2 补码
单符号位判断
V = A S B s S S ‾ + A S ‾ B S ‾ S S V=A_SB_soverline{S_S}+overline{A_S}overline{B_S}S_S V=ASBsSS+ASBSSS
A 符号位 A S A_S AS,B 符号位 B S B_S BS,运算结果为 S S S_S SS
V=0 表示无溢出
V=1 表示有溢出
双符号位判断
正数补码符号位负数补码符号位是 11
01 是上溢,10 是下溢
补码一位乘法


浮点数表示
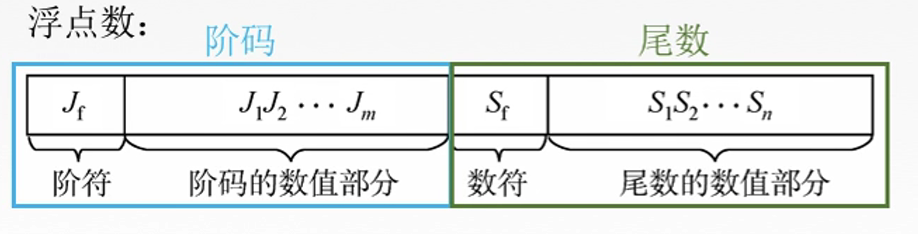
浮点数由阶码 E(Exponent)和尾数 M(Mantissa)构成
阶码 E 是定点整数,尾数 M 是定点小数,相当于用两个定点数表示一个浮点数
- 阶码 E 反应浮点数表示范围以及小数点实际位置
- 尾数 M 的数值部分的位数反映浮点数的精度
浮点数的真值 N = M × r E N=M×r^E N=M×rE,r 是阶码的底,一般为 2
- 阶码通常用移码或补码表示
- 尾数通常用原码或补码表示


浮点数的规格化
规定尾数最高数位必须是一个有效值
规格化的尾数十进制真值的范围为 0.25 ≤ M ≤ 1 0.25leq Mleq 1 0.25≤M≤1



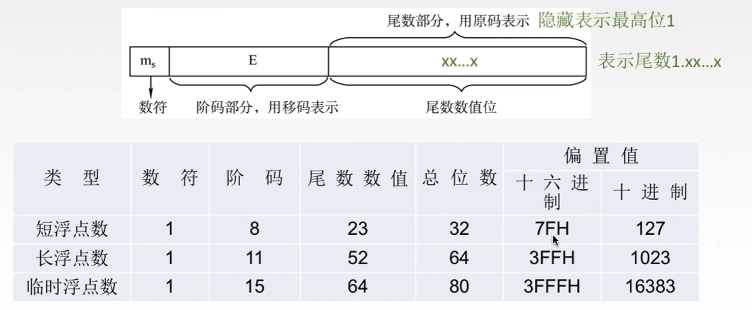
IEEE754 标准
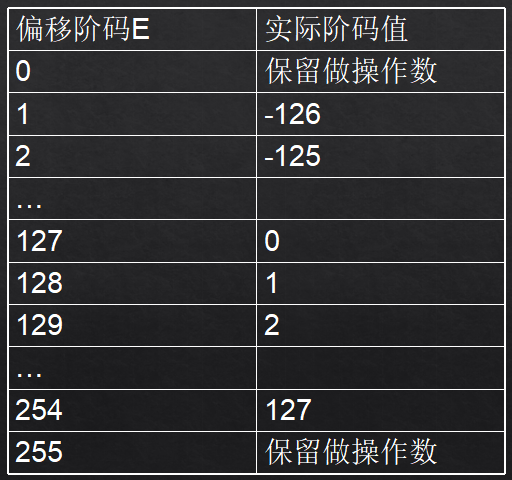
数据类型及存储规定

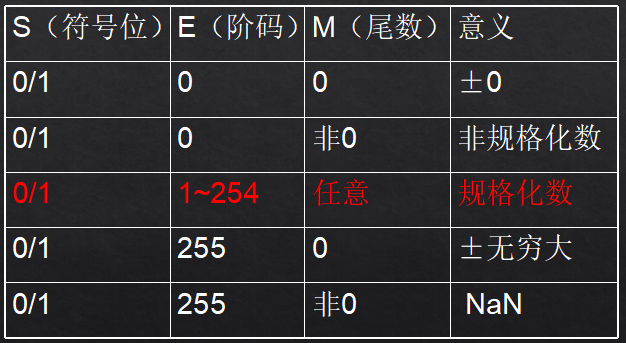
- +0:所有的数据位都是 0
- -0:最高位为1,其它的数据位是 0
- 正/负无穷大::符号位为 0/1,阶码位全为 1,有效数字全为 0
- NaN(Not A Number)::非法的浮点数,阶码位全为 1,有效数字不全为 0
特殊数据的相关计算规定
- 无穷大+任何数=无穷大
- 任何有限数÷0=无穷大
- 任何有限数÷无穷大=0
- 无穷大÷无穷大=NaN
最值

C语言变量类型
C语言中没有定点小数相关的变量类型
以下是不同变量类型在不同位机下所占的大小(单位为字节)
| 32位机 | 64位机 | |
|---|---|---|
| 字符型 char | 1 | 1 |
| 短整型 short | 2 | 2 |
| 整型 int | 4 | 4 |
| 长整型 long | 4 | 8(4?) |
| 长长整型 long long | 8 | 8 |
| 单精度浮点型 float | 4 | 4 |
| 双精度浮点型 double | 8 | 8 |
可通过在数值末尾添加后缀表示该数值的变量类型,对应关系如下

最后
以上就是包容外套最近收集整理的关于计算机中数据信息的表示的全部内容,更多相关计算机中数据信息内容请搜索靠谱客的其他文章。








发表评论 取消回复