Median on Segments (Permutations Edition)

+传送门+

◇题意◇

给定一个长度为$n$的序列，问在它的子序列中，有多少个满足该序列的中位数为$m$；

注意：若序列长度为偶数则中位数为中间偏左
例如：在1 2 3 4 中的中位数为2

◇解析◇

中位数的性质

定义比中位数大的数为$A$，比中位数小的数为$B$
在序列中$Num_A=Num_B$
在题目定义中还可以是$Num_A=Num_B+1$

基本想法

$Num_Al-Num_Bl=Num_Br-Num_Ar$
即该段区间中
$Num_Al+Num_Ar=Num_Bl+Num_Br$
同上
$Num_A=Num_B$

再进一步

如何实现呢？
一个显然的想法，分别记录某一段区间内的
$Num_A$与$Num_B$；
自然，我们想到用前缀和记录
$Num_Ai$与$Num_Bi$；
但事实上我们需要记录的只有
$deltai（Num_Ai-Num_Bi）$；

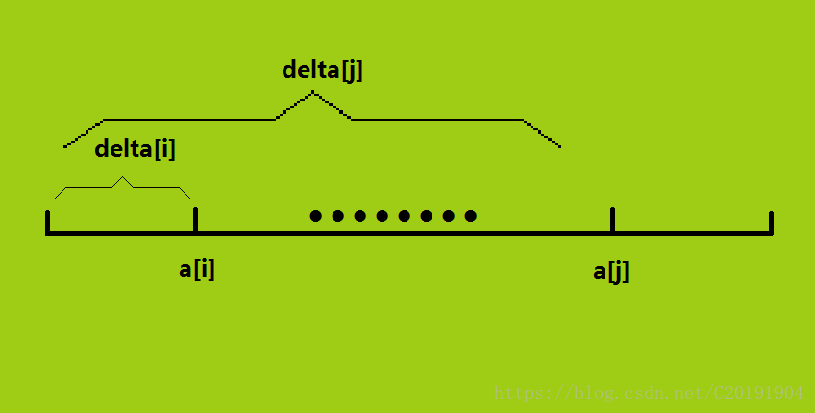
其中$delta[i]=A[i]-B[i]$，$delta[j]=A[j]-B[j]$
在序列$a[i...j]$中，若满足：
$\ $ $A[j]-A[i]=B[j]-B[i]$(即$Num_A[i...j]$==$Num_B[i...j]$)
——> $delta[j]-delta[i]=0$
——> $delta[j]=delta[i]$
则序列$a[i...j]$为一满足$m$为中位数的序列。

注意：
(1)$A[]$,$B[]$,$delta[]$都为前缀和
(2)$a[i]$,$a[j]$分别在$m$两侧

别把这个忘了

上图“注意”中：显然在此序列中不满足$delta[j]=delta[i]$；
那我们再推一遍
$\ $ $A[j]-A[i]=B[j]-B[i]+1$(即$Num_A[i...j]$==$Num_B[i...j]+1$)
——> $delta[j]-delta[i]=1$
——> $delta[j]-1=delta[i]$

◇算法实现◇

显然，在上文思路中有几个关键的变量
$delta[]$,现在扫描到m的哪一侧（$delta[i]$与$delta[j]$分别在m两侧），m两侧分别可以配对的区间数即$delta$相等的点数；

变量定义

因此，我们定义如下几个变量
（1）$int$ $delta$
（为何不是数组？在求解过程中，我们需要统计的是$m$两侧分别可以配对的区间数，及某两节点$delta$相等的数量，则我们只需记录m左侧值为$delta$的点数，再在$m$右侧用某时$delta$配对即可）
（2）$bool$ $flag$
（现在扫描过m吗，即此刻是在m的左侧否）
（为何要记录？在（1）中已经解释了，m左边是统计，右边是配对）
（3）$cnt[]$
（下标为$delta$，记录delta为某一值的点数，方便在m右侧配对时统计数量）

算法流程

（1）在输入过程中维护$delta$和$flag$(输入=$m$，)
①$flag=0$→$cnt[delta]++$
②$flag=1$→$ans+=cnt[delta]+cnt[delta-1]$
（$cnt[delta-1]$即$delta[j]-1=delta[i]$型的配对）
（2）很容易想到，$delta$极有可能在某一时刻为一负数，因此，我们将$cnt$的坐标向右平移$MAXN$位，轻松的解决了这个简单的问题。

◇代码◇

/*Wiz*/
#include<cstdio>
#include<map>
#include<algorithm>
using namespace std;
typedef long long LL;
const int MAXN=2*int(1e5);
int del;
int n,m;
int C[2*MAXN+5];
int main()
{
    int x;
    LL ans=0;
    bool f=0;
    C[MAXN]=1;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) {
        scanf("%d",&x);
        if(x>m) del++;
        if(x<m) del--;
        if(x==m) f=1;
        if(f)
            ans+=C[del+MAXN]+C[del-1+MAXN];
        else C[del+MAXN]++;
    }
    printf("%lld",ans);
}

再说两句

这道题建议使用读入优化；
不是说不用很慢，过不了，但用了效率速度就很快了。

$Thanks$ $For$ $Reading!$

最后

以上就是文静小丸子为你收集整理的CodeForces - 1005E1 Median on Segments (Permutations Edition)Median on Segments (Permutations Edition)的全部内容，希望文章能够帮你解决CodeForces - 1005E1 Median on Segments (Permutations Edition)Median on Segments (Permutations Edition)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。