[HNOI2018]毒瘤

Description
从前有一名毒瘤。

毒瘤最近发现了量产毒瘤题的奥秘。考虑如下类型的数据结构题：给出一个数组，要求支持若干种奇奇怪怪的修改操作（比如区间加一个数，或者区间开平方），并支持询问区间和。毒瘤考虑了(n)个这样的修改操作，并编号为(1sim n)。当毒瘤要出数据结构题的时候，他就将这些修改操作中选若干个出来，然后出成一道题。

当然了，这样出的题有可能不可做。通过精妙的数学推理，毒瘤揭露了这些修改操作的关系：有(m)对“互相排斥”的修改操作，第(i)对是第(u_i)个操作和第(v_i)个操作。当一道题同时含有(u_i)和(v_i)这两个操作时，这道题就会变得不可做。另一方面，一道题中不包含任何“互相排斥”的修改操作时，这个题就是可做的。此外，毒瘤还发现了一个规律：(m-n)是一个很小的数字，且任意两个修改操作都是连通的。两个修改操作(a,b)是连通的，当且仅当存在若干操作(t_0,t_1,...,t_l)，使得(t_0=a,t_l=b)，且对(1leqslant ileqslant l)，(t_{i-1})和(t_i)都是“互相排斥”的修改操作。

一堆“互相排斥”的修改操作称为互斥对。现在毒瘤想知道，给定值(n)和(m)个互斥对，他共能出出多少道可做的不同的数据结构题。两道数据结构题是不同的，当且仅当有一个修改操作在其中一道题中存在，而在另一道题中不存在。

Input
第一行为正整数(n,m)。
接下来(m)行，每行两个正整数(u,v)，代表一对“互相排斥”的修改操作。

Output
输出一行一个整数，代表毒瘤可以出的可做的不同的“互相排斥”的修改操作的个数。这个数可能很大，所以只输出模998244353后的值。

Sample Input 1
3 2
1 2
2 3

Sample Output 1
5

Sample Input 2
6 8
1 2
1 3
1 4
2 4
3 5
4 5
4 6
1 6

Sample Output 2
16

Sample Input 3
12 18
12 6
3 11
8 6
2 9
10 4
1 8
6 2
11 5
10 6
12 2
9 3
7 6
2 7
3 2
7 3
5 6
2 11
12 1

Sample Output 3
248

HINT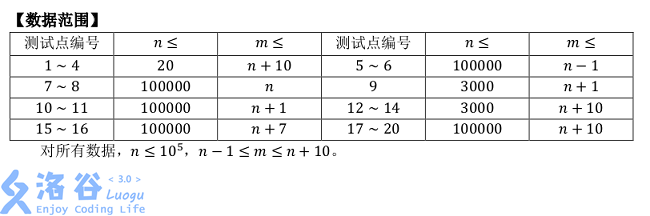

---

首先考虑(m=n-1)的情况，我们直接做一遍tree dp，设(f[u][0/1])表示点(u)选或不选的方案数，转移即为[begin{cases}f[u][0]=prodlimits_{urightarrow v}(f[v][0]+f[v][1])\f[u][1]=prodlimits_{urightarrow v}f[v][0]end{cases}]

这样我们可以得到10pts的好成绩，那么多出来的非树边如何处理？因为最多只有11条非树边，暴力枚举端点状态，只有((1,0),(0,0),(0,1))三种，但其实只要枚举一个点选或不选，((0,0))和((0,1))可以合并起来，复杂度(O(2^{m-n+1}n))，可以得到75pts的好成绩

如何拿满分？我们发现上面的算法重复计算了很多状态，我们把非树边影响的点取出来，记为关键点，影响dp值的只有这些点，我们把这些关键点（至多22个）建立一棵虚树，dp方程可以转化为[begin{cases}f[u][0]=prodlimits_{urightarrow v}k_{urightarrow v,0,0}times f[v][0]+k_{urightarrow v,0,1}times f[v][1]\f[u][1]=prodlimits_{urightarrow v}k_{urightarrow v,1,0}times f[v][0]+k_{urightarrow v,1,1}times f[v][1]end{cases}]

其实可以发现，(k_{urightarrow v,0/1,0/1})是不会变化的，那么我们就先预处理出系数，如何求？(v)在原树上暴力向上跳，累计统计系数即可，记得统计的时候不能重复统计

这样转移的复杂度是(O(n))的，对于虚树上的边我们暴力枚举状态，然后转移，记(s)为关键点数，则复杂度为(O(n+s2^s))

/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define Fi first
#define Se second
#define MK make_pair
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef pair<int,int> pii;
typedef unsigned long long ull;
inline char gc(){
    static char buf[1000000],*p1=buf,*p2=buf;
    return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
inline int frd(){
    int x=0,f=1; char ch=gc();
    for (;ch<'0'||ch>'9';ch=gc())   if (ch=='-')    f=-1;
    for (;ch>='0'&&ch<='9';ch=gc()) x=(x<<3)+(x<<1)+ch-'0';
    return x*f;
}
inline int read(){
    int x=0,f=1; char ch=getchar();
    for (;ch<'0'||ch>'9';ch=getchar())  if (ch=='-')    f=-1;
    for (;ch>='0'&&ch<='9';ch=getchar())    x=(x<<3)+(x<<1)+ch-'0';
    return x*f;
}
inline void print(int x){
    if (x<0)    putchar('-'),x=-x;
    if (x>9)    print(x/10);
    putchar(x%10+'0');
}
const int N=1e5,Mod=998244353;
struct S1{
    int x,y;
    S1(){x=y=0;}
    void insert(int _x,int _y){x=_x,y=_y;}
}NT[15];//Not in Tree
int NT_cnt,dfn[N+10];
bool cmp(int x,int y){return dfn[x]<dfn[y];}
struct S2{
    int pre[(N<<1)+10],now[N+10],child[(N<<1)+10],tot,Time;
    int fa[N+10],size[N+10],deep[N+10],Rem[N+10],top[N+10],f[N+10][2];
    bool vis[N+10];
    void join(int x,int y){pre[++tot]=now[x],now[x]=tot,child[tot]=y;}
    void insert(int x,int y){join(x,y),join(y,x);}
    void dfs(int x){
        deep[x]=deep[fa[x]]+1,size[x]=1;
        for (int p=now[x],son=child[p];p;p=pre[p],son=child[p]){
            if (son==fa[x]) continue;
            fa[son]=x,dfs(son);
            size[x]+=size[son];
            if (size[Rem[x]]<size[son]) Rem[x]=son;
        }
    }
    void build(int x){
        if (!x) return;
        dfn[x]=++Time;
        top[x]=Rem[fa[x]]==x?top[fa[x]]:x;
        build(Rem[x]);
        for (int p=now[x],son=child[p];p;p=pre[p],son=child[p]){
            if (son==fa[x]||son==Rem[x])    continue;
            build(son);
        }
    }
    int LCA(int x,int y){
        while (top[x]!=top[y]){
            if (deep[top[x]]<deep[top[y]])  swap(x,y);
            x=fa[top[x]];
        }
        return deep[x]<deep[y]?x:y;
    }
    void dp(int x){//在原树上dp一次，处理出原本的dp系数f
        f[x][0]=f[x][1]=1;
        for (int p=now[x],son=child[p];p;p=pre[p],son=child[p]){
            if (son==fa[x]) continue;
            dp(son);
            f[x][1]=1ll*f[x][1]*f[son][0]%Mod;
            f[x][0]=1ll*f[x][0]*(f[son][0]+f[son][1])%Mod;
        }
    }
    int work(int x,int y,int xv,int yv){//deep[x]<deep[y]
        //暴力上跳，求出边的系数
        static int tmp[2];
        tmp[yv]=1,tmp[yv^1]=0;
        while (x!=y){
            vis[y]=1;
            for (int p=now[y],son=child[p];p;p=pre[p],son=child[p]){
                if (son==fa[y]||vis[son])   continue;
                tmp[1]=1ll*tmp[1]*f[son][0]%Mod;
                tmp[0]=1ll*tmp[0]*(f[son][0]+f[son][1])%Mod;
            }
            swap(tmp[0],tmp[1]);
            tmp[0]=(tmp[0]+tmp[1])%Mod;
            //f[x][1]=f[son][0];
            //f[x][0]=f[son][0]+f[son][1];
            //向上跳一次要按如上方法转移，所以tmp数组需要按如上方法处理
            y=fa[y];
        }
        return tmp[xv];
    }
    pii work(int x){//处理关键点在虚树上应有的值
        static int tmp[2];
        tmp[0]=tmp[1]=1;
        for (int p=now[x],son=child[p];p;p=pre[p],son=child[p]){
            if (son==fa[x]||vis[son])   continue;
            vis[son]=1;
            tmp[1]=1ll*tmp[1]*f[son][0]%Mod;
            tmp[0]=1ll*tmp[0]*(f[son][0]+f[son][1])%Mod;
        }
        return MK(tmp[0],tmp[1]);
    }
}HLD;//Heavy Light Decomposition
const int M=22;
struct S3{
    int pre[(M<<2)+10],now[N+10],child[(M<<2)+10],tot,m;
    int V[(M<<2)+10][2][2];//V[p][i][j]: p:u->v i:u(0/1) j:v(0/1)
    int vis[N+10];//special point(0/1); normal point(-1)
    int f[N+10][2],g[N+10][2],A[M+10];
    void join(int x,int y){pre[++tot]=now[x],now[x]=tot,child[tot]=y;}
    void insert(int x,int y){join(x,y),join(y,x);}
    void rebuild(){
        static int stack[(M<<1)+10],top=0;
        for (int i=1;i<=NT_cnt;i++) A[++m]=NT[i].x,A[++m]=NT[i].y;
        sort(A+1,A+1+m);
        m=unique(A+1,A+1+m)-A-1;
        stack[++top]=1;
        sort(A+1,A+1+m,cmp);
        for (int i=1;i<=m;i++){
            int x=A[i],lca=HLD.LCA(x,stack[top]);
            if (x==1)   continue;
            if (lca==stack[top]){
                stack[++top]=x;
                continue;
            }
            while (true){
                int y=stack[top-1];
                if (dfn[y]>=dfn[lca])   insert(stack[top--],y);
                else{
                    if (lca==stack[top])    break;
                    insert(stack[top],lca);
                    stack[top]=lca; break;
                }
            }
            stack[++top]=x;
        }
        while (top>1){
            insert(stack[top-1],stack[top]);
            top--;
        }
    }
    void prepare(int x,int fa){
        for (int p=now[x],son=child[p];p;p=pre[p],son=child[p]){
            if (son==fa)    continue;
            prepare(son,x);
            for (int i=0;i<2;i++)
                for (int j=0;j<2;j++)
                    V[p][i][j]=HLD.work(x,son,i,j);
        }
        //求出每个点本身应有的dp值，边的系数只考虑边，不考虑端点
        pii tmp=HLD.work(x);
        g[x][0]=tmp.Fi,g[x][1]=tmp.Se;
    }
    void dp(int x,int fa){
        if (vis[x]==-1) f[x][0]=g[x][0],f[x][1]=g[x][1];
        else    f[x][vis[x]]=g[x][vis[x]],f[x][vis[x]^1]=0;
        for (int p=now[x],son=child[p];p;p=pre[p],son=child[p]){
            if (son==fa)    continue;
            dp(son,x);
            f[x][1]=1ll*f[x][1]*(1ll*f[son][0]*V[p][1][0]%Mod+1ll*f[son][1]*V[p][1][1]%Mod)%Mod;
            f[x][0]=1ll*f[x][0]*(1ll*f[son][0]*V[p][0][0]%Mod+1ll*f[son][1]*V[p][0][1]%Mod)%Mod;
        }
    }
    void work(){
        rebuild();
        prepare(1,0);
        memset(vis,255,sizeof(vis));
        int Ans=0;
        for (int sta=0;sta<1<<m;sta++){
            for (int i=1;i<=m;i++)  vis[A[i]]=(sta>>(i-1))&1;
            bool flag=1;
            for (int i=1;i<=NT_cnt;i++){
                if (vis[NT[i].x]&&vis[NT[i].y]){
                    flag=0;
                    break;
                }
            }
            if (!flag)  continue;
            dp(1,0);
            Ans=(Ans+(f[1][0]+f[1][1])%Mod)%Mod;
        }
        printf("%dn",Ans);
    }
}VT;//Virtual Tree
struct S4{
    int fa[N+10];
    S4(){for (int i=1;i<=N;i++) fa[i]=i;}
    int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
}DSU;//Disjoint Set Union
int main(){
    int n=read(),m=read();
    for (int i=1;i<=m;i++){
        int x=read(),y=read(),fx,fy;
        if ((fx=DSU.find(x))!=(fy=DSU.find(y))){
            DSU.fa[fx]=fy;
            HLD.insert(x,y);
        }else   NT[++NT_cnt].insert(x,y);
    }
    HLD.dfs(1),HLD.build(1),HLD.dp(1);
    VT.work();
    return 0;
}