dp问题的分析

96 阅读 0 评论 64 点赞

我是靠谱客的博主俊逸大神，最近开发中收集的这篇文章主要介绍dp问题的分析，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

You are given two integers n and m. Calculate the number of pairs of arrays (a,b) such that:

the length of both arrays is equal to m;
each element of each array is an integer between 1 and n (inclusive);
ai≤bi for any index i from 1 to m;
array a is sorted in non-descending order;
array b is sorted in non-ascending order.
As the result can be very large, you should print it modulo 109+7.

Input
The only line contains two integers n and m (1≤n≤1000, 1≤m≤10).

Output
Print one integer – the number of arrays a and b satisfying the conditions described above modulo 109+7.

Examples
Input
2 2
Output
5
Input
10 1
Output
55
Input
723 9
Output
157557417
题意给你两组数一组非降落一组非上升两组数在1，n之间第一组的第几个元素小于第二组数的第几个元素，给你n和这两组数的长度求符合条件的两组数的个数。
刚看到这道题，感觉可以直接dp一次就来结果，后来经过大神指点，恍然大悟。
把第二个翻转后与第一个拼接，就是非降序列，然后一个有1，n之间的数组成的长度一定的非降序列可以这样分解，长度不变，分别由1,2，。。。n结尾的数列的个数相加。
失败代码
若一次搞不出结果就想办法整合。

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
long long f[1001][11];
const int mod=1e9+7;
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=m;i++)
        f[1][i]=1;
    for(int i=1;i<=n;i++)
        f[i][1]=(i*(i+1))/2;
    for(int i=2;i<=n;i++)
        {for(int j=2;j<=m;j++)
    {
        f[i][j]=(f[i-1][j]*2+f[i][j-1])%mod;
    }
        }
    cout<<f[n][m]<<endl;
    return 0;
}

正确代码

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
long long f[1005][25];
const int mm=1e9+7;
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=2*m;i++)
    {
        f[1][i]=1;
    }
    for(int j=1;j<=n;j++)
    {
        f[j][1]=1;
    }
    for(int i=2;i<=n;i++)
    {
        for(int j=2;j<=2*m;j++)
        {
            f[i][j]=(f[i-1][j]+f[i][j-1])%mm;
        }
    }
   /* for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=2*m;j++)
        {
            cout<<f[i][j]<<" ";
        }
        cout<<endl;
    }*/
    long long ans=0;
    int op=2*m;
    for(int i=1;i<=n;i++)
    {
        ans=(ans+f[i][op])%mm;
    }
    cout<<ans<<endl;
    return 0;
}

与之相似的一个问题
Mashmokh’s boss, Bimokh, didn’t like Mashmokh. So he fired him. Mashmokh decided to go to university and participate in ACM instead of finding a new job. He wants to become a member of Bamokh’s team. In order to join he was given some programming tasks and one week to solve them. Mashmokh is not a very experienced programmer. Actually he is not a programmer at all. So he wasn’t able to solve them. That’s why he asked you to help him with these tasks. One of these tasks is the following.

A sequence of l integers b1, b2, …, bl (1 ≤ b1 ≤ b2 ≤ … ≤ bl ≤ n) is called good if each number divides (without a remainder) by the next number in the sequence. More formally for all i (1 ≤ i ≤ l - 1).

Given n and k find the number of good sequences of length k. As the answer can be rather large print it modulo 1000000007 (109 + 7).

Input
The first line of input contains two space-separated integers n, k (1 ≤ n, k ≤ 2000).

Output
Output a single integer — the number of good sequences of length k modulo 1000000007 (109 + 7).

Examples
Input
3 2
Output
5
Input
6 4
Output
39
Input
2 1
Output
2
Note
In the first sample the good sequences are: [1, 1], [2, 2], [3, 3], [1, 2], [1, 3].
f【i】【j】长度为i所用元素为一到 j的个数，
f【i】【j】=f【i-1】【j】+f[i][j的倍数];
最后长度不变，用1，用（1，2），。。。。。。（1，n）的情况加在一起。

#include <iostream>
using namespace std;
const int  pp=1e9+7;
long long f[2001][2001];
int main()
{
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++)
    {
        f[1][i]=1;
    }
    for(int i=1;i<=k;i++)
        for(int j=1;j<=n;j++)
            for(int t=j;t<=n;t=t+j)
    {
        f[i][t]=(f[i][t]+f[i-1][j])%pp;
    }
    long long ans=0;
    for(int i=1;i<=n;i++)
    {
        ans=ans+f[k][i];
        ans=ans%pp;
    }
    cout<<ans<<endl;
    return 0;
}

Alex doesn’t like boredom. That’s why whenever he gets bored, he comes up with games. One long winter evening he came up with a game and decided to play it.

Given a sequence a consisting of n integers. The player can make several steps. In a single step he can choose an element of the sequence (let’s denote it ak) and delete it, at that all elements equal to ak + 1 and ak - 1 also must be deleted from the sequence. That step brings ak points to the player.

Alex is a perfectionist, so he decided to get as many points as possible. Help him.

Input
The first line contains integer n (1 ≤ n ≤ 105) that shows how many numbers are in Alex’s sequence.

The second line contains n integers a1, a2, …, an (1 ≤ ai ≤ 105).

Output
Print a single integer — the maximum number of points that Alex can earn.

Examples
Input
2
1 2
Output
2
Input
3
1 2 3
Output
4
Input
9
1 2 1 3 2 2 2 2 3
Output
10
Note
Consider the third test example. At first step we need to choose any element equal to 2. After that step our sequence looks like this [2, 2, 2, 2]. Then we do 4 steps, on each step we choose any element equals to 2. In total we earn 10 points.
当前的要么已被带走要么没被带走两种情况要大的那个，f【i-1】和f【i-2】+相同数个数*该数数值；

#include <iostream>
using namespace std;
int main()
{
    long long t[100001]={0};
    long long f[100001]={0};
    int n;
    cin>>n;
    int a;
    int mm=0;
    for(int i=1;i<=n;i++)
    {
        cin>>a;
        t[a]++;
        if(a>mm) mm=a;
    }
    f[1]=t[1]*1;
    for(int i=2;i<=mm;i++)
    {
        f[i]=max(f[i-1],f[i-2]+t[i]*i);
    }
    cout<<f[mm]<<endl;
    return 0;
}

A string is binary, if it consists only of characters “0” and “1”.

String v is a substring of string w if it has a non-zero length and can be read starting from some position in string w. For example, string “010” has six substrings: “0”, “1”, “0”, “01”, “10”, “010”. Two substrings are considered different if their positions of occurrence are different. So, if some string occurs multiple times, we should consider it the number of times it occurs.

You are given a binary string s. Your task is to find the number of its substrings, containing exactly k characters “1”.

Input
The first line contains the single integer k (0 ≤ k ≤ 106). The second line contains a non-empty binary string s. The length of s does not exceed 106 characters.

Output
Print the single number — the number of substrings of the given string, containing exactly k characters “1”.

Please do not use the %lld specifier to read or write 64-bit integers in С++. It is preferred to use the cin, cout streams or the %I64d specifier.

Examples
Input
1
1010
Output
6
Input
2
01010
Output
4
Input
100
01010
Output
0
Note
In the first sample the sought substrings are: “1”, “1”, “10”, “01”, “10”, “010”.

In the second sample the sought substrings are: “101”, “0101”, “1010”, “01010”.
从前往后找0100011111101111001，找有两个一的情况，把对应状态写出来。

#include <iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n;
char b[1000001];
int f[1000001];
int main()
{
    int n;
    cin>>n;
    scanf("%s",b+1);
    int len=strlen(b+1);
    int op=0;
    long long ans=0;
    f[0]=1;
    for(int i=1;i<=len;i++)
    {
        if(b[i]=='1') op++;
            if(op>=n) ans=ans+f[op-n];
            f[op]++;
    }
    cout<<ans<<endl;
    return 0;
}

Tsumugi brought n delicious sweets to the Light Music Club. They are numbered from 1 to n, where the i-th sweet has a sugar concentration described by an integer ai.

Yui loves sweets, but she can eat at most m sweets each day for health reasons.

Days are 1-indexed (numbered 1,2,3,…). Eating the sweet i at the d-th day will cause a sugar penalty of (d⋅ai), as sweets become more sugary with time. A sweet can be eaten at most once.

The total sugar penalty will be the sum of the individual penalties of each sweet eaten.

Suppose that Yui chooses exactly k sweets, and eats them in any order she wants. What is the minimum total sugar penalty she can get?

Since Yui is an undecided girl, she wants you to answer this question for every value of k between 1 and n.

Input
The first line contains two integers n and m (1≤m≤n≤200 000).

The second line contains n integers a1,a2,…,an (1≤ai≤200 000).

Output
You have to output n integers x1,x2,…,xn on a single line, separed by spaces, where xk is the minimum total sugar penalty Yui can get if she eats exactly k sweets.

Examples
Input
9 2
6 19 3 4 4 2 6 7 8
Output
2 5 11 18 30 43 62 83 121
Input
1 1
7
Output
7
Note
Let’s analyze the answer for k=5 in the first example. Here is one of the possible ways to eat 5 sweets that minimize total sugar penalty:

Day 1: sweets 1 and 4
Day 2: sweets 5 and 3
Day 3 : sweet 6
Total penalty is 1⋅a1+1⋅a4+2⋅a5+2⋅a3+3⋅a6=6+4+8+6+6=30. We can prove that it’s the minimum total sugar penalty Yui can achieve if she eats 5 sweets, hence x5=30.
暴力搜索

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
int a[200001];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    sort(a+1,a+1+n);
    for(int i=1;i<=n;i++)
    {
        int j=i;
        int ans=0;
        int k=1;
        while(1)
        {
            int l=m;
            //if(i>=m)
            while(l--)
            {
                ans=ans+a[j]*k;
                j--;
                if(j==0)break;
            }
            k++;
            if(j==0) break;
        }
        printf("%d ",ans);
    }
    return 0;
}

前缀化爆搜

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
long long a[200001];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
            scanf("%d",&a[i]);
            sort(a+1,a+1+n);
    for(int i=1;i<=n;i++)
        a[i]=a[i-1]+a[i];
        for(int i=1;i<=n;i++)
        {
            int j=i;
            long long ans=0;
            int k=1;
            while(j>=m)
             {
                 ans=ans+(a[j]-a[j-m])*k;
                 j=j-m;
                 k++;
             }
             ans=ans+a[j]*k;
            printf("%lld ",ans);
        }
    return 0;
}

dp
把第一个测试数据的九个数改成123456789；从前往后写所要的值。

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
long long a[200001];
long long f[200001];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
            scanf("%d",&a[i]);
            sort(a+1,a+1+n);
    for(int i=1;i<=n;i++)
        a[i]=a[i-1]+a[i];
        for(int i=1;i<=n;i++)
        {
            if(i<m) {f[i]=a[i];printf("%lld ",f[i]);}
            else
            {
                f[i]=f[i-m]+a[i];
                printf("%lld ",f[i]);
            }
        }
    return 0;
}

You are given a tetrahedron. Let’s mark its vertices with letters A, B, C and D correspondingly.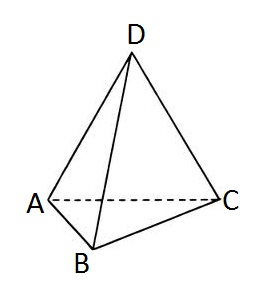 在这里插入图片描述

An ant is standing in the vertex D of the tetrahedron. The ant is quite active and he wouldn’t stay idle. At each moment of time he makes a step from one vertex to another one along some edge of the tetrahedron. The ant just can’t stand on one place.

You do not have to do much to solve the problem: your task is to count the number of ways in which the ant can go from the initial vertex D to itself in exactly n steps. In other words, you are asked to find out the number of different cyclic paths with the length of n from vertex D to itself. As the number can be quite large, you should print it modulo 1000000007 (109 + 7).

Input
The first line contains the only integer n (1 ≤ n ≤ 107) — the required length of the cyclic path.

Output
Print the only integer — the required number of ways modulo 1000000007 (109 + 7).

Examples
Input
2
Output
3
Input
4
Output
21
Note
The required paths in the first sample are:

D - A - D
D - B - D
D - C - D
把前四种情况写出来看看数与数之间的关系，胡蒙瞎猜，再把猜想放到图形中试一试结合着概率乘积看一看是否感觉上合理。感觉规律不是很复杂。

#include <iostream>
using namespace std;
const int k=1e9+7;
long long f[10000001];
int main()
{
    int n;
    cin>>n;
    f[1]=0;
    f[2]=3;
    for(int i=3;i<=n;i++)
    {
        f[i]=(f[i-1]*2+f[i-2]*3)%k;
    }
    cout<<f[n]<<endl;
    return 0;
}