引:
决策树是一个预测模型,他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度,使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。
构造决策树的基本思想(大众化表述):为的是随着树深度的增加,节点的熵迅速的降低(熵值越低,节点越纯)。熵降低的速度越快越好,这样才能有望得到一颗高度尽可能矮的决策树。
几个概念的引出:

P(几率越大)==》H(X)值越小 P(几率越小)==》H(X)值越大
1.算法基本流程:
以下是决策树学习基本算法流程:

2. 主题框架
2.1 信息熵
信息熵:描述一个事物/集合的不确定性。不确定性大 ==》熵值大。
信息熵可以作为衡量一个模型的标准。信息熵越小,代表当前的类别是比较纯的(纯度较大)。
![]() 之所以用累加符号,是为了计算整个集合的信息熵,而不是单独某个元素的。
之所以用累加符号,是为了计算整个集合的信息熵,而不是单独某个元素的。
比如说:【 假设 A=[1,3,6,4,3],集合B=[1,1,1,2,1] 】。 若A集合其内部种类比较多,则其每一种元素取到的概率P(x)就较小,则此集合的信息熵较大! B集合其内部种类比较少,则其每一种元素取到的概率P(x)就较大,则此集合的信息熵较小!
2.2 ID3:信息增益(传统算法)
信息增益:信息熵 - 使用?属性对集合划分后的熵。
ID3决策树学习算法就是一信息增益为准则,进行决策树的属性划分。同样的方式可以计算出其他特征的信息增益,那么我们选择最大的那个就可以啦,相当于是遍历了一遍特征,找出来了大当家,然后再其余的中继续通过信息增益找二当家!

存在问题:
若是以 ID 最为特征(有多少元素就代表多少个属性。),则其熵值计算下来就会是 0 。!也就是说,Gain(D,a)在这种情况下会最大化。【现在的划分情况是 高度为 2 的多分支树】
针对此问题,我们进一步提出了信息增益率这一概念,如下:
2.3 C4.5:信息增益率
信息增益率:当前所选节点下的信息增益 / 自身的熵值。 哈哈哈,妙哉!!!则这种情况下,分子(信息增益)虽然是较大了,但其分母(自身熵)更是大的可怕。最终导致增益率非常之小,也就解决了上面那个问题。


2.4 CART:基尼(Gini)系数(描述分类效果)
![]()
对于实际概率与该系数的关系,基本也与信息熵的大略相近。也是概率越大对应的基尼系数就越小。咱们需要 注意的就是先记住它。基尼系数越小,代表当前的类别是比较纯的(纯度较大)。另外需要注意的是考虑累加符号,是为了把当前类别 的每一种元素都考虑进来。
2.5 评价函数:  (希望其越小越好,类似损失函数)
(希望其越小越好,类似损失函数)
这里的 t属于leaf ,代表这里考虑的都是叶子节点。其中: 代表当前的叶子节点有多少个样本。H(t) 代表该叶子节点的熵值或基尼系数值。
引例:
上例子来解释以上枯燥理论的具体应用:{本例摘选自唐宇迪老师PPT}
对于一个待处理的数据集如下图所示,考虑用以下数据来作为数据源构建一颗决策树,用于根据如下列举各因素预测是否满足play(play代表打球)的条件。
对于以上的数据,如果我们要构建一颗树,该如何下手去选择根节点呢(因为我们的选择不唯一嘛)?可做的几个选择如下图示:
在没有给定任何天气信息时,根据历史数据,我们只知道新的一天打球的概率是9/14,不打的概率是5/14。此时的熵为:
由此,我们可以分别计算另外几个属性的各个信息熵的值:
3.剪枝处理:
3.1 预剪枝
剪枝(pruning)是决策树学习算法对付“过拟合”的主要手段.在决策树学习中,为了尽可能正确分类训练样本,结点划分过程将不断重复,有时会造成决策树分支过多,这时就可能因训练样本学得“太好”了,以致于把训练集自身的一些特点当作所有数据都具有的一般性质而导致过拟合.因此,可通过主动去掉一些分支来降低过拟合的风险.
决策树剪枝的基本策略有“预剪枝”(prepruning)和“后剪枝”(post-pruning)。预剪枝是指在决策树生成过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶结点;后剪枝则是先从训练集生成一棵完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶结点。


对比图4.6和图4.5可看出,预剪枝使得决策树的很多分支都没有“展开”,这不仅降低了过拟合的风险,还显著减少了决策树的训练时间开销和测试时间开销。但另一方面,有些分支的当前划分虽不能提升泛化性能、甚至可能导致泛化性能暂时下降,但在其基础上进行的后续划分却有可能导致性能显著提高;
预剪枝基于“贪心”本质禁止这些分支展开,给预剪枝决策树带来了欠拟合的风险.
3.2 后剪枝


对比图4.7和图4.6可看出,后剪枝决策树通常比预剪枝决策树保留了更多的分支。一般情形下,后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树.但后剪枝过程是在生成完全决策树之后进行的。并且要自底向上地对树中的所有非叶结点进行逐一考察,因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多
4.连续与缺失值:
4.1连续值处理
由于连续属性的可取值数目不再有限,因此,不能直接根据连续属性的可取值来对结点进行划分.此时,连续属性离散化技术可派上用场.最简单的策略是采用二分法(bi-partition)对连续属性进行处理,这正是C4.5决策树算法中采用的机制。
4.2缺失值处理
现实任务中常会遇到不完整样本,即样本的某些属性值缺失。例如由于诊测成本、隐私保护等因素,患者的医疗数据在某些属性上的取值(如HIV测试结果)未知。尤其是在属性数目较多的情况下,往往会有大量样本出现缺失值.如果简单地放弃不完整样本,仅使用无缺失值的样本来进行学习,显然是对数据的极大浪费。
我们需解决两个问题:(1)如何在属性值缺失的情况下进行划分属性选择?(2)给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分?
5.多变量决策树:
参考文献:
《机器学习》——周志华
【机器学习算法课程】—— 唐宇迪
最后
以上就是伶俐毛豆最近收集整理的关于【ML_Algorithm 4 】决策树(Decision Tree)——算法概念梳理的全部内容,更多相关【ML_Algorithm内容请搜索靠谱客的其他文章。


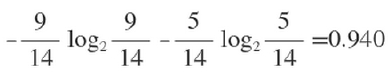










发表评论 取消回复