2 机械臂基础
- 3.3 机械臂建模
- 3.3.1 利用DH参数建立机械臂模型
- 3.3.2对机械臂正逆运动求解
3.3 机械臂建模
3.3.1 利用DH参数建立机械臂模型
Step1：确定DH参数，使用Link函数创建关节。DH参数包括：theta、d、a和alpha即对应关节角、连杆偏距、连杆长度和连杆转角。利用函数Link创建DH参数的连杆：连杆名称=Link([theta,d,a,alpha])。
创建完的连杆可以进行的一些操作：
①获取连杆关节类型：连杆名称.RP；
②获取连杆关节角：连杆名称.theta；
③获取连杆偏距：连杆名称.d；
④获取连杆长度：连杆名称.a；
⑤获取连杆扭转角：连杆名称.alpha。
Step2:利用SerialLink函数将连杆连接成机械臂：机械臂名称=SerialLink(连杆序列名1…)。
创建完的机械臂可以进行的一些操作：
①显示机械臂模型：机械臂名称.display；
②示教模式显示机械臂：机械臂名称.teach；
③显示机械臂关节类型：机械臂名称.config；
④显示机械臂DH矩阵：机械臂名称.mdh；
⑤显示机械臂关节极限位置：机械臂名称.qlim；
⑥显示机械臂末端与基座变换矩阵：机械臂名称.tool
例子1：创建一个简单的RRRRRR机械臂
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
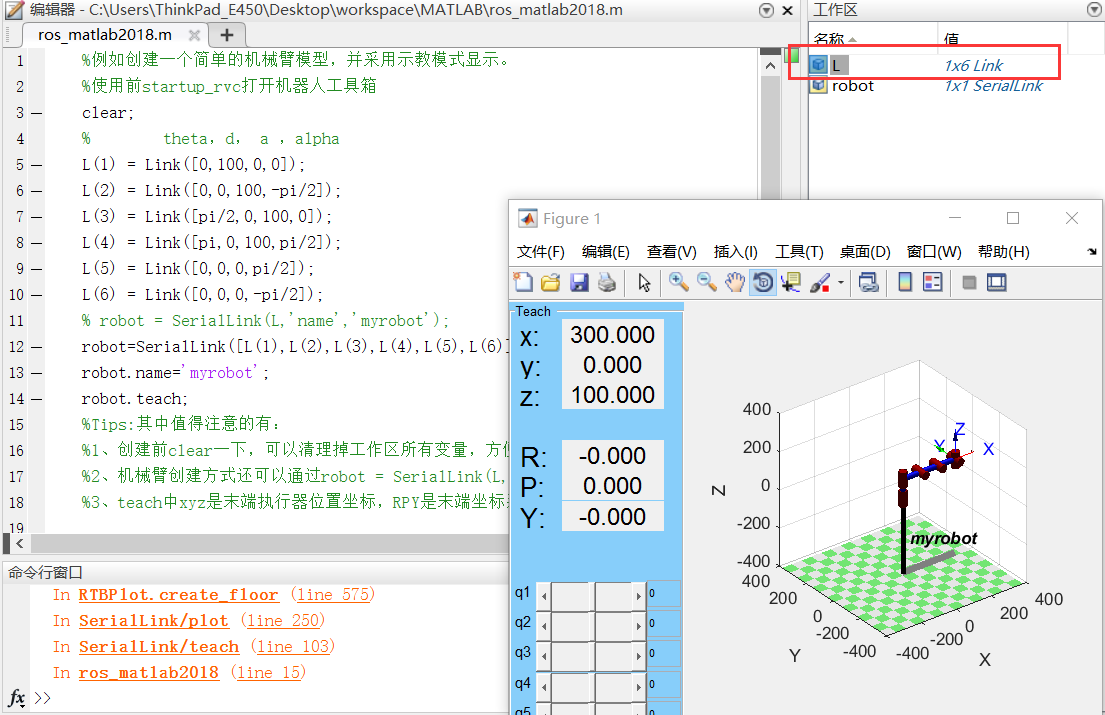
19%例如创建一个简单的机械臂模型，并采用示教模式显示。 %使用前startup_rvc打开机器人工具箱 clear; % theta，d， a ，alpha L(1) = Link([0,100,0,0]); L(2) = Link([0,0,100,-pi/2]); L(3) = Link([pi/2,0,100,0]); L(4) = Link([pi,0,100,pi/2]); L(5) = Link([0,0,0,pi/2]); L(6) = Link([0,0,0,-pi/2]); % robot = SerialLink(L,'name','myrobot'); robot=SerialLink([L(1),L(2),L(3),L(4),L(5),L(6)]); robot.name='myrobot'; robot.teach; %Tips:其中值得注意的有： %1、创建前clear一下，可以清理掉工作区所有变量，方便理解L(1)和robot变量的含义 %2、机械臂创建方式还可以通过robot = SerialLink(L,'name','myrobot');其中L很特殊(看看工作空间) %3、teach中xyz是末端执行器位置坐标，RPY是末端坐标系姿态(俯仰、横滚、偏航)
例子2：创建一个简单的RPR机械臂，限制运动位置和显示空间
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
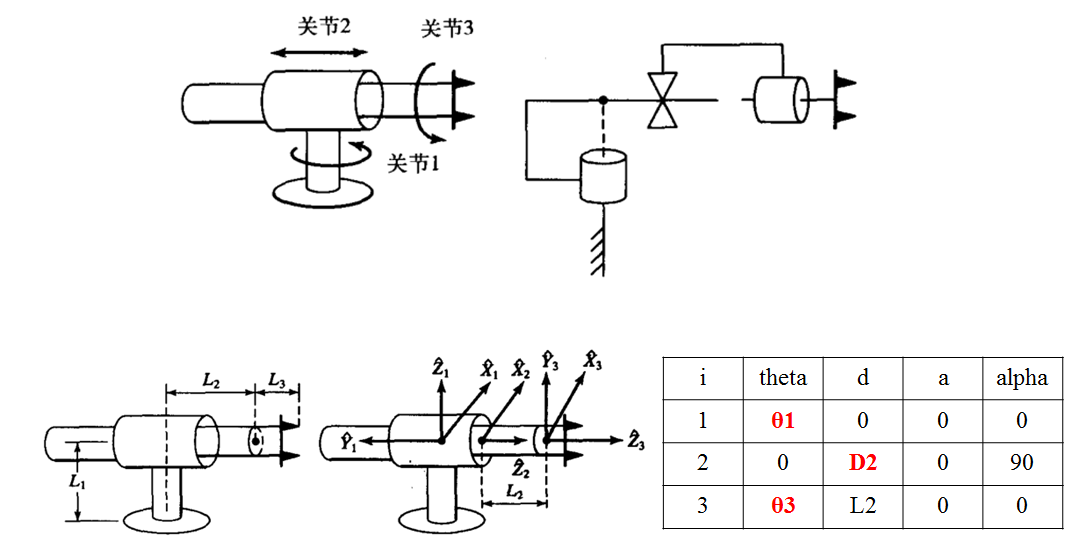
29%创建一个简单的的RPR型机械臂，并限制移动位置和显示空间 %使用前startup_rvc打开机器人工具箱 clear; %分析DH的4个参数，变量可以模糊定义 %L(1)中的theta可以模糊定义，L(2)中d模糊定义，L(3)中theta模糊定义 %定义方式1： % L(1) = Link('qlim',[-pi,pi], 'd',0, 'a',0, 'alpha',0); % L(2) = Link('theta',0, 'qlim',[0,30], 'a',0, 'alpha',pi/2); % L(3) = Link('qlim',[-pi,pi], 'd',10, 'a',0, 'alpha',0); % %定义方式2： % L(1) = Link('qlim',[-pi,pi], 'd',0, 'a',0, 'alpha',0, 'standard'); % L(2) = Link('theta',0, 'qlim',[0,30], 'a',0, 'alpha',pi/2, 'standard'); % L(3) = Link('qlim',[-pi,pi], 'd',10, 'a',0, 'alpha',0, 'standard'); %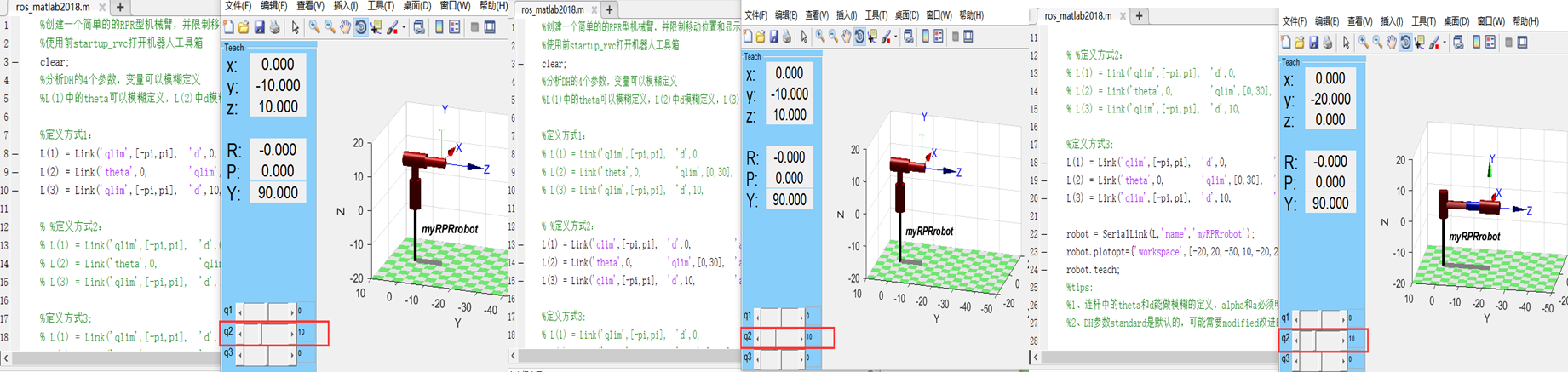定义方式3: L(1) = Link('qlim',[-pi,pi], 'd',0, 'a',0, 'alpha',0, 'modified'); L(2) = Link('theta',0, 'qlim',[0,30], 'a',0, 'alpha',pi/2, 'modified'); L(3) = Link('qlim',[-pi,pi], 'd',10, 'a',0, 'alpha',0, 'modified'); robot = SerialLink(L,'name','myRPRrobot'); robot.plotopt={'workspace',[-20,20,-50,10,-20,20]}; robot.teach; %tips: %1、连杆中的theta和d能做模糊的定义，alpha和a必须明确的定义 %2、DH参数standard是默认的，有时候需要modified即改进的DH方法
3.3.2对机械臂正逆运动求解
（一）正运动学函数fkine：返回变量=机械臂名.fkine([关节参数1 关节参数2….])。其中返回变量存在t、o、a和n四个指令。正运动学在已知关节参数的情况下可以求出末端相对于基准的变化矩阵，间接求得末端位置再基准坐标的坐标值。因此可以利用正运动学函数fkine求解工作空间。
例1：对3.2.1得到的RPR机械臂进行正运动学求解工作空间。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41clear; L(1) = Link('d',0, 'a',0, 'alpha',0, 'modified'); L(2) = Link('theta',0, 'a',0, 'alpha',pi/2, 'modified'); L(3) = Link( 'd',10, 'a',0, 'alpha',0, 'modified'); stfrpr = SerialLink(L,'name','stfRPR'); L(1).qlim=[-pi,pi]; L(3).qlim=[-pi,pi]; L(2).qlim=[0,30]; % %使用for循环开销太大 % for i=-pi:pi/36:pi % for j=0:1:30 % for k=-pi:pi/0.36:pi % pp=stfrpr.fkine([i j k]); % plot3(pp.t(1),pp.t(2),pp.t(3),'b.','MarkerSize',5); % hold on % end % end % end %N的数值决定theta的范围 N=5000; theta1=-pi+2*pi*rand(N,1); d2=0+30*pi*rand(N,1); theta3=-pi+2*pi*rand(N,1); %循环的n决定绘图的点数个数 for n=1:1:3000 pp=stfrpr.fkine([theta1(n) d2(n) theta3(n)]); plot3(pp.t(1),pp.t(2),pp.t(3),'b.','MarkerSize',5); %hold on暂停窗口，使得for n=1:1:3000的点按循环全部绘制在一个窗口 hold on end %Tips: %1、利用for循环求解机械臂工作空间开销太大； %2、随机函数N决定theta角度的离散数值范围，rand(N,1)表示新建N个0~1的随机数，1表示1列，如果1改成10则是10列数，每列都是N个。如在theta1中用qlim限制为[-pi,pi]那么为了使得离散的theta1也在[-pi,pi]之间，因此其值为-pi+2*pi*rand(N,1)。得出结论X.qlim=[a,b]时，则离散范围X=a+(b-a)*rand(N,1)； %3、for循环的n表示绘制点图时点的个数； %4、hold on表示暂停窗口，使得点全部在一个窗口上显示。
结果为：
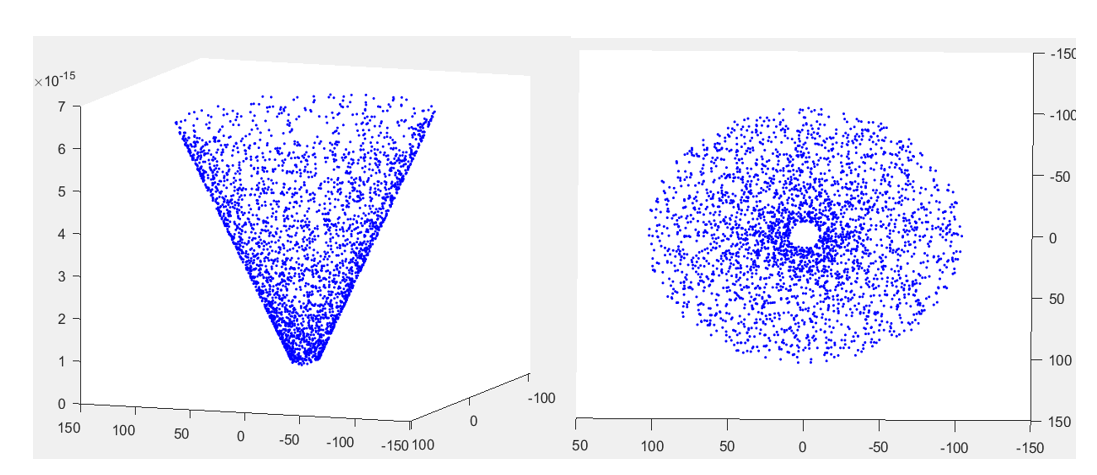
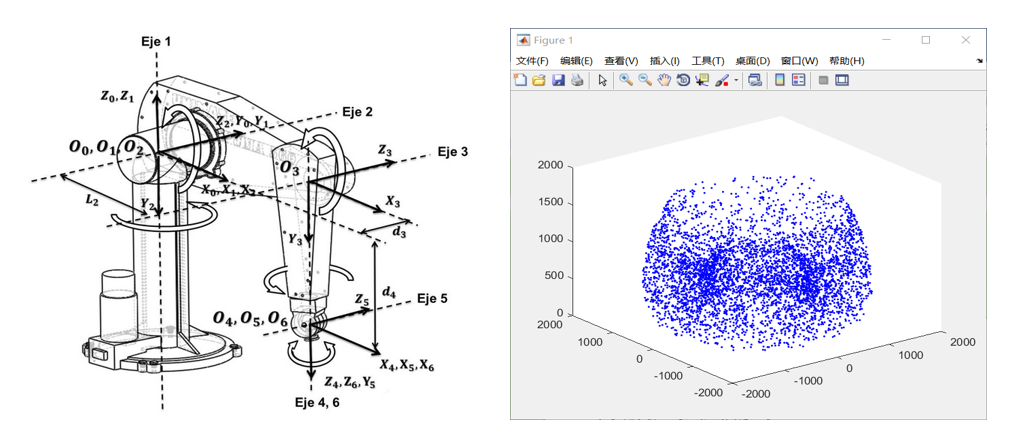
例2：对PUMA560机械臂建模求解工作空间
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29clear; L(1) = Link( 'd',500, 'a',0, 'alpha',pi/2); L(2) = Link( 'd',0, 'a',1250, 'alpha',0); L(3) = Link( 'd',0, 'a',0, 'alpha',pi/2); L(4) = Link( 'd',500, 'a',0, 'alpha',pi/2); L(5) = Link( 'd',0, 'a',0, 'alpha',-pi/2); L(6) = Link( 'd',0, 'a',0, 'alpha',0); L(2).qlim=[0,pi/4]; L(3).qlim=[-pi/2,pi/2]; pm = SerialLink(L,'name','puma560'); % pm.teach N=5000; theta1=-pi+2*pi*rand(N,1); theta2=pi/4*rand(N,1); theta3=-pi/2+pi*rand(N,1); theta4=-pi+2*pi*rand(N,1); theta5=-pi+2*pi*rand(N,1); theta6=-pi+2*pi*rand(N,1); for n=1:1:5000 pp=pm.fkine([theta1(n) theta2(n) theta3(n) theta4(n) theta5(n) theta6(n)]); plot3(pp.t(1),pp.t(2),pp.t(3),'b.','MarkerSize',5); hold on end
（二）逆运动学函数ikine：返回变量=机械臂名.ikine(变化矩阵)。逆运动学是已知变化矩阵得出关节参数，因此对ikine函数的返回变量进行变化得到关节参的参考值，但是ikine函数只能返回一组解，因此想要全部的逆解还是得编写.m文件计算。
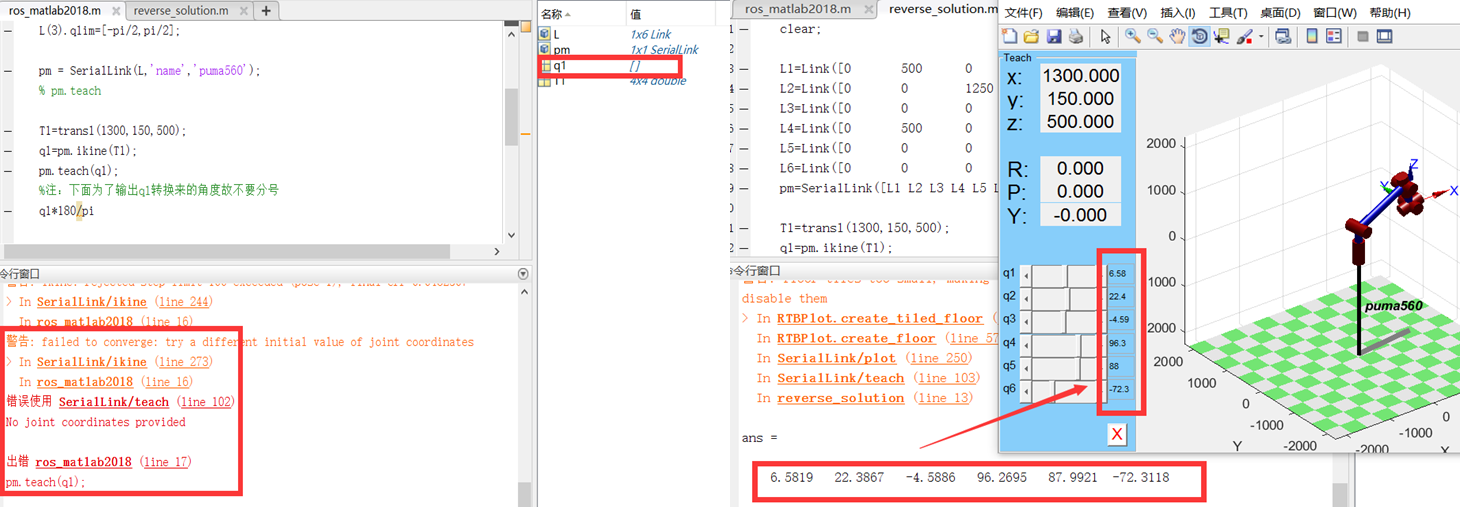
例1：对正运动学中创建的PUMA560求解其末端位置在[1300,150,500]的返回的关节参数。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56%DH参数定义不一样，效果不一样 %DH定义1，此时的ikine求不出逆解 clear; L(1) = Link( 'd',500, 'a',0, 'alpha',pi/2); L(2) = Link( 'd',0, 'a',1250, 'alpha',0); L(3) = Link( 'd',0, 'a',0, 'alpha',pi/2); L(4) = Link( 'd',500, 'a',0, 'alpha',pi/2); L(5) = Link( 'd',0, 'a',0, 'alpha',-pi/2); L(6) = Link( 'd',0, 'a',0, 'alpha',0); L(2).qlim=[0,pi/4]; L(3).qlim=[-pi/2,pi/2]; pm = SerialLink(L,'name','puma560'); % pm.teach T1=transl(1300,150,500); q1=pm.ikine(T1); pm.teach(q1); %注：下面为了输出ql转换来的角度故不要分号 q1*180/pi %DH参数定义2，此时theta给直接赋予初始值0，这是可以求解出ikine在[1300,150,500]的参数 clear; L1=Link([0 500 0 pi/2 0 ]); L2=Link([0 0 1250 0 0 ]); L3=Link([0 0 0 pi/2 0 ]); L4=Link([0 500 0 pi/2 0 ]); L5=Link([0 0 0 -pi/2 0 ]); L6=Link([0 0 0 pi/2 0 ]); pm=SerialLink([L1 L2 L3 L4 L5 L6],'name','puma560'); T1=transl(1300,150,500); q1=pm.ikine(T1); pm.teach(q1); %注：下面为了输出ql转换来的角度故不要分号 q1*180/pi %Tips: %1、由于ikine函数需要末端和基准的变化矩阵，因此假设基准坐标系就是teach界面显示 % 的全局坐标系，当确定了末端的位置就可以通过transl平移函数得到变化矩阵，由于只 % 是平移得来的变化矩阵，这样末端位置的位姿(坐标系的方向)始终和基准坐标系保持一 % 致。利用trotx函数变化位姿。 %2、关于位姿：例如本例中的机器人默认状态(六个角度都是0)末端位置为[1250,0,0]这时候的 %末端XYZ与基准方向都不一致()!!!当theta1旋转90度后，坐标为[0,1250,0]机械臂可达但此时 %位姿XYZ与基准XYZ不一致！！！想用transl(0,1250,0)肯定报错！！！ %3、由于ikine计算方式，因此指定了坐标也不一定能够求出解(如DH定义不一样，可能影响末端的位姿状态所有就有些得不到逆解)
上一篇：3 Robotics Toolbox（1---安装与坐标变换）
最后
以上就是腼腆黑夜最近收集整理的关于2 机械臂基础（2---Robotics Toolbox对机械臂建模、正逆运动求解）3.3 机械臂建模的全部内容，更多相关2内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复