教你用matlab快速解决烦人的符号变换（Fourier、Laplace和 z 变换）和符号卷积符号变换符号卷积备注

83 阅读 0 评论 55 点赞

我是靠谱客的博主俊秀荷花，最近开发中收集的这篇文章主要介绍教你用matlab快速解决烦人的符号变换（Fourier、Laplace和 z 变换）和符号卷积符号变换符号卷积备注，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

符号变换

Fourier变换及其反变换

Laplace变换及其反变换

Z变换及其反变换

符号卷积

备注

符号变换

Fourier变换及其反变换

fourier()是算符号表达式的傅里叶变换的，算出来结果要画图可以用ezplot();

【例 1】求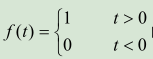的 Fourier 变换。

matlab 代码：

% 傅里叶变换
syms t w
ut=heaviside(t);
UT=fourier(ut)
% 结果
UT =
pi*dirac(w)-i/w

% 傅里叶反变换
Ut=ifourier(UT,w,t)
% 结果
Ut =
heaviside(t)

【例 2】根据 Fourier 变换定义，用积分指令求方波脉冲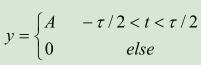的Fourier 变换。

% 傅里叶变换
syms A t w
syms tao positive
yt=heaviside(t+tao/2)-heaviside(t-tao/2);
Yw=fourier(A*yt,t,w)
% 结果
Yw =
2*A/w*sin(1/2*tao*w)

% 傅里叶反变换
Yt=ifourier(Yw,w,t)
% 结果
Yt =
A*(heaviside(t+1/2*tao)-heaviside(t-1/2*tao))

% 画图
yt3=subs(yt,tao,3)
Yw3=subs(Yw,[A,tao],[1,3])
subplot(2,1,1)
Ht=ezplot(yt3,[-3,3]);
set(Ht,'Color','r','LineWidth',3)
subplot(2,1,2),ezplot(Yw3)
% 输出结果
yt3 =
heaviside(t+3/2)-heaviside(t-3/2)
Yw3 =
2/w*sin(3/2*w)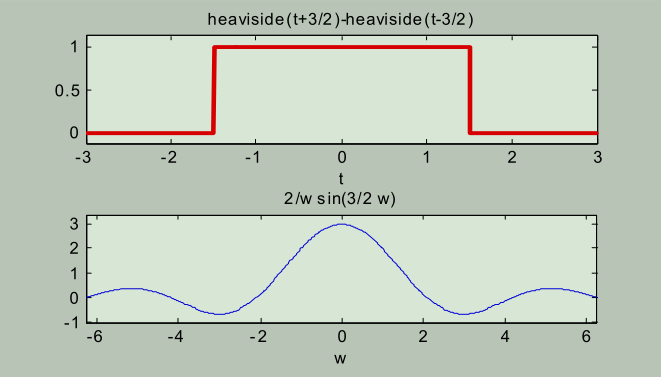

Laplace变换及其反变换

1、拉普拉斯（laplace）变换

语法：F= laplace(f,t,s) %求时域函数f（t）的laplace变换F

说明：F是s的函数，参数s省略，返回结果F默认为’s’的函数；f为t的函数，当参数t省略，默认自由变量为’t’。

【例1】求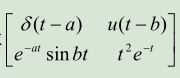的 Laplace 变换。

% Laplace变换
syms t s;
syms a b positive  
Dt=dirac(t-a); 
Ut=heaviside(t-b); 
Mt=[Dt,Ut;exp(-a*t)*sin(b*t),t^2*exp(-t)];
MS=laplace(Mt,t,s)
% 结果
MS =
[ exp(-s*a), exp(-s*b)/s]
[ 1/b/((s+a)^2/b^2+1), 2/(s+1)^3]

2、拉普拉斯（laplace）反变换

语法：F=i laplace(f,t,s) %求F的laplace反变换f

【例2】求1/(s+a)和1函数的laplace反变换

% 1/(s+a)函数的laplace反变换
syms a t s
f1=ilaplace(1/(s+a),s,t) %求1/(s+a)函数的laplace反变换
% 1函数的laplace反变换
f2=ilaplace(1,s,t) %求1函数的laplace反变换是脉冲函数dirac(t)
% 结果
f1 =
    exp(-a*t)

f2 =
    dirac(t)

【例 3】验证 Laplace 时移性质：。

% 代码
syms t s
syms t0 positive
ft=sym('f(t-t0)')*heaviside(t-t0)
FS=laplace(ft,t,s)
FS_t=ilaplace(FS,s,t)
% 结果
ft =
f(t-t0)*heaviside(t-t0)
FS =
exp(-s*t0)*laplace(f(t),t,s)
FS_t =
f(t-t0)*heaviside(t-t0)

Z变换及其反变换

1、z变换ztrans

单位阶跃函数：f(t)=1（t）

采样值f(nT)=1

clc,clear;
syms  z
f=1;
ztrans(f,z)%'f'是单位阶跃函数，'z'是z函数的变量

单位阶跃函数：

clc,clear
syms  a b t z
f=1/(a-b)*(exp(-(b*t))-exp(-a*t));
ztrans(f)

2、z反变换iztrans

clc,clear
syms n  z
f=1;
F=ztrans(f,n,z);
iztrans(F,z,n)

【例 2.5-6】求序列 的 Z 变换，并用反变换验算。

% z变换
syms n
Delta=sym('charfcn[0](n)'); %  <2>
D0=subs(Delta,n,0); %
D15=subs(Delta,n,15);  %
disp('[D0,D15]');disp([D0,D15])
% 结果
[D0,D15]
[ 1, 0]
% z反变换
syms z
fn=2*Delta+6*(1-(1/2)^n)
FZ=simple(ztrans(fn,n,z));
disp('FZ = ')
pretty(FZ)
FZ_n=iztrans(FZ,z,n)
% 结果
fn =
2*charfcn[0](n)+6-6*(1/2)^n
FZ =
          2
        4 z + 2
    --------------
          2
     2 z - 3 z + 1
FZ_n =
2*charfcn[0](n)+6-6*(1/2)^n

符号卷积

【例 1】已知系统冲激响应输入下的输出响应。

% 变换
syms T t tao
ut=exp(-t); 
ht=exp(-t/T)/T; 
uh_tao=subs(ut,t,tao)*subs(ht,t,t-tao); 
yt=simple(simple(int(uh_tao,tao,0,t)))
% 结果
yt =
-(exp(-t)-exp(-t/T))/(T-1)

【例 2】采用 Laplace 变换和反变换求上例的输出响应。

% 代码
syms s
yt=ilaplace(laplace(ut,t,s)*laplace(ht,t,s),s,t);
yt=simple(yt)
% 结果
yt =
(-exp(-t)+exp(-t/T))/(T-1)

【例 2.5-9】求函数和的卷积。

% 代码
syms tao
t=sym('t','positive'); 
ut=heaviside(t)-heaviside(t-1);
ht=t*exp(-t);
yt=int(subs(ut,t,tao)*subs(ht,t,t-tao),tao,0,t)
yt=collect(yt,'heaviside(t-1)')
% 结果
yt =
1+t*heaviside(t-1)*exp(1-t)-heaviside(t-1)+(-t-1)/exp(t)
yt =
(exp(1-t)*t-1)*heaviside(t-1)+1+(-t-1)/exp(t)