基于Matlab的SVD信号去噪方法应用

                    目录

1.题目

2.方法

3.程序

4.分析

5.结论

1.题目

使用Matlab，研究SVD去噪的方法。构造一个含有噪声的一维数组，将SVD用于一维信号的去噪。

2.方法

将Hankel矩阵中的特征值降序排列，把反映主要噪声的奇异值置零，就可以去除信号中的噪声。

3.程序

clear all; clc;
t=0:0.1:6.3;
x= 10.*sin(t)+2.*cos(2.*t); % 构造一个原始信号
noise=unifrnd(-1,1,1,64);  % 构造噪声
y=x+noise;                  % 最终信号
y1=reshape(y,8,8);         % 信号y只有1行，没法进行SVD分解，所以先改变一下形状，
[u s v]=svd(y1);            % 对y1进行SVD分解，s为包含奇异值的矩阵
s1=s;u1=u;v1=v;
% 令第3到8个奇异值为0，u,v也要相应变化
s1(3:8,3:8)=0;            
u1(8,8)=0; u1(7,7)=0; u1(6,6)=0; u1(5,5)=0; u1(4,4)=0; u1(3,3)=0; 
v1(8,8)=0; v1(7,7)=0; v1(6,6)=0; v1(5,5)=0; v1(4,4)=0; v1(3,3)=0; 
y2=u1*s1*v1';                % 重构信号，注意这里乘的是v1的转置
y2=reshape(y2,1,64);        % 不要忘了reshape一下
% 求Hankel矩阵的特征值
[x_Tezhenxiangliang,y_Tezhenzhi]=eig(s);
Tezhenzhi = sort(diag(y_Tezhenzhi),'descend');   %取对角元素，即矩阵的特征值

figure();
subplot(2,2,1);
plot(t,x,'k');  grid on;             
title('a.原始信号');
subplot(2,2,2);
plot(t,noise,'r'); grid on;          
title('b.噪声信号');
subplot(2,2,3);
plot(t,y,'k');grid on;
title('c.叠加噪声的信号');   
subplot(2,2,4);
plot(t,y2,'k');grid on;              
title('e.SVD去掉的噪声的信号');

figure();
for i = 1:8
    plot(i,Tezhenzhi(i,1),'k^');          
    hold on;
end
grid on;
title('d.Hankel矩阵的特征值');

4.分析

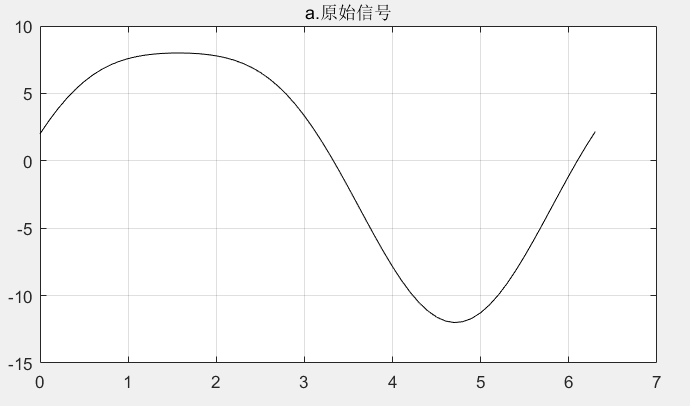
如图a所示，构造了一个平滑的原始信号。

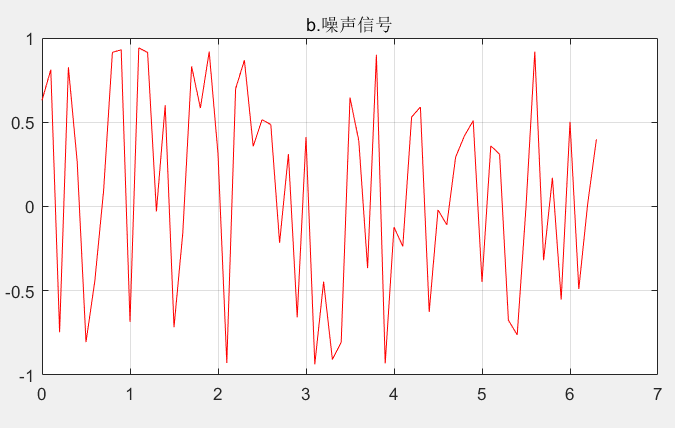
如图b所示，生成-1到1之间的噪声信号。

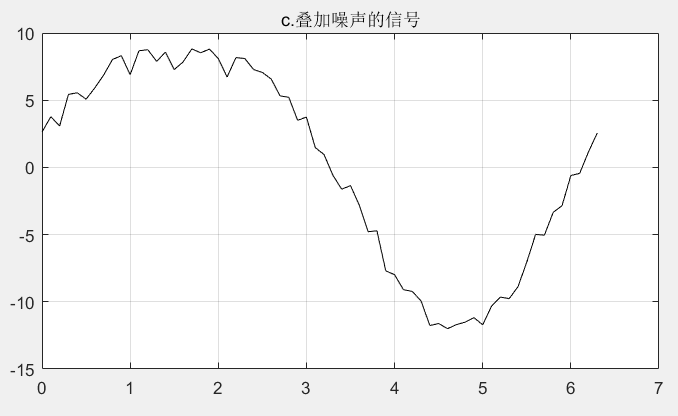
如图c所示，为原始信号叠加噪声后的信号。

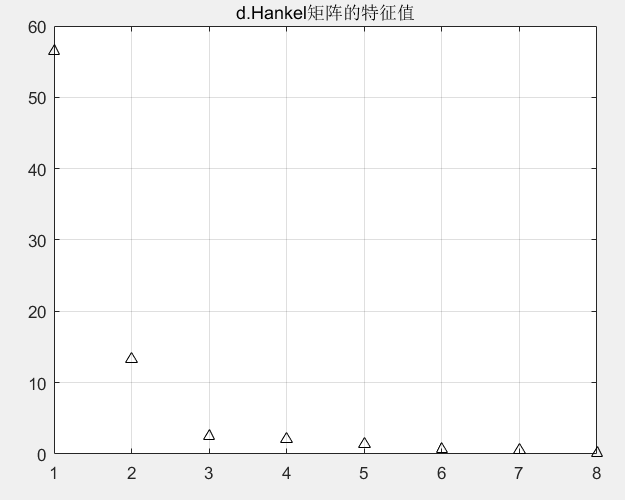
如图d所示，为SVD奇异值分解过程中，Hankel矩阵的特征值。根据特征值的大小分布，这里将反映主要噪声3-8位置的特征值置零。

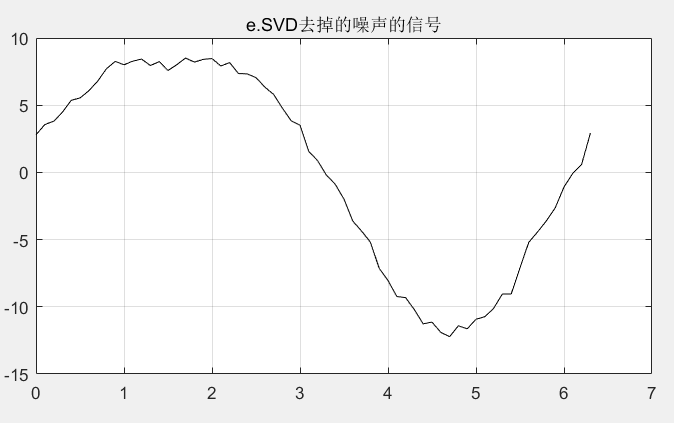
如图e所示，为经过SVD去噪后的信号。

5.结论

去噪信号图e和叠加噪声信号的图c对比，可观察到SVD去噪有一定的效果。

去噪信号图e和原始信号图a对比，可观察到去噪参数还有待进一步调整，才能达到更好的去噪效果。

最后

以上就是积极茉莉为你收集整理的基于Matlab的SVD信号去噪方法应用的全部内容，希望文章能够帮你解决基于Matlab的SVD信号去噪方法应用所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。