Graph Neural Networks—GCN、GraphSAGE、GAT
- GNN原始定义
- GCN
- GraphSAGE
- GAT
- GCN(1stChebNet)、GraphSAGE和GAT对比
- 谱域GCN和空域GCN对比
- 谱域GCN
- 空域GCN
- GCN和GraphSAGE对比
- 补充
GNN原始定义
传统的深度学习方法在提取欧氏空间的数据集上取得了巨大的成功,特别是像计算机视觉这类技术。传统的深度学习中,我们认为数据点之间没有显式的联系,但许多实际应用场景中的数据是非欧式的,也就是说,数据对象之间存在某种关系,如社交网络、交通网络等。这类数据其实可以看作一种图结构,传统的深度学习技术很难直接处理这类数据。主要有以下原因:
- 因为图是不规则的,每个图都有一个大小可变的无序节点,图中的每个节点都有不同数量的相邻节点,导致一些重要的操作(例如卷积)在图像(Image)上很容易计算,但不再适合直接用于图。
- 此外,现有深度学习算法的一个核心假设是数据样本之间彼此独立。然而,对于图来说,情况并非如此,图中的每个数据样本(节点)都会有边与图中其他实数据样本(节点)相关,这些信息可用于捕获实例之间的相互依赖关系。比如,化学中分子之间连接、社交网络中的朋友关系、知识图谱中实体与实体之间的关系、推荐系统中用户与项目之间的交互。
传统的深度学习技术通常将这种数据处理成欧式数据,然后作为模型的输入,这会造成信息的损失。因此,借助这些因素的推动,图神经网络(GNNs)应运而生。由于GNNs可以直接处理图网络数据,以及可以学习图的拓扑结构,因此它在处理结构化数据时显示出的强大传播能力和表达能力。
其实,GNN的概念最早可以追述到2005年。如图,在一个图中,每个节点都是由其特征和关联节点的特征定义的。其公式描述如下:

注意,
x
n
x_n
xn 是节点
n
n
n 的状态,相当于聚合后的邻域嵌入表示,不是节点
n
n
n 的嵌入表示。GNN的目标是学习嵌入状态
x
n
∈
R
s
x_n∈R^s
xn∈Rs,该状态包含每个节点的邻域信息。状态嵌入
x
n
x_n
xn 是节点
n
n
n 的
s
s
s 维向量,可以用来产生输出
o
n
o_n
on,如节点标签。设
f
f
f 为参数函数,称为局部转移函数,该函数在所有节点之间共享,并根据输入邻域更新节点状态。
g
g
g 是局部输出函数,描述如何输出。
上式可以进一步表示为:

其中,
t
t
t 表示迭代次数。
- GNN存在一个问题就是计算效率非常低,因为要想让图中节点稳定下来,需要耗费大量的计算资源,比如对于。
- 另一个问题就是在迭代过程中,使用相同的参数,没有神经网络倡导的提取层次特征的概念。
因此,一些研究学者开始研究图的卷积操作,这可以追溯到2014年。根据欧式空间的卷积操作,尝试定义图卷积操作。
GCN
图卷积操作可以定义为:

F
F
F 表示傅里叶变换。

其中,
x
x
x 表示节点特征向量,
g
g
g 表示卷积核,
U
U
U 是归一化图拉普拉斯矩阵
L
L
L 的特征矩阵,即:
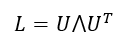
⋀
⋀
⋀ 是
L
L
L 的全部特征值组成的对角矩阵,图拉普拉斯矩阵
L
L
L 定义为:
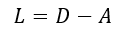


A
~
=
A
+
I
tilde{A} =A+I
A~=A+I,即添加了自连接,如果只有
A
A
A,在与特征矩阵
X
X
X 相乘时只计算了节点邻居特征之和,而忽略了自己的特征;如果
A
A
A 不经过归一化处理,与特征矩阵相乘会改变特征原本的分布。让A的每一行加起来等于1,可以乘以一个
D
D
D 的逆,即
D
(
−
1
)
A
D^{(-1) }A
D(−1)A。将
D
D
D 拆开再与
A
A
A 相乘,可以得到一个对称且归一化的矩阵。
D
~
(
−
1
/
2
)
A
~
D
~
(
−
1
/
2
)
tilde{D}^{(-1/2)}tilde{A}tilde{D}^{(-1/2)}
D~(−1/2)A~D~(−1/2) 为对称标准化拉普拉斯算子,该算子还可以被随机游走标准化拉普拉斯算子
D
~
(
−
1
)
A
tilde{D}^{(-1)} A
D~(−1)A 取代。
GraphSAGE
图卷积网络(GCN)分为两类:基于频域的GCN和基于空域的GCN。基于频域的GCN的基本思想是基于图信号处理的技术引入一种特殊的滤波器,以此来定义图卷积操作。基于空域的GCN通过信息传播来定义图卷积,从图的空间结构上进行计算。这种方式与欧式空间深度学习定义的卷积操作类似,其核心在于聚合邻居结点的信息。一种最简单的无参数的卷积方式可以是:将所有直连邻居结点的隐藏状态加和,来更新当前结点的隐藏状态。

进一步,空域卷积的形式化框架如下,它将空域卷积分解为两个过程:消息传递与状态更新操作。

后来,有研究学者提出一种归纳式图卷积方法——GraphSage。区别于传统的全图卷积,GraphSage利用采样(Sample)部分节点(保持固定的邻居)的方式进行学习。GraphSage的核心是采样和聚合。训练一组聚合函数(也就是网络参数,聚合的方式肯定是已知的),学习从节点的本地邻域聚合特征信息。假设GraphSage已经学习到了模型参数,则可以将嵌入生成描述为:



GAT
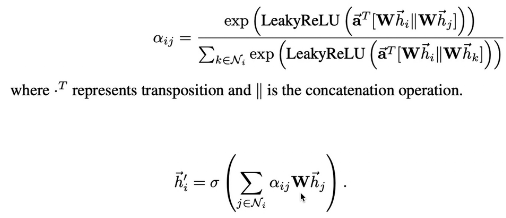
多头注意力机制:计算多次注意力机制,更好的学习两节点的相关性。


GCN(1stChebNet)、GraphSAGE和GAT对比
谱域GCN和空域GCN对比
谱域GCN
优点:
- 基于频谱的gcn有很好的理论基础,可以根据不同的信号滤波器设计不同的gcn。
缺点:
- 将整个图加载到内存中进行卷积,这对于大图形转换工作模式来说效率很低。
- 直推式工作模式
空域GCN
优点:
- 在一些技术的支持下,具有处理大图的潜力,如批处理模式训练和采样等。
- 归纳式工作模式
缺点:
- 没有严格的数学推荐
GCN和GraphSAGE对比
- GCN需要将整个图(邻接矩阵)输入进去,GraphSage不用输入整个图的拓扑结构,可以批量处理(minibatch);
- GCN是直推式的方法,GraphSage是归纳式的方法,可以处理unseen node;
- GCN聚合了每个邻居的信息,GraphSage采样固定数量的邻居;
- GCN的输入有节点编号列表、节点特征、邻接矩阵,而GraphSage的输入包括三个部分,节点编号列表、每个节点的邻居列表、节点的特征表示矩阵;
- GraphSage的损失函数鼓励邻近节点的表征相似,不连接的节点表征不同。
- GCN表面看起来是谱域方法,其实也是一种空域方法,GraphSage、GAT是空域方法;
补充
- 改变边权:GCN改变边权很简单,只需要改邻接矩阵,GraphSage改变边权或许可以参见GAT。
- 半监督任务:给定一个图,已知部分节点的label,预测图中的未知节点的label。需要已知图结构,也就是邻接矩阵。可以使用GCN、GraphSage、GAT。
- 推理学习任务:给定图的部分结构,如果一个新的节点加入,预测该节点的label;或者给定一个图,推测另一个图的节点的label。可以使用GraphSage、GAT。
最后
以上就是热情春天最近收集整理的关于Graph Neural Networks—GCN、GraphSAGE、GATGNN原始定义GCNGraphSAGEGATGCN(1stChebNet)、GraphSAGE和GAT对比的全部内容,更多相关Graph内容请搜索靠谱客的其他文章。








发表评论 取消回复