自编码器(AE)原理解析

机器学习基本分为监督学习、无监督学习、强化学习，而自编码器则是无监督学习的一种，不过它比较自觉，别人不监督它但它自己监督自己，对输入样本 $x$ 进行训练，得出结果后再与 $x$ 进行对比。

通过这一特性，自编码器可以随机生成与训练数据类似的数据，比如对图片进行重建。

AE的结构

无监督学习的数据没有额外的标注信息，只有数据 $x$ 本身。

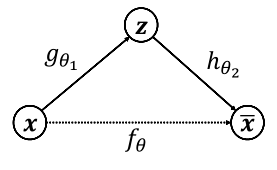
利用数据 $x$ 本身作为监督信号来指导网络的训练，即希望神经网络能够学习到映射 $f_{\theta }:x\to x$。我们把网络 $f_{\theta }$ 切分为两个部分，前面的子网络尝试学习映射关系 $g_{\theta 1}:x\to z$，后面的子网络学习映射关系 $h_{\theta 2}:z\to x$

我们把 $g_{\theta 1}$ 看成一个数据编码(Encode)过程，把高维度的输入 $x$ 编码成低维度的隐变量 $z$，称为 Encoder 网络(编码器)；把 $h_{\theta 2}$ 看成数据解码(Decode)的过程，把编码过后的的输入 $z$ 解码为搞维度的 $x$，称为 Decoder 网络(解码器)。

编码器和解码器共同完成了输入数据 $x$ 的编码和解码过程，因此整个网络 $f_{\theta }$ 自编码器(Auto-Encoder)。

运算流程

最好的状态就是解码器的输出能够完美地或者近似恢复出原来的输入，即 $\overline{x}\approx x$，因此其优化目标写为：
$$\begin{gathered} MinimizeL=dist(x,\overline{x}) \\ \overline{x}=h_{\theta 2}(g_{\theta 1}(x)) \end{gathered}$$

其中 $dist(x,\overline{x})$ 表示 $x$ 和 $\overline{x}$ 的距离度量。

AE的变种网络

为了尝试让自编码器学习到数据的真实分布，产生了一系列的自编码器变种网络。

去噪自编码器(Denoising Auto-Encoder)

给输入数据添加随机的噪声扰动，如给输入$x$ 添加采样自高斯分布的噪声 $\epsilon$：
$$\tilde{x}=x+\epsilon ,\epsilon -N(0,var)$$

添加噪声后，网络需要从 $\tilde{x}$ 学习到数据的真实隐藏变量 $z$，并还原出原始的输入 $x$，模型的优化目标：
$${\theta }^{\ast }=\underset{\theta }{\underbrace{argmin}}dist(h_{\theta 2}(g_{\theta 1}(\tilde{x})),x)$$

稀疏自编码器(Dropout Auto-Encoder)

通过随机断开网络的连接来减少网络的表达能力，防止过拟合。

根据输入数据选择性地激活网络区域，限制网络记忆输入数据的容量，而不限制网络从数据中提取特征的能力。这让我们单独考虑网络的潜在状态的表征和正则化分开，这样我们就可以根据给定数据上下文的意义选择潜在状态表征（即编码维度），同时通过稀疏性约束施加正则化。

压缩自编码器(Compression Auto-Encoder)

人们会期望对于非常相似的输入，学习的编码也会非常相似。可以为此训练模型，以便通过要求隐藏层激活的导数相对于输入而言很小。换句话说，对于输入比较小的改动，我们仍然应该保持一个非常类似的编码状态。这与降噪自编码器相似，因为输入的小扰动本质上被认为是噪声，并且希望模型对噪声具有很强的鲁棒性。

降噪自编码器使重构函数(解码器)抵抗输入有限小的扰动，而压缩自编码器使特征提取函数(编码器)抵抗输入无限小的扰动。

明确地鼓励模型学习一种编码，在这种编码中，类似的输入有类似的编码。基本上是迫使模型学习如何将输入的临近区域收缩到较小的输出临近区域。注意重构数据的斜率（即微分）对于输入数据的局部邻域来说基本为零。

可以通过构造一个损失项来实现这一点，该项对输入训练样例中的大量的衍生进行惩罚，本质上是惩罚那些在输入中有微小变化导致编码空间发生巨大变化的实例。

变分自编码器(Variational Auto-Encoder)

基本的自编码器本质上是学习输入 $x$ 和隐藏变量 $z$ 之间映射关系，它是一个判别模型，是否能将其调整为生成模型呢。

给定隐藏变量的分布 $P(z)$，如果可以学习到条件概率分布 $P(x|z)$，则通过对联合概率分布 $P(x,z)=P(x|z)P(z)$ 进行采样，生成不同的样本。

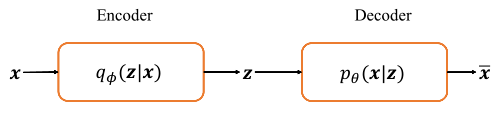
从神经网络的角度来看，VAE 相对于自编码器模型，同样具有编码器和解码器两个子网络。解码器接受输入 $x$，输出为隐变量 $z$；解码器负责将隐变量 $z$ 解码为重建的 $\overline{x}$。不同的是，VAE 模型对隐变量 $z$ 的分布有显式地约束，希望隐变量 $z$ 符合预设的先验分布 $P(z)$。因此，在损失函数的设计上，除了原有的重建误差项外，还添加了隐变量 $z$ 分布的约束项。

最后

以上就是苹果大侠为你收集整理的自编码器(AE)原理解析的全部内容，希望文章能够帮你解决自编码器(AE)原理解析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。