作者:CHEONG
公众号:AI机器学习与知识图谱
研究方向:自然语言处理与知识图谱
阅读本文之前,首先注意以下两点:
1. 机器学习系列文章常含有大量公式推导证明,为了更好理解,文章在最开始会给出本文的重要结论,方便最快速度理解本文核心。需要进一步了解推导细节可继续往后看。
2. 文中含有大量公式,若读者需要获取含公式原稿Word文档,可关注公众号【AI机器学习与知识图谱】后回复:变分推断第三讲,可添加微信号【17865190919】进学习交流群,加好友时备注来自CSDN。原创不易,转载请告知并注明出处!
本文将先对变分推断所要解决的问题进行分析,然后给出基于随机梯度上升法的变分推断解法。
一、本文结论
结论1: 变分推断的主要思想:在给定数据集 X X X下,问题是求后验概率 p p p,简单情况下后验概率 p p p可直接通过贝叶斯公式推导求出,但有些情况无法直接求解。因此变分推断想法是先假设另一个简单的概率分布 q q q,如高斯分布,通过优化 p p p和 q q q之间距离最小化,让概率分布 q q q逼近 p p p,这样就可以用概率分布 q q q近似表示后验概率 p p p。
结论2: 基于随机梯度上升法主要思路就是对优化的目标函数 q ∗ = a r g m a x q E L B O q^*=argmax_qELBO q∗=argmaxqELBO求梯度的过程。最后使用MCMC采样的方式近似求出梯度,并且考虑到求解出梯度近似值的稳定性,使用了重参数化技巧Reparameterization Trick。在梯度求出之后便可使用迭代方式求出参数。
二、问题分析
在上一节详细介绍了变分推断所要解决的问题,下面我们首先重新明确优化的目标函数
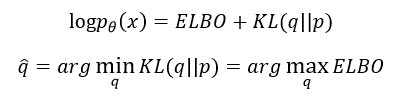
其中:
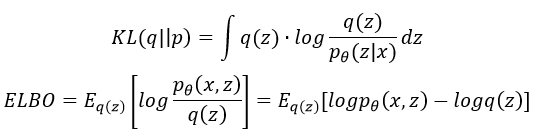
为了表示方便,这里假设 q ( z ) q(z) q(z)中 z z z是关于参数 ϕ phi ϕ的函数,这样优化函数就变成:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RYM5IxiA-1617961098543)(file:///C:/Users/zl_sd/AppData/Local/Temp/msohtmlclip1/01/clip_image024.png)]](https://www.shuijiaxian.com/files_image/2023062210/20210409174035303.png)
在明确了优化函数后,接下来就通过随机梯度上升法求解,因此下面通过公式推导求求梯度。
三、公式推导
下面是 L ( ϕ ) L(phi) L(ϕ)关于 ϕ phi ϕ求梯度的过程:
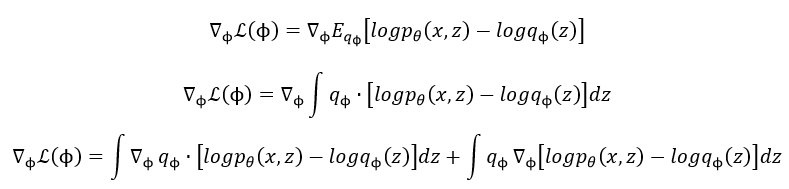
这里为了方便表示,做以下赋值操作,用 A A A表示公式前半部分,用 B B B表示公式后半部分:
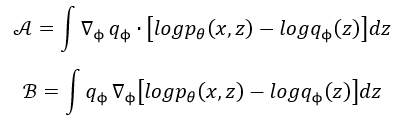
先看 B B B项,其中 l o g p θ ( x , z ) logp_theta(x,z) logpθ(x,z)与 L ( ϕ ) L(phi) L(ϕ)无关,所以有:
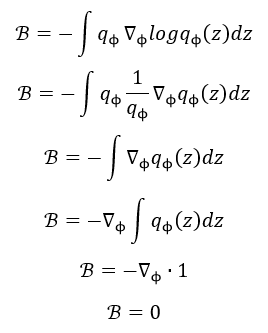
所以最终化简可得 B B B项为0,所以原始公式就只剩下 A A A项:
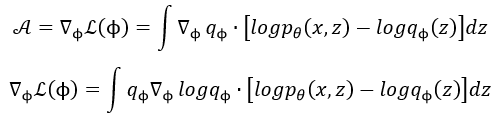
所以可以将上述式子写成 q ϕ q_phi qϕ期望的形式如下:
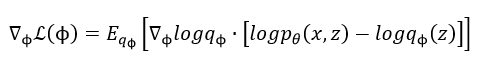
这样我们就将 L ( ϕ ) L(phi) L(ϕ)关于 ϕ phi ϕ的梯度求出来了,是一个关于 q ϕ q_phi qϕ的期望,就可以通过MCMC采样的方式把梯度具体表示出来,知道了梯度便可以利用梯度上升法进行求解了。首先通过MCMC采样法对 z z z进行采样, z l ∼ q ϕ , l = 1 , 2 , . . . , L z^l sim q_{phi}, l=1,2,...,L zl∼qϕ,l=1,2,...,L,得到 L ( ϕ ) L(phi) L(ϕ)关于 ϕ phi ϕ的梯度为:
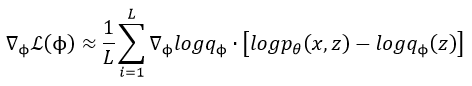
知道梯度后便可以通过随机梯度上升法求解参数:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pbvehGlq-1617961098615)(file:///C:/Users/zl_sd/AppData/Local/Temp/msohtmlclip1/01/clip_image064.png)]](https://www.shuijiaxian.com/files_image/2023062210/20210409174350533.png)
但这里存在一个问题,问题就出在:
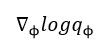
当 q ϕ q_phi qϕ很小时,如在0-1之间时,log函数的结果就会有很大的波动,会导致求出来的梯度值有很大的波动,这样MCMC采样时只有让 L L L取非常大时才能避免这种波动带来的高方差High Variance的问题,所以在实际使用时存在工程上的问题。解决的方案就是使用重参数化技巧来避免。
四、重参数化技巧
Reparameterization Trick,假设:
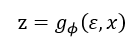
其中
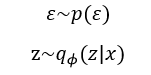
则:
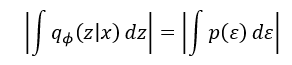
在使用重参数化技巧之后,我们再来求目标函数的梯度值:
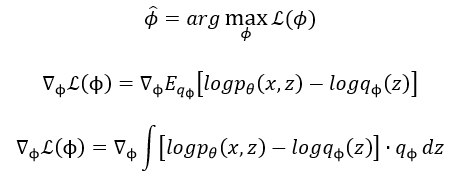
这里将 q ϕ q_phi qϕ可以利用重参数化技巧可以等价替换成 p ( ε ) p(varepsilon) p(ε):
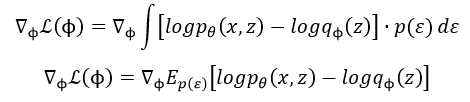
这里就是关于 p ( ε ) p(varepsilon) p(ε)的期望了,所以对 ϕ phi ϕ求梯度时就不会那么复杂
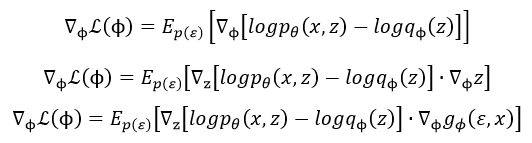
这里我们再使用MCMC采样法对 ε varepsilon ε进行采样, ε l ∼ p ( ε ) , l = 1 , 2 , . . . , L varepsilon^l sim p(varepsilon), l=1,2,...,L εl∼p(ε),l=1,2,...,L,最终可以得出目标函数的梯度值为:
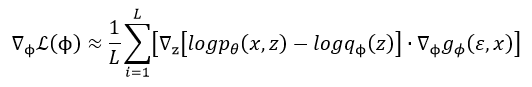
得知梯度值之后,便可以使用随机梯度上升法对参数进行迭代求解:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aMNGRNor-1617961098694)(file:///C:/Users/zl_sd/AppData/Local/Temp/msohtmlclip1/01/clip_image064.png)]](https://www.shuijiaxian.com/files_image/2023062210/20210409174543591.png)
最后
以上就是大力小兔子最近收集整理的关于【机器学习系列】变分推断第三讲:基于随机梯度上升法SGD的变分推断解法一、本文结论二、问题分析三、公式推导四、重参数化技巧的全部内容,更多相关【机器学习系列】变分推断第三讲:基于随机梯度上升法SGD内容请搜索靠谱客的其他文章。








发表评论 取消回复