题目描述

给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

算法思路

二叉树天然适合递归。

第一版：

class Solution:
    def trimBST(self, root: TreeNode, L: int, R: int) -> TreeNode:
        if root==None:return None
        # if root.val<L:root=root.right
        # elif root.val>R:root=root.left
        # if root==None:return None
        # root.left=self.trimBST(root.left,L,R)
        # root.right=self.trimBST(root.right,L,R)
        # return root

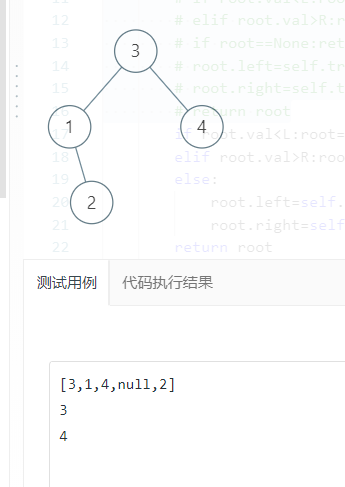
输出结果是[3,2,4]，答案是[3,null,4]。
很显然，在节点1这里，root=root.right，然后节点2没有得到验证直接进行

# root.left=self.trimBST(root.left,L,R)
# root.right=self.trimBST(root.right,L,R)

然后返回了。

简单思考后：
第二版：

class Solution:
    def trimBST(self, root: TreeNode, L: int, R: int) -> TreeNode:
        if root==None:return None
        if root.val<L:root=self.trimBST(root.right,L,R)
        elif root.val>R:root=self.trimBST(root.left,L,R)
        else:
            root.left=self.trimBST(root.left,L,R)
            root.right=self.trimBST(root.right,L,R)
        return root

执行用时 :52 ms, 在所有 Python3 提交中击败了85.43%的用户

最后

以上就是乐观黑裤为你收集整理的【力扣日记】669 修剪二叉搜索树 | 递归题目描述算法思路的全部内容，希望文章能够帮你解决【力扣日记】669 修剪二叉搜索树 | 递归题目描述算法思路所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。