二叉树的路径总和

一、题目

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

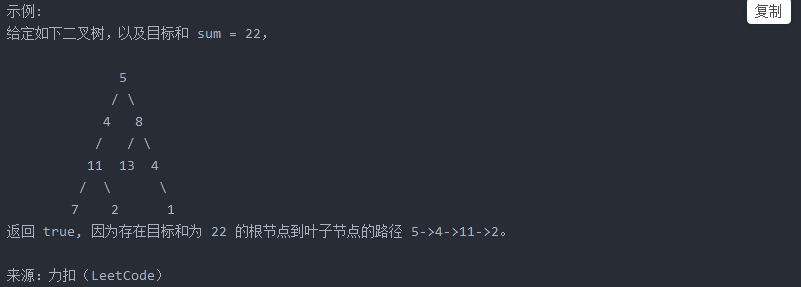
二、解析

1、最直接的方法就是利用递归，遍历整棵树：如果当前节点不是叶子，对它的所有孩子节点，递归调用 hasPathSum 函数，其中 sum 值减去当前节点的权值；如果当前节点是叶子，检查 sum 值是否为 0，也就是是否找到了给定的目标和。

class Solution {
public:
	bool hasPathSum(TreeNode* root, int sum) {
		if (root == nullptr)
			return false;

		sum -= root->val;
		if ((root->left == nullptr) && (root->right == nullptr))
			return (sum == 0);
		return hasPathSum(root->left, sum) || hasPathSum(root->right, sum);
	};
};

复杂度分析

    时间复杂度：我们访问每个节点一次，时间复杂度为 O(N) ，其中N 是节点个数。
    空间复杂度：最坏情况下，整棵树是非平衡的，例如每个节点都只有一个孩子，递归会调用 NNN 次（树的高度），因此栈的空间开销是 O(N) 。但在最好情况下，树是完全平衡的，高度只有 log⁡(N)，因此在这种情况下空间复杂度只有 O(log⁡(N)) 。

2、迭代法。使用两个栈，一个栈保存节点，一个栈保存遍历过的节点的总和，若遍历到叶子节点且该节点的栈的值是sum值就返回true

class Solution {
public:
    //非递归模式，使用两个栈，一个栈保存节点一个栈保存遍历过的节点的总和
    bool hasPathSum(TreeNode* root, int sum) {
        if(!root) return false;
        stack<TreeNode*> path;
        stack<int> sub;
        path.push(root);
        sub.push(root->val);
        while(!path.empty()){
            TreeNode* pnode = path.top();
            path.pop();
            int pval = sub.top();
            sub.pop();
            if(!pnode->left && !pnode->right && pval==sum) return true;
           
            if(pnode->left){
                path.push(pnode->left);
                sub.push(pval+pnode->left->val);
            }
            if(pnode->right){
                path.push(pnode->right);
                sub.push(pval+pnode->right->val);                          
            }
        }
        return false;
    }
};
。

复杂度分析

    时间复杂度：和递归方法相同是 O(N)O(N)O(N)。
    空间复杂度：当树不平衡的最坏情况下是 O(N)O(N)O(N) 。在最好情况（树是平衡的）下是 O(log⁡N)O(log N)O(logN)

参考：

https://blog.csdn.net/qq_37465638/article/details/103352167

最后

以上就是帅气丝袜为你收集整理的二叉树的路径总和的全部内容，希望文章能够帮你解决二叉树的路径总和所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。