概述
向量范数和矩阵范数
研究意义：为了研究解的误差分析和迭代法的收敛性
什么是向量范数？
说到底，向量范数就是一种函数f(x)，目的就是把一个向量和一个数值进行映射
由于平时你根本不会用这些东西来进行设计，所以下面给出
几个经典的向量范数的例子。
向量的1范数：向量的各个元素的绝对值之和
向量的2范数即：向量的每个元素的平方和再开平方根（像不像柯西不等式？）
向量的正无穷范数即：向量的所有元素的绝对值中最大的。
如果你学过数学竞赛，你应该反应过来了：这不就是柯西不等式的高次扩展吗?
矩阵范数
这里只比向量范数
几个经典的矩阵范数的例子。
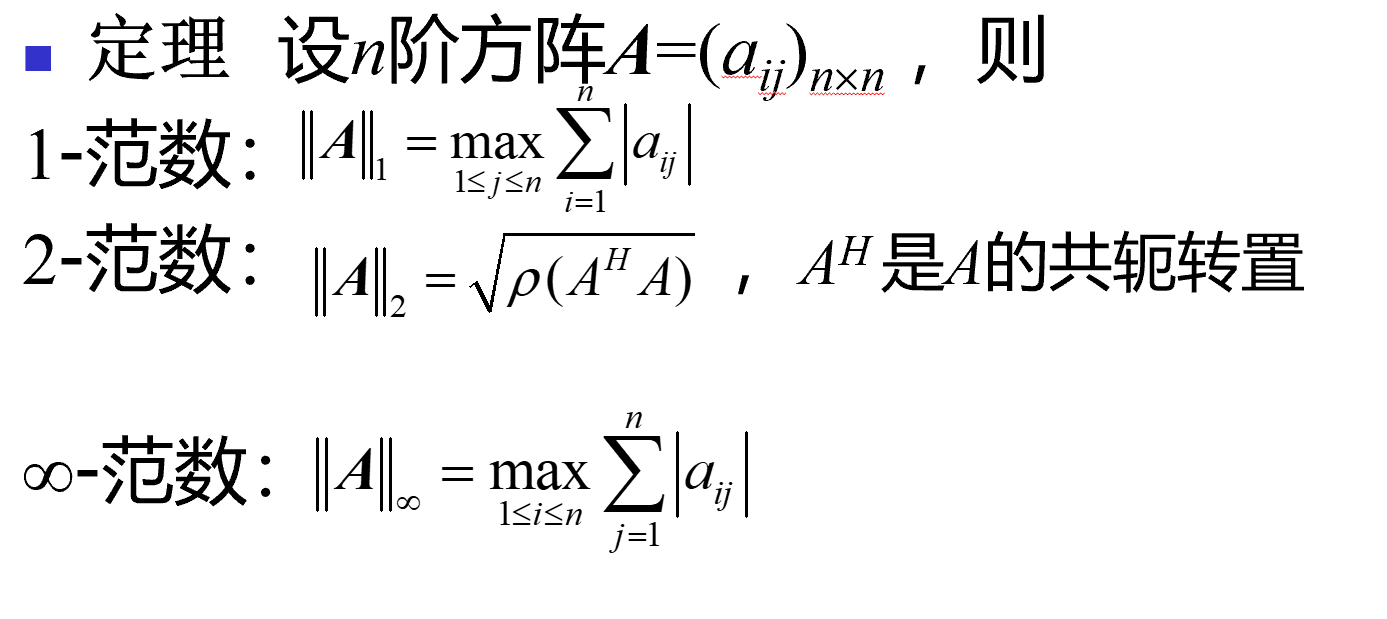矩阵的1范数就是每一列元素之和的最大值
矩阵的∞范数就是每一行元素之和的最大值
至于为什么是这样其实比较复杂
因为任何一个矩阵范数的得到都是可以通过向量范数产生的从属范数而定义的。
也就是说，得到一个一个矩阵范数有两种途径：
1.依据定义直接凭空构造
2.通过向量范数构造
然后你把两种都构造出来，发现两者是一模一样的，那你肯定选向量范数构造啊（毕竟简单啊）
最后
以上就是呆萌帆布鞋为你收集整理的向量范数和矩阵范数（理论推导+快速记忆1、2、∞范数）向量范数和矩阵范数的全部内容，希望文章能够帮你解决向量范数和矩阵范数（理论推导+快速记忆1、2、∞范数）向量范数和矩阵范数所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复