栈是一种操作受限的线性表,只允许在一端插入和删除数据。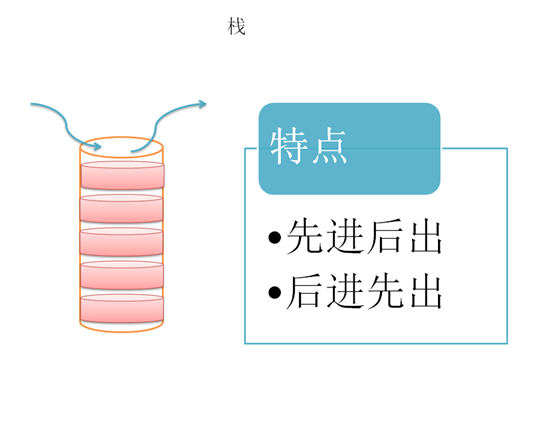
栈的实现:
栈,即可以用数组来实现,也可以用链表来实现,使用数组来实现的栈叫顺序栈,使用链表来实现的栈叫链式栈。
这是基于java语言来分别实现的顺序栈和链式栈.
顺序栈
/** * 用数组实现一个顺序栈 * * <p>栈,先进后出,后进的先出 * * @author liujun * @version 0.0.1 * @date 2019/08/07 */ public class MyArrayStack { private final int[] stackArray; /** 限制栈的大小 */ private final int maxStackSize; /** 当前栈的大小 */ private int currSize = -1; /** * 进行栈的初始化操作 * * @param stackSize */ public MyArrayStack(int stackSize) { this.maxStackSize = stackSize; this.stackArray = new int[stackSize]; } /** * 栈中放入一个数 * * @param value */ public void push(int value) { if (currSize + 1 > maxStackSize) { throw new IndexOutOfBoundsException("index out of bounds "); } stackArray[++currSize] = value; } /** * 获取当前栈的大小 * * @return */ public int size() { return currSize + 1; } /** * 从栈中取出一个元素 * * @return 取出的栈顶的元素 */ public int pop() { if (currSize < 0) { throw new NegativeArraySizeException("index is less than 0 "); } int getValue = stackArray[currSize]; stackArray[currSize] = -1; currSize--; return getValue; } } |
链式栈
/** * 使用链表实现链式栈 * * @author liujun * @version 0.0.1 * @date 2019/08/14 */ public class MyLinkedStack { class Node { private int val; private Node next; public Node(int val) { this.val = val; } } private Node root = new Node(-1); /** 最大的链式栈大小 */ private final int maxSize; /** 当前大小 */ private int size; public MyLinkedStack(int maxSize) { this.maxSize = maxSize; this.size = 0; } /** * 插入数据到栈顶 * * @param value */ public void push(int value) { if (size > maxSize) { throw new IndexOutOfBoundsException("exceed the limit"); } // 1,获得原来链表的下级节点 Node nextTmp = root.next; Node currTmpNode = new Node(value); root.next = currTmpNode; currTmpNode.next = nextTmp; size++; } public boolean full() { return size == maxSize; } // 获取当前链式栈的大小 public int size() { return size; } /** * 实现弹出栈顶操作 * * @return */ public int pop() { if (size < 1) { throw new NullPointerException("stack is null"); } // 1,找到栈顶元素 Node tmpNode = root.next; if (tmpNode == null) { return -1; } // 找到下级元素 Node nextValue = null; nextValue = tmpNode.next; int value = tmpNode.val; root.next = nextValue; size--; return value; } } |
栈的应用:
括号的有效性判断:
leetcode题目:
Given a string containing just the characters '(', ')', '{', '}', '[' and ']',
determine if the input string is valid.
An input string is valid if:
Open brackets must be closed by the same type of brackets.
Open brackets must be closed in the correct order.
Note that an empty string is also considered valid.
Example 1:
Input: "()"
Output: true
Example 2:
Input: "()[]{}"
Output: true
Example 3:
Input: "(]"
Output: false
Example 4:
Input: "([)]"
Output: false
Example 5:
Input: "{[]}"
Output: true
检查括号输入括号是否有效,包括”{”, ”}” , ”[” , ”]” , ”(” , ”)”,检查需要支持括号嵌套。
我的代码实现
/** * 解决方案 * * <p>通过定义枚举进行括号的配对操作 * * @author liujun * @version 0.0.1 * @date 2018/11/17 */ public class Solution { public enum BracketEnum { /** 小括号 */ PARENTHESES('(', ')'), /** 中括号 */ BRACKETS('[', ']'), /** 大括号 */ CURLYBRACES('{', '}'); private char left; private char right; BracketEnum(char left, char right) { this.left = left; this.right = right; } public static boolean left(char val) { for (BracketEnum item : values()) { if (item.left == val) { return true; } } return false; } public static BracketEnum right(char val) { for (BracketEnum item : values()) { if (item.right == val) { return item; } } return null; } } public boolean isValid(String s) { if (null == s) { return false; } if (s.length() == 0) { return true; } char[] braket = s.toCharArray(); Stack<Character> leftStack = new Stack(); BracketEnum bracket = null; for (int i = 0; i < braket.length; i++) { // 如果为左括号压入左括号左括号栈中 if (BracketEnum.left(braket[i])) { leftStack.push(braket[i]); } else { // 如果为右括号,则从左侧栈中弹出一个做比较,一至则不放入 if ((bracket = BracketEnum.right(braket[i])) != null) { if (!leftStack.isEmpty()) { char left = leftStack.pop(); if (left != bracket.left) { return false; } } else { return false; } } } } return leftStack.isEmpty(); } } |
进行分解成示意图就是图中这个操作流程.
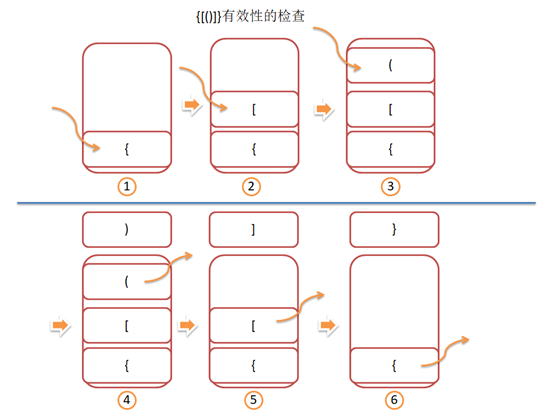
这样看起来非常的简单,在遇到左括号时,进行压栈操作,在遇到右括号时进行出栈操作。
当发生一个括号不能匹配时,则可以直接返回校验失败,当所有的括号都遍历完成后,如果栈为空,说明匹配成功,否则匹配失败。接下来详细说明下整个过程以”{[()]}”为例
- 在遇到”{”括号了,进行压栈操作。就像1中所示.
- 接下来是”[”括号,也是左括号,进行压栈操作。如2所示
- 在接下来遍历的是”(”,同样是左括号,也同样进行压栈操作。如3
- 接下来遇到的是”)”,此时是右括号,将从栈顶元素同当前括号进行配对,“()”正好配对成功,将”(”出栈。如4
- 再接下来是”]”,此时也是右括号,将同栈顶元素进行配对操作。“[]”也可以匹配成功。将”[”出栈。如5
- 再接下来就是最后一个字符”}”,与栈顶元素”{”,可以配对成功,将”{”出栈。如6所示。
当遍历完成后,栈已经为空,说明配对成功。
针对这个来说,还有更优的解法。此参考了leetcode上其他人的实现。
/** * 解决办法 * * <p>使用数组来实现栈的功能 * * @author liujun * @version 0.0.1 * @date 2018/11/17 */ public class SolutionArrayStackOther { public boolean isValid(String s) { if (null == s) { return false; } if (s.length() == 0) { return true; } char[] stack = new char[s.length()]; int stackIndex = -1; char data; int readIndex = 0; while (readIndex < s.length()) { data = s.charAt(readIndex); if (data == ' ') { readIndex++; continue; } if (data == '(' || data == '{' || data == '[') { stack[++stackIndex] = data; } else if (data == ')' || data == '}' || data == ']') { if (stackIndex >= 0 && ((stack[stackIndex] == '(' && data == ')') || (stack[stackIndex] == '{' && data == '}') || (stack[stackIndex] == '[' && data == ']'))) { stackIndex--; } else { return false; } } readIndex++; } return stackIndex == -1; } } |
表达式的求值:
Leetcode227:
227 basic calculator 2
Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, +, -, *, / operators and empty spaces .
The integer division should truncate toward zero.
Example 1:
Input: "3+2*2"
Output: 7
Example 2:
Input: " 3/2 "
Output: 1
Example 3:
Input: " 3+5 / 2 "
Output: 5
Note:
You may assume that the given expression is always valid.
Do not use the eval built-in library function.
注:需要注意的是在乘除法的优先级比加减法要高,需要进行优先计算。
可以通过两个栈来实现一个保存数值的栈,一个保存操作数的栈。当遇到操作数时就进行压栈操作,
当遇到操作符时,就与栈顶元素作比较,如果比栈顶元素的优先级高。就将当前操作符压栈操作;如果比栈顶元素的优先级低,则弹出两个操作数与一个操作符进行运算。然后继续比较。
我的实现:
/** * 一个简单的非负数的计算器的实现 * * @author liujun * @version 0.0.1 * @date 2019/08/16 */ public class SolutionCalculator { enum OperEnum { PLUS('+', 1), MINU('-', 1), MULT('*', 2), DIVI('/', 2), ; private char oper; private int order; public static OperEnum getOper(char item) { OperEnum oper = null; for (OperEnum operitem : values()) { if (operitem.oper == item) { oper = operitem; } } return oper; } OperEnum(char oper, int order) { this.oper = oper; this.order = order; } } public int calculate(String s) { if (s == null || s.isEmpty()) { return 0; } // 数值栈 Stack<Integer> valueStack = new Stack<>(); // 操作数栈 Stack<Character> operStack = new Stack<>(); int curIndex = 0; char charItem; while (curIndex < s.length()) { charItem = s.charAt(curIndex); if (charItem >= '0' && charItem <= '9') { int currValue = 0; //进行数字的提取,比较巧妙。利用的是位之前是10的倍数的关系,然后再加当前数。 while (curIndex < s.length() && Character.isDigit(s.charAt(curIndex))) { currValue = currValue * 10 + (s.charAt(curIndex) - '0'); curIndex++; } // 将操作数压栈操作 valueStack.push(currValue); continue; } else if (charItem == OperEnum.PLUS.oper || charItem == OperEnum.MINU.oper || charItem == OperEnum.MULT.oper || charItem == OperEnum.DIVI.oper) { if (operStack.isEmpty()) { operStack.push(charItem); } else { OperEnum operLast = OperEnum.getOper(operStack.peek()); OperEnum operCurr = OperEnum.getOper(charItem); //算法符的优先级比较 if (operCurr.order > operLast.order) { operStack.push(charItem); } else { // 执行运算 runCount(valueStack, operStack, operCurr); operStack.push(charItem); } } } curIndex++; } if (!operStack.isEmpty()) { runCount(valueStack, operStack, null); } return valueStack.pop(); } /** * 进行栈中数据的计算操作 * @param valueStack 数据栈 * @param operStack 操作符栈 * @param operCurr 当前操作符 */ private void runCount(Stack<Integer> valueStack, Stack<Character> operStack, OperEnum operCurr) { while (!operStack.isEmpty()) { //栈中的操作符优先级低于当前操作符优先级,则不运算。 OperEnum lastStack = OperEnum.getOper(operStack.peek()); if (null != operCurr && lastStack.order < operCurr.order) { break; } char currValue = operStack.pop(); int value2 = valueStack.pop(); int value1 = valueStack.pop(); if (currValue == OperEnum.PLUS.oper) { valueStack.push(value1 + value2); } else if (currValue == OperEnum.MINU.oper) { valueStack.push(value1 - value2); } else if (currValue == OperEnum.MULT.oper) { valueStack.push(value1 * value2); } else if (currValue == OperEnum.DIVI.oper) { valueStack.push(value1 / value2); } } } } |
详细的运算流程:
以3+2*2/2+6为例
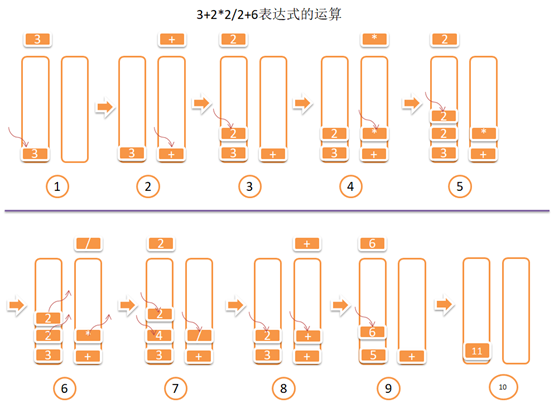
- 解析到数字将数字3,压入到数值栈中。
- 解析到操作符+,此时操作符栈为空,将当前操作符+直接压入到操作符栈中。
- 解析到数字2,将2压入到数值栈中。
- 解析到操作符*号,由于乘法的优先级高于加法,因此,将操作符*压入栈中。
- 解析到数字2,将2压入到数值栈中
- 解析到数字/号,由于除号的优先级与乘法相同,因此将弹出两个操作数“2”,“2”及一个操作符*号进行运算得到4,将结果4压入到数值栈中,再将/号压入到操作符栈中。
- 解析到2,将2压入到数值的栈中
- 解析到+号,由于+号的优先级低于除法的优先级,因此将弹出两个操作数“4”,“2”及操作符/号,进行运算得到2,将结果2,压入到数值栈中,当前操作符+号与操作符栈中的+号优先级相同,所以会再次弹出两个操作数“3”,“2”和一个操作符“+”进行运算得到5,将5压入到数值栈中。再将当前+号压入到操作数栈中。
- 解析到6,将6压入到数值栈中。当前遍历结束。
- 当前操作符栈中还存在操作符,将弹出两个数值“5”,“6”和一个操作符+,进行运算处到11
这就是一个数值表达式计算的完整的过程。
最后
以上就是留胡子汉堡最近收集整理的关于栈的全部内容,更多相关栈内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复