obsidian技巧

1、引用

Human beings face ever more complex and urgent problems, and their effectiveness in dealing with these problems is a matter that is critical to the stability and continued progress of society.

2、代码块

如果使用Tab键对段落进行缩进，这段文本在预览模式下也会被识别为代码块。

如果使用Tab键对段落进行缩进，这段文本在预览模式下也会被识别为代码块。	

3、行内代码

一行中被 反引号 括起来的文字会以代码格式显示。

4、数学公式

行内公式用单$

• 简单语法：$E=mc^2$$E=m{c}^2$
• LaTex语法：$$begin{bmatrix}x\yend{bmatrix}$$
  $$\left[\begin{array}{c}x\\ y\end{array}\right]$$
  可使用公式编辑器：在线LaTeX公式编辑器

公式换行

在以

begin{aligned}
……
end{aligned}

begin{split}
……
end{split}

为首尾的公式内，以\表换行，以&表对齐，如：

$$begin{aligned}
KPI&=(N+S)W \
PI&=N+S \
I&=W
end{aligned}$$

$$\begin{array}{rl}KPI& =(N+S)W\\ PI& =N+S\\ I& =W\end{array}$$

$$begin{split} 
loss&=(y_i-Q(s,a;theta))^2 \
&=(r+gamma max Q(s^{'},a^{'};theta^{-})-Q(s,a;theta)) ^2\
end{split}$$

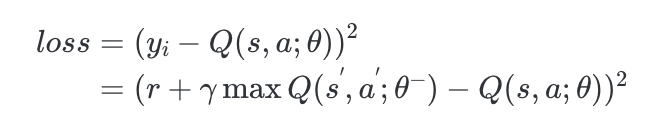
$$begin{aligned} 
抽样定理:&一个频带限制在(0，f_{H})内的连续时间信号m(t)，\
&如果以Ts≤1/(2f_{H})的间隔对其进行等间隔抽样，\
&则m(t)将被这些抽样值完全确定。也就是说，\
&如果以fs≥2f_{H}的抽样频率进行均匀抽样，\
&m(t)可以被得到的抽样值完全确定。\
&最小抽样频率fs=2f_{H}称为奈奎斯特频率，\
&最大抽样间隔Ts=1/(2f_{H})称为奈奎斯特间隔。
end{aligned}$$

$$\begin{array}{rl}抽样定理:& 一个频带限制在(0，f_H)内的连续时间信号m(t)，\\ & 如果以Ts\le 1/(2f_H)的间隔对其进行等间隔抽样，\\ & 则m(t)将被这些抽样值完全确定。也就是说，\\ & 如果以fs\ge 2f_H的抽样频率进行均匀抽样，\\ & m(t)可以被得到的抽样值完全确定。\\ & 最小抽样频率fs=2f_H称为奈奎斯特频率，\\ & 最大抽样间隔Ts=1/(2f_H)称为奈奎斯特间隔。\end{array}$$

5、外部链接

外部链接:[百度](https://www.baidu.com)
百度

6、内部链接

1. 普通内部链接:[[线性代数]]
   [[线性代数]]
2. |更改显示的文本:[[线性代数|线代]]
   [[线性代数|线代]]
3. /路径索引，防重名:[[自然科学/数学/线性代数]]
   [[自然科学/数学/线性代数]]
4. #链接到标题:[[线性代数#矩阵（Matrix）]]
   [[线性代数#矩阵（Matrix）]]
5. ^链接到文本块，并更改显示的文本:[[线性代数#^8b822a|线性代数定义]]
   [[线性代数#^8b822a|线性代数定义]]
6. 链接并预览:![[线性代数]]
   ![[线性代数]]

最后

以上就是潇洒白云为你收集整理的obsidian技巧的全部内容，希望文章能够帮你解决obsidian技巧所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。