神经网络

     简单介绍一下什么是神经网络，以及其原理

感知器(Perceptrons)

如图所示 ：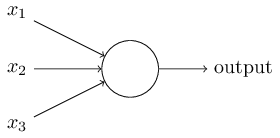

        这个感知器有3个input和一个output，分别是$x_1,x_2,x_3$，有一个output。一个感知器可以拥有多个input，如$x_1,x_2, ldots$。 input和output的值都有一个特点，就是只能是1或者0，也就是说$x_1,x_2, ldots$只能取0或者1，而output也只能取0或者1.那么如何决定到底输出0还是1呢？就根据每个input的权重(weight)，把每个权重和input的值相乘，结果相加($sum_j w_j x_j$ )，再和某个阈值进行比较，如果结果比某个阈值大，那么就输出1，比阈值小，就输出0。数学公式为:

$$begin{eqnarray} mbox{output} & = & left{ begin{array}{ll} 0 & mbox{if } sum_j w_j x_j leq mbox{ threshold} \ 1 & mbox{if } sum_j w_j x_j > mbox{ threshold} end{array} right. tag{1}end{eqnarray}$$ 这个模型基本上可以看做是一个逻辑电路，只不过多了权重和阈值。

如图所示：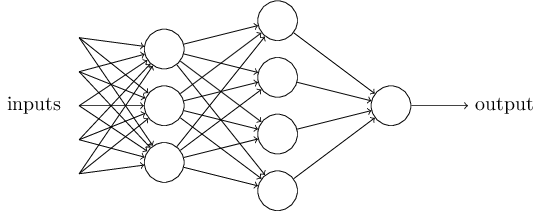

       左边的第一列被称为感知器的第一层，有三个input，可以做三个简单的决定，那么为什么还需要中间的第二层呢？是因为第二层可以另整个感知器做更多的更抽象的选择。而第三层只有一个感知器(perceptron)，但实际上可以有更多个。公式$sum_j w_j x_j >mbox{ threhold}$

可以进行变形，另 $b equiv -mbox{threshold}$，而 $sum_j w_j x_j$写成点积的形式，即为： $$begin{eqnarray} mbox{output} = left{ begin{array}{ll} 0 & mbox{if } wcdot x + b leq 0 \ 1 & mbox{if } wcdot x + b > 0 end{array} right. tag{2}end{eqnarray}$$

sigmoid神经元(Sigmoid neurons)

       假设我们有了一个感知器组成的神经网络，开始进行深度学习，我们想要识别手写的阿拉伯数字，输入的是以每个像素值为最小单位的矩阵，而输出的是识别的结果。如果网络最后将8识别成了9，我们想要去纠正它，只要我们更改一点input的权重和阈值，而整个网络输出的结果也只改变一点的话，我们就可以每次改变微笑的量，直到网络输出正确的结果为止。但实际上，如果我们改变一点权重或者阈值，整个网络的输出结果可能会有翻天覆地的变化，这就使得学习算法非常难以应用了。因此，我们引入一个新的类型的人工智能神经元:sigmoid neuronsigmoid neuron。这种神经元和感知器有相似的地方，但是不同的地方是：input中一些微小的权重和阈值的变化，只会引起output微小的变化。sigmoid neuron如图所示：

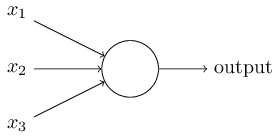
和感知器一样，有input，output，不同的地方是，不在像感知器一样输出$0$和$1$了，而是输出一个函数:

$$begin{eqnarray} sigma(z) equiv frac{1}{1+e^{-z}}. tag{3}end{eqnarray}$$ ,其中，因为inputs是 $x_1,x_2,ldots$, weights $w_1,w_2,ldots$, and bias $b$ ，所以3式又可以换成：

$$begin{eqnarray} frac{1}{1+exp(-sum_j w_j x_j-b)}. tag{4}end{eqnarray}$$

我们来分析一下方程(4)：我们假设$z equiv w cdot x + b$ ，也就是sigmoid neuron的input是一个非常大的数，那么 $e^{-z}$的结果就无限接近于0，则σ(z)的值就非常接近于1，而当z为一个非常小的负数，则σ(z)的结果无限接近于1.也就是说σ(z)的值域在(0,1)区间。因为 $sigma$ 是连续函数，所以，$Delta w_j$和 $Delta b$ 的微小变化，会让$Delta mbox{output}$ 也产生微小变化，这样就令训练成为了可能。根据微积分，

$$begin{eqnarray} Delta mbox{output} approx sum_j frac{partial , mbox{output}}{partial w_j} Delta w_j + frac{partial , mbox{output}}{partial b} Delta b, tag{5}end{eqnarray}$$

$Delta {partial w_j}$为函数$sigma(z)$对w的偏导，$Delta{partial b_j}$为函数$sigma(z)$对变量b的偏导。

神经网络的结构

        先介绍一些术语，如下图所示：

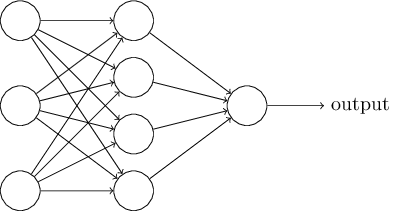
最左边的一列叫做输入层(input layer)，而中间的一列叫做隐蔽层(hidden layer)，最右边的一列叫做输出层(output layer)。在输入层的神经元被称为输入神经元(input neurons)，而在输出层的神经元被称为输出神经元(output neurons)

输入层和输出层可以有多个神经元，而且隐蔽层可以有很多层。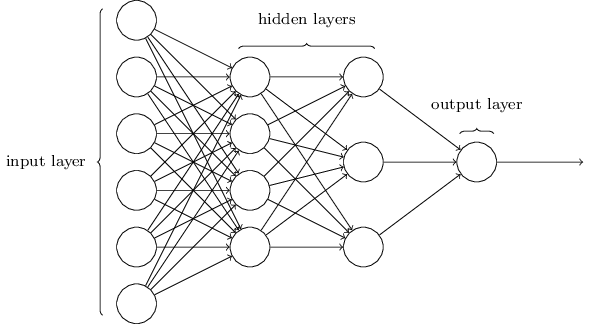

       如图就是一个拥有两层隐蔽层的神经网络。因为历史原因，有时候图中的神经网络会被叫做多层感知器，虽然和感知器没有关系。

        想要几个简单的规则就能设计出隐蔽层是不可能的

        目前为止，我们谈论的神经网络都不存在循环，即信息总是向前传输。但是，的确有些神经网络存在循环，我们称这些网络为循环神经网络

参考资料： 《Neural Networks and DeepLearning》 Michael Nielsen

最后

以上就是年轻期待为你收集整理的神经网络简介神经网络的全部内容，希望文章能够帮你解决神经网络简介神经网络所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。