九小时九个人九扇门（01背包变形）- 牛客

原题链接

题面

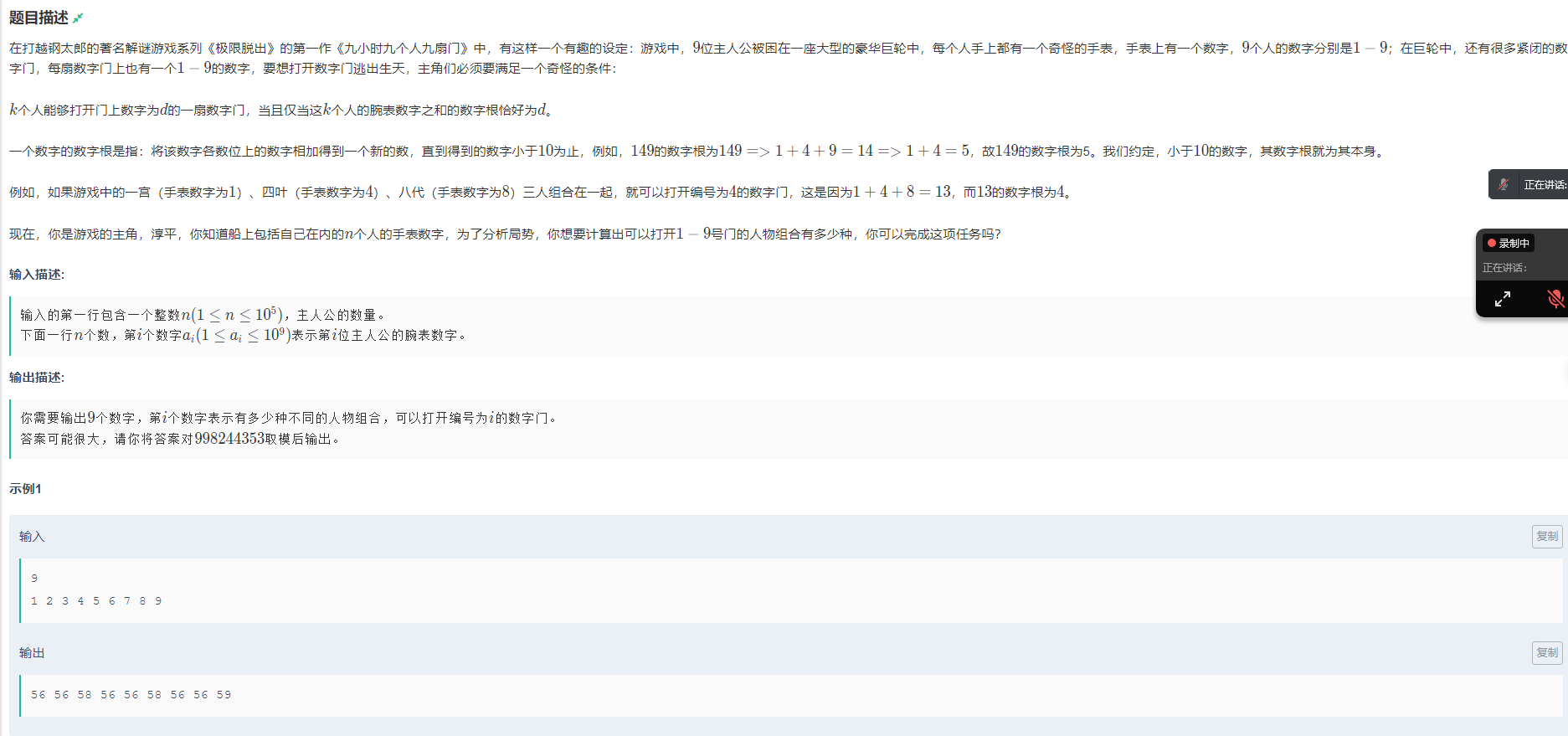
思路

• 很容易发现，几个数字的数字根就是这几个数字相加的和 $mod9$，然后中间某些数 $mod9$ 也不会影响结果，有点像结合律。
• 那么这道题就可以转换为一个01背包。
• 定义 $f_{ij}$ 为 选前i种，当前和 j 加时的总方案数
• 为了方便转移，初始化 $f_{00}$ 为 $1$
• $f_{ij}+=f_{(i-1)j}$，这是不选当前这件物品时的方案数
• $f_{i((j+x)mod9)}+=f_{(i-1)j}$，因为加上这件物品后的数量就建立在这个当前这个j上，j通过j加上这个数能组成新数的方案就等于所有能组成j的方案，那么多方案都加上当前数结果是一样的。
• 计算时注意取模
• 最后输出答案时，把取模结果为0的数作为9的方案数输出
• 还要把0的方案-1，因为那个初始化。

代码

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N = 1e5 + 10, mod = 998244353;
int a[N];
int f[N][10];
int sum[N];
signed main()
{
	int n; cin >> n;
	for (int i = 1; i <= n; i ++ )
	{
		cin >> a[i];
		a[i] %= 9;
	}
	f[0][0] = 1;
	for (int i = 1; i <= n; i ++ )
	{
		for (int j = 0; j < 9; j ++ )
		{
			f[i][(j + a[i]) % 9] = (f[i][(j + a[i]) % 9] + f[i - 1][j]) % mod;
			f[i][j] += (f[i - 1][j] % mod);
			f[i][j] %= mod;
		}
	}
	for (int i = 1; i < 9; i ++ )
	{
		cout << f[n][i] << " ";
	}
	cout << f[n][0] - 1;
	return 0;
}

总结

01背包变形。

最后

以上就是淡然春天为你收集整理的九小时九个人九扇门（01背包变形）- 牛客的全部内容，希望文章能够帮你解决九小时九个人九扇门（01背包变形）- 牛客所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。