概述
文章目录
- A. Casimir's String Solitaire
- B. Shifting Sort
- C. Ticks
- D - Productive Meeting
- E1. Permutation Minimization by Deque
- E2. Array Optimization by Deque
- F. Array Stabilization (AND version)
- G. Minimal Coverage
A. Casimir’s String Solitaire
题意：
对于一个字符串，有两种操作:
1、选择字符串中的一对‘A’和‘B’，删除他们；
2、选择字符串中的一对‘B’和‘C’，删除他们；
问能否通过一系列操作把字符串变成空串。
思路：
计三种字符的个数，只要’B’的个数是’A’和‘C’的个数和即可。
代码：
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main(){
int t;
cin>>t;
while(t--){
string s;
cin>>s;
int cnt1=0,cnt2=0,cnt3=0;
for(int i=0;i<s.length();i++){
if(s[i]=='A')cnt1++;
else if(s[i]=='B')cnt2++;
else cnt3++;
}
if(cnt2==cnt1+cnt3)cout<<"YESn";
else cout<<"NOn";
}
return 0;
}
B. Shifting Sort
题意：
给你一个长度为
n
,
n
<
=
50
n,n<=50
n,n<=50的序列，每次可以选择一个区间，循环向左位移几位，即区间头部几位移到区间末尾，其他树向前补上空格；
用
x
<
=
n
x<=n
x<=n次操作使序列变成升序，输出操作序列。
思路：
用结构体存储操作序列，如果有的数已经在位置上了就不操作。因为
n
<
=
50
n<=50
n<=50直接暴力枚举即可。
代码：
#include<bits/stdc++.h>
using namespace std;
#define ll long long
struct node{
int l,r,d;
}z[100];
int cnt=0;
int s[100];
int a[100];
int main(){
int t;
cin>>t;
while(t--){
cnt=0;
int n;
cin>>n;
for(int i=1;i<=n;i++)cin>>s[i];
for(int i=1;i<=n;i++){
int pos=i;
for(int j=i+1;j<=n;j++){
if(s[j]<s[pos])pos=j;
}
if(pos==i)continue;
cnt++;
z[cnt].l=i;z[cnt].r=n;
z[cnt].d=pos-i;
for(int j=i;j<pos;j++){
a[j-i+1]=s[j];
}
for(int j=pos;j<=n;j++){
s[j-z[cnt].d]=s[j];
}
for(int j=n-z[cnt].d+1;j<=n;j++){
s[j]=a[j-n+z[cnt].d];
}
}
cout<<cnt<<endl;
for(int i=1;i<=cnt;i++){
cout<<z[i].l<<" "<<z[i].r<<" "<<z[i].d<<endl;
}
}
return 0;
}
C. Ticks
题意：
给你一个
n
∗
m
n*m
n∗m的网格，每次可以在网格上涂一个形如‘V’字形的图形，一个V形图案的大小定义为V字边的长度。
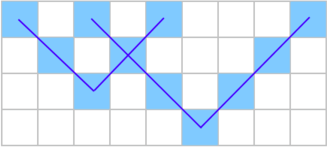
如图左边的V大小为2，右边的大小为3。
初始图为空白的，判断是否能通过在图上画几个大小 大于给定值的V形，让图变成给定图。
思路：
同样数据范围很小，可以暴力一点。
直接枚举每个星号做为V的下部顶点的情况，如果V的大小大于给定值，就把这些星号做个标记。
最后检查是否所有的星号都做了标记。
代码：
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int n,m,k;
char mp[11][30];
int vis[11][30];
void dfs(int x,int y){
int dep=0;
for(int i=1;i<=20;i++){
int nx=x-i,ny1=y-i,ny2=y+i;
if(nx<1||ny1<1||ny2>m||mp[nx][ny1]!='*'||mp[nx][ny2]!='*')break;
dep++;
}
if(dep>=k){
vis[x][y]=1;
for(int i=1;i<=20;i++){
int nx=x-i,ny1=y-i,ny2=y+i;
if(nx<1||ny1<1||ny2>m||mp[nx][ny1]!='*'||mp[nx][ny2]!='*')break;
vis[nx][ny1]=1;vis[nx][ny2]=1;
}
}
}
int main(){
int t;
cin>>t;
while(t--){
cin>>n>>m>>k;
for(int i=1;i<=n;i++)cin>>mp[i]+1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)vis[i][j]=0;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(mp[i][j]=='*'){
dfs(i,j);
}
}
}
int f=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(mp[i][j]=='*'&&!vis[i][j])f=0;
}
}
if(f)cout<<"YESn";
else cout<<"NOn";
}
return 0;
}
D - Productive Meeting
题意：
一堆人交流，两个人每交流一次他们交流的次数就会少一次（狗头，问最多的交流次数
思路：
贪心
因为我们不希望有人退出会议（退出会议代表选择变少了，更容易出现剩一个人权值很大的情况），因此每次都取拥有最大a[i]的和次大a[i]的两个人开展对话，这样一定是最优的。或者可以每次取最大和最小的。
让交流次数多的人先交流，直到只剩一个人或者都不能交流了
优先队列里直接排序了
代码一：
每次取最大和次大的人交流。
#include<bits/stdc++.h>
#define pii pair<int, int>
#define int long long
using namespace std;
struct node {
int a, b;
}b[200005];
signed main() {
int t;
cin>>t;
while (t--) {
int n;
cin >> n;
priority_queue<pii> q;
for(int i=1; i<=n; i++) {
int x;
cin>>x;
if(x) q.push({x, i});
}
int cnt=0;
while (!q.empty()) {
if (q.size() == 1) break;
pii x=q.top();
q.pop();
pii y=q.top();
q.pop();
++cnt;
b[cnt].a=x.second;
b[cnt].b = y.second;
x.first--;
y.first--;
if (x.first!=0) q.push(x);
if (y.first!=0) q.push(y);
}
cout<<cnt<<endl;
for(int i=1; i<=cnt; i++) cout<<b[i].a<<" "<<b[i].b<<endl;
}
return 0;
}
代码二：
每次选取最大和最小的人谈话， 这样最大的人就会尽可能的小。
用set维护
#include<bits/stdc++.h>
#define pii pair<int, int>
#define int long long
using namespace std;
struct node {
int a,b;
}b[200005];
signed main() {
int t;
cin>>t;
while (t--) {
int n;
cin >> n;
set<pii> s;
for(int i=1; i<=n; i++) {
int x;
cin>>x;
if(x)s.insert({x, i});
}
int cnt=0;
while (!s.empty()) {
if (s.size() == 1) break;
auto it=s.begin();
pii x=*it;
s.erase(it);
it=--s.end();
pii y=*it;
s.erase(it);
++cnt;
b[cnt].a=x.second;
b[cnt].b = y.second;
x.first--;
y.first--;
if (x.first!=0) s.insert(x);
if (y.first!=0) s.insert(y);
}
cout<<cnt<<endl;
for(int i=1; i<=cnt; i++) cout<<b[i].a<<" "<<b[i].b<<endl;
}
return 0;
}
E1. Permutation Minimization by Deque
思路：
要求字典序最小的方案，贪心即可，记录当前序列第一位的值，如果放的值比 front的值小，就放在front，能使字典序变小，否则放在 back
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int n;
int s[200050];
deque<int>d;
int main(){
int t;
cin>>t;
while(t--){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&s[i]);
int pre=s[1];d.push_back(s[1]);
for(int i=2;i<=n;i++){
if(pre>s[i]){
pre=s[i];
d.push_front(s[i]);
}else d.push_back(s[i]);
}
while(!d.empty()){
int x=d.front();
d.pop_front();
printf("%d ",x);
}
printf("n");
}
}
E2. Array Optimization by Deque
思路：
还是贪心的思路，可以证明一定是放在当前最优的位置即可。
考虑用 离散化+线段树维护。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int n;
int s[200050];
vector<int>v;
int tr[800050];
void build(int p,int l,int r){
tr[p]=0;
if(l==r)return;
int mid=l+r>>1;
build(2*p,l,mid);
build(2*p+1,mid+1,r);
}
void update(int p,int l,int r,int x){
if(l==r){
tr[p]++;
return;
}
int mid=l+r>>1;
if(x<=mid)update(2*p,l,mid,x);
else update(2*p+1,mid+1,r,x);
tr[p]=tr[2*p]+tr[2*p+1];
}
int query(int p,int l,int r,int x,int y){
if(x>y)return 0;
if(x<=l&&r<=y)return tr[p];
int ans=0;
int mid=l+r>>1;
if(x<=mid)ans+=query(2*p,l,mid,x,y);
if(mid<y)ans+=query(2*p+1,mid+1,r,x,y);
return ans;
}
int main(){
int t;
cin>>t;
while(t--){
scanf("%d",&n);
v.clear();
for(int i=1;i<=n;i++)scanf("%d",&s[i]),v.push_back(s[i]);
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
int len=v.size();
build(1,1,len);
ll ans=0;
for(int i=1;i<=n;i++){
int pos=lower_bound(v.begin(),v.end(),s[i])-v.begin();
int res1=query(1,1,len,1,pos);
int res2=query(1,1,len,pos+2,len);
ans+=min(res1,res2);
update(1,1,len,pos+1);
}
printf("%lldn",ans);
}
}
F. Array Stabilization (AND version)
思路：
相当于序列循环变换 长度为d，因为是 与操作，原来是0的位置之后还是0，循环变换之后 ，0可以去改变1，用 bfs 模拟实现即可。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int n,d;
queue<int>q;
int vis[1000050];
int s[1000050];
int main(){
int t;
cin>>t;
while(t--){
scanf("%d%d",&n,&d);
for(int i=0;i<n;i++){
scanf("%d",&s[i]);
if(s[i])vis[i]=1e9;
else vis[i]=0,q.push(i);
}
while(!q.empty()){
int x=q.front();q.pop();
int nex=(x+d)%n;
if(vis[nex]>vis[x]+1){
vis[nex]=vis[x]+1;
q.push(nex);
}
}
int ans=0;
for(int i=0;i<n;i++){
ans=max(ans,vis[i]);
}
if(ans==1e9)printf("-1n");
else printf("%dn",ans);
}
}
G. Minimal Coverage
很好的一道题目，有一个
d
p
dp
dp优化小技巧。
题意:
有
1
e
4
1e4
1e4个线段，要把他们按顺序放在一维数轴上，第一个随便放，接下来的线段的起点必须从上一个线段的终点开始，左右方向无所谓，要求总覆盖的长度最小
思路：
首先考虑状态转移，设三维状态
d
p
[
i
]
[
j
]
[
k
]
dp[i][j][k]
dp[i][j][k]，分别枚举起点、下界和上界，覆盖的长度就是 上界 - 下界。但是三维的状态肯定会 T。
考虑优化掉一维状态。
我们可以固定下界，这样 dp 转移就是多起点转移了，但是多起点很容易实现，多设置一些初始状态即可。这样我们只需要记录以
i
i
i 作为起点的最小上界去转移。
像这种下界是 枚举量，起点是过程量，我们可以考虑用平移、固定下界的方法省去一维 dp；
代码：
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int n,d;
int s[10050];
int dp[10050][2060];
int main(){
int t;
cin>>t;
while(t--){
cin>>n;
for(int i=1;i<=n;i++)cin>>s[i];
for(int i=1;i<=n;i++)
for(int j=0;j<=2000;j++)dp[i][j]=1e9;
for(int i=0;i<s[1];i++)dp[1][i]=i+s[1];
for(int i=s[1];i<=2000;i++)dp[1][i]=i;
for(int i=2;i<=n;i++){
for(int j=0;j<=2000;j++){
if(dp[i-1][j]==1e9)continue;
if(j+s[i]<=2000){
dp[i][j+s[i]]=min(dp[i][j+s[i]],max(dp[i-1][j],j+s[i]));
}
if(j-s[i]>=0){
dp[i][j-s[i]]=min(dp[i][j-s[i]],max(dp[i-1][j],j));
}
}
}
int ans=1e9;
for(int i=0;i<=2000;i++)ans=min(ans,dp[n][i]);
cout<<ans<<endl;
}
}
最后
以上就是害羞蜻蜓为你收集整理的Codeforces Round #744 (Div. 3) 解题报告A. Casimir’s String SolitaireB. Shifting SortC. TicksD - Productive Meeting的全部内容，希望文章能够帮你解决Codeforces Round #744 (Div. 3) 解题报告A. Casimir’s String SolitaireB. Shifting SortC. TicksD - Productive Meeting所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复