本文由首席特约审稿人 @寒歌 独家冠名审稿。
首先从整数的快速幂谈起,所谓整数快速幂指的是
![]()
的高效计算。传统的做法是通过
![]()
次迭代循环相乘得到,即
它的复杂度是
![]()
。事实上我们有
![]()
的算法,其核心思想是将
![]()
表为二进制,即令
![]()
,其中
![]()
。这样利用幂的运算法则我们有
![]()
,而其中的
![]()
可以由
![]()
平方得到,而二进制表示的每一位
![]()
控制答案要不要乘上
![]()
。仍然通过迭代循环计算,不过循环的次数由原来的
![]()
变成了
![]()
的二进制表示的位数
![]()
,所以这种做法的复杂度是
![]()
,参考代码如下。
ps:上面的推导中要注意一个初中数学问题,
![]()
和
![]()
的值一般不同,这是因为
![]()
,而
![]()
和
![]()
一般不等,所以不要简写作可能引起歧义的
![]()
。
如果我们把整数的乘法换成矩阵的乘法,就能推广到矩阵的快速幂。矩阵快速幂实际上应该叫方阵快速幂,因为
![]()
的两个矩阵能够相乘的前提是
![]()
,那么能与自己相乘的
![]()
矩阵必须满足
![]()
。
算法题中用代码实现矩阵快速幂,首先要实现矩阵乘法,写法有很多,但毕竟二维数组表示的矩阵,参与返回值传递比较麻烦,所以我一般采用三个参数——矩阵
![]()
地址、矩阵
![]()
地址、结果矩阵地址(如果矩阵维数不能确定,再多传入一个矩阵维数),而不是把整个结果作为返回值,参考代码如下。
有了矩阵的乘法,就可以类似地实现矩阵快速幂了,原理和整数快速幂相同,参考代码如下。
以这种方式,求
![]()
维矩阵的
![]()
次幂,会先调用
![]()
次矩阵乘法,再调用两重
![]()
循环。其中每次矩阵乘法有一个三重
![]()
循环和一个两重
![]()
循环,因此总复杂度
![]()
(事实上矩阵乘法的
![]()
算法还能优化,但我们用到的矩阵一般都不太大,就没有这个必要了)。
矩阵快速幂的一个简单应用是求
![]()
数列的第
![]()
项
![]()
。传统的做法是使用
![]()
在
![]()
的复杂度下完成(
![]()
),而对于
![]()
以上的数量级,这种做法就会导致超时,这时候就可以使用矩阵快速幂来优化
![]()
的时间复杂度。我们看到递推式中
![]()
总是前两项
![]()
的线性表示,那么就可以尝试构造下面的等式,希望每次矩阵乘法都能把
![]()
变成它的后一项
![]()
。
那么根据矩阵乘法的规则以及递推表达式,可以填充部分问号的内容,如下所示。
那么
![]()
的位置,当然希望乘法以后同等地得到
![]()
,即
根据乘法的规则,我们又可以填充常数矩阵的两个问号,即
剩下四个问号发现没有影响,全填零就好了。
事实上,最后填的四个零对原问题没有作用,上式可以简写为向量与矩阵的乘法如下。
从而有下面的结论:
如此就把原问题转化为求矩阵的幂,利用前面的矩阵快速幂算法可以把复杂度降到
![]()
,这样即使是
![]()
的数量级也能轻松在
![]()
内完成。
回顾前面填充等式的过程,我们可以总结出,对于每一项是前面若干项的线性组合的递推关系,我们总可以类似地构造“与常矩阵相乘”的运算来表示一次递推,其中的常矩阵由矩阵乘法的规则一步步导出,最后就可以把
![]()
次运算的递推转化为
![]()
次运算的矩阵快速幂。
下面来看一道具体的算法题应用。
给定
![]()
个
![]()
面分别相对的骰子,面与面对齐垒成一根长柱,事先给定
![]()
对数
![]()
,要求贴合的两面不能是某对
![]()
,问所有不同垒法的方案数。输入的第一行是两个数
![]()
,接下来
![]()
行,每一行是两个数
![]()
,其中
![]()
,由于答案很大,对
![]()
取模。
首先侧面可以旋转,因此可以不考虑侧面,最终答案乘上
![]()
即可(这里还是有争议的,如果旋转四个方向看作同一种垒法,只需要乘上
![]()
,具体哪种只要试样例就好了)。
既然忽略了侧面,我们便只需要考虑顶面(底面和顶面的数字一一对应),因为不能贴合的数字是由输入决定的,所以顶面数字
![]()
地位不对等,这暗示我们要分六类讨论。因此可以想到二维
![]()
——
![]()
,用
![]()
表示垒
![]()
个骰子,且最上面的骰子顶面数字是
![]()
的子问题的答案。
如果没有
![]()
条限制,显然垒
![]()
个骰子只要在垒
![]()
个骰子的基础上放上一个骰子就行了,与垒
![]()
个骰子中最上面骰子的顶面无关,即
![]()
。用前面的方法构造下面的等式。
根据递推式,可以继续填充如下。
继续填充,填满并改写为向量的形式,可得
而显然
![]()
,自然有
而要求的答案为
![]()
,只要把转移矩阵的
![]()
次方的每个元素相加,得到的和再乘上
![]()
就可以了。
再考虑
![]()
对不能紧贴的数字,仔细想想其实就是递推式中有些项不再需要相加,放在转移矩阵中就是有些元素要置零。具体是哪些元素置零呢?对于其中某组不能贴合的数
![]()
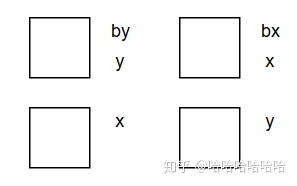
,有下面两种摆法是需要去掉的。
如果一个骰子顶面是
![]()
,那么它上面那个骰子顶面不能是
![]()
的背面
![]()
;如果一个骰子顶面是
![]()
,那么它上面那个骰子顶面不能是
![]()
的背面
![]()
。这就引导我们写一个函数计算某一面背面的数字。
要想通过转移矩阵得到上一层以
![]()
为顶面的答案,应该在转移矩阵的第
![]()
行找,要想在递推式中去掉下层顶面为
![]()
的情况,就应该把转移矩阵的第
![]()
行第
![]()
列的元素置零。同理还应该把第
![]()
行第
![]()
列的元素置零。可以写出以下代码。
然后实现一下矩阵乘法和矩阵快速幂,如下所示。
因为也需要计算
![]()
,补一个整数快速幂,然后计算答案就好了,完整代码如下。
完结撒花,最后,点击一下下面的【❤】和【⭐】。
最后
以上就是火星上摩托最近收集整理的关于二进制矩阵乘法_从矩阵快速幂到一类DP的时间复杂度优化的全部内容,更多相关二进制矩阵乘法_从矩阵快速幂到一类DP内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。









发表评论 取消回复