矩阵快速幂优化DP-染砖问题

56 阅读 0 评论 37 点赞

我是靠谱客的博主曾经月饼，最近开发中收集的这篇文章主要介绍矩阵快速幂优化DP-染砖问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目描述:

衣食无忧的 Q老师有一天突发奇想，想要去感受一下劳动人民的艰苦生活。
具体工作是这样的，有 N 块砖排成一排染色，每一块砖需要涂上红、蓝、绿、黄这 4 种颜色中的其中 1 种。且当这 N 块砖中红色和绿色的块数均为偶数时，染色效果最佳。
为了使工作效率更高，Q老师想要知道一共有多少种方案可以使染色效果最佳，你能帮帮他吗？

Input

第一行为 T，代表数据组数。(1 ≤ T ≤ 100)
接下来 T 行每行包括一个数字 N，代表有 N 块砖。(1 ≤ N ≤ 1e9)

Output

输出满足条件的方案数，答案模 10007。

Sample Input

2
1
2

Sample Output

2
6

思路:

连续格子染色，有子结构特征，考虑DP
状态:

f[0][i]染色i块砖 红绿块数均为偶数的方案数
f[1][i]染色i块砖 红绿块数 有一个为奇数， 有一个为偶数的方案数
f[2][i]染色i块砖 红绿均为奇数得到方案数

状态转移:

f[0][i] = 2 * f[0][i-1] + f[1][i-1]
f[1][i] = 2 * f[0][i-1] + 2 * f[1][i-1] + 2 * f[2][i-1]
f[2][i] = f[1][i-1] + 2 * f[2][i-1]
初始状态:
f[0][0] = 1 f[1][0] = 0 f[2][0] = 0

写成矩阵形式即可利用快速幂转换
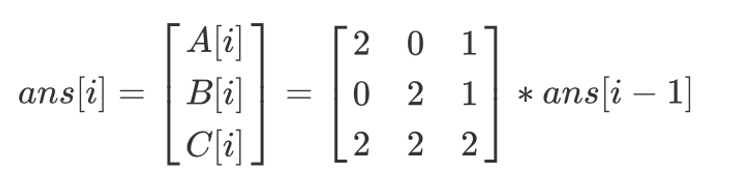
在这里插入图片描述
复杂度:O(log(n))

代码：

#include <iostream>
#include <cstring>
using namespace std;
const int p = 10007;
const int N = 3;
struct Matrix
{
 int a[N][N];
 Matrix operator *(const Matrix& m)const 
 {
  Matrix ret;
  for(int i = 0; i < N; i++)
  {
   for(int j = 0; j < N; j++)
   {
    ret.a[i][j] = 0;
    for(int k = 0; k < N; k++)
    {
     ret.a[i][j] += (a[i][k] * m.a[k][j])%p;
     ret.a[i][j] %= p;
    }
   }
  }
  return ret;
 }
 Matrix(){memset(a, 0, sizeof(a));}
 Matrix(const Matrix& m){memcpy(a, m.a, sizeof(a));}
};
Matrix quick_pow(Matrix m, int n)
{
 Matrix ans;
 for(int i = 0; i < N; i++)
  ans.a[i][i] = 1;//初始单位矩阵 
 while(n != 0)
 {
  if(n & 1)
   ans =  ans * m;
  m = m * m;
  n = n >> 1;
 }
 return ans;
}
//f[0][i]染色i块砖 红绿块数均为偶数的方案数
//f[1][i]染色i块砖 红绿块数 有一个为奇数， 有一个为偶数的方案数
//f[2][i]染色i块砖 红绿均为奇数得到方案数 
int main()
{
 Matrix m;
 m.a[0][0] = 2; m.a[0][1] = 1; m.a[0][2] = 0;
 m.a[1][0] = 2; m.a[1][1] = 2; m.a[1][2] = 2;
 m.a[2][0] = 0; m.a[2][1] = 1; m.a[2][2] = 2;
 int f[3] = {1, 0, 0};
 int T;
 cin >> T;
 while(T--)
 {
  int n;
  cin >> n;
  Matrix ans = quick_pow(m, n);
  int res = 0;
  for(int i = 0; i < 3; i++)
  {
   res += ans.a[0][i] * f[i];
   res %= p;
  }
  cout << res << endl;
 } 
}