BZOJ4948: [Wf2017]Airport Construction【线穿多边形】

题目描述：

逆时针方向给出一个简单多边形，问内部可放置的线段的最长长度，保证无两边共线。
$n\le 200$

题目分析：

首先略加思考可以感觉到线段一定过多边形的某两个顶点，但线段的端点不一定是顶点，如下图：

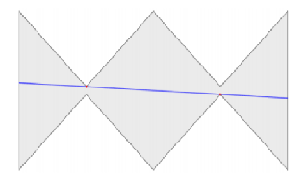
而且线段所在直线可能被多边形截成了几部分：

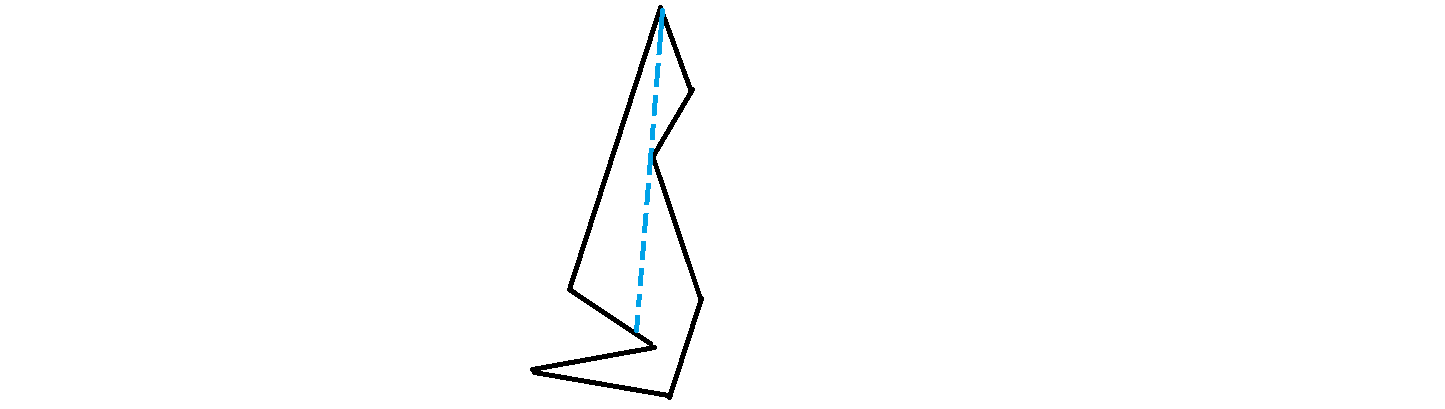
所以需要枚举两个点，求出这条线与多边形所有边的交点，然后按坐标排序，然后将在多边形内部的连续线段考虑进答案。
检验线段是否在多边形内部，判断线段中点是否在多边形内部即可。
判断点是否在多边形内部的方法：
如果是凸多边形，用叉积判断点是否在边的同一方向。
如果是任意多边形，从点引一条向左的平行于x轴的射线，与线段的交点个数如果为奇数就在多边形内部。（如果与顶点相交只计一次，将边摆为上下后用叉积判断是否在左边，忽略与射线平行的边）

另外一种方法代码复杂度较低，这样考虑：

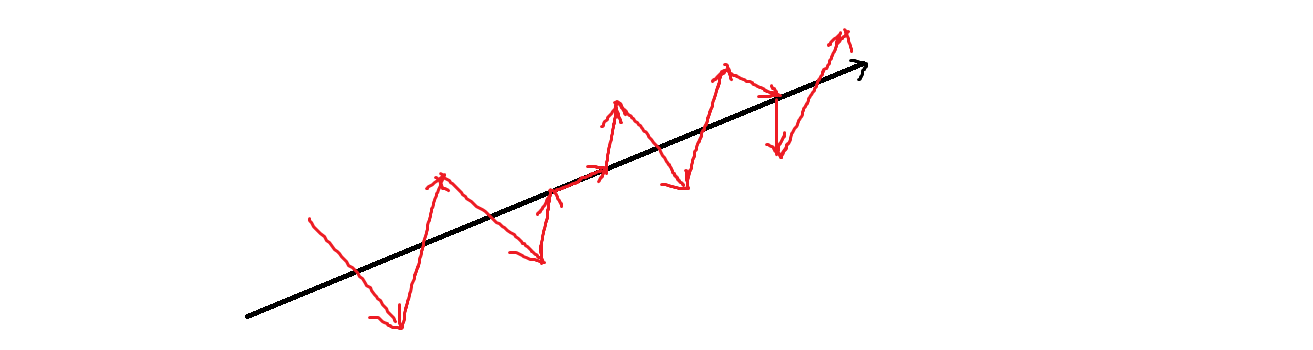
把与直线相交的几条边拿出来看，设形成直线的两个端点为$a,b$，某条边的两个端点为$x,y$（逆时针方向），记$s_1=sgn((b-a)\times (x-a)),s_2=sgn((b-a)\times (y-a))$，$sgn$ 的值域是 { − 1 , 0 , 1 } {-1,0,1} {−1,0,1}
若$s_1=s_2$，跳过。
若$s_1>s_2$，则记这个点的权值为$s_1{s}_2\ne 0?2:1$
若$s_1<s_2$，则记这个点的权值为$s_1{s}_2\ne 0?-2:-1$
（实际上就是 $s_1-s_2$）
如果经过的点的权值和$\ne 0$，那么接下来的一段就一定是在多边形的内部。（逆时针考虑，第一条线的左侧一定在内部）

再求出每个交点到$a$的距离，相减即可得每一段线段的长度。
求交点到$a$的距离和求交点类似，通过正弦定理简单叉积即可（见代码），可以看看oi-wiki上求交点的做法。

Code：

#include<bits/stdc++.h>
#define maxn 205
using namespace std;
const double eps = 1e-9;
int n;
double ans;
int sgn(double x){return x>eps?1:x<-eps?-1:0;}
struct Point{
	double x,y; Point(double x=0,double y=0):x(x),y(y){}
	Point operator - (const Point &p){return Point(x-p.x,y-p.y);}
	Point operator + (const Point &p){return Point(x+p.x,y+p.y);}
	double operator * (const Point &p){return x*p.y-y*p.x;}
	double len(){return sqrt(x*x+y*y);}
}a[maxn];
struct Line{
	Point p,v;
	Line(Point p,Point v):p(p),v(v){}
};
double Length(Line a,Line b){
	return b.v*(a.p-b.p)/(a.v*b.v)*a.v.len();
}
pair<double,int>P[maxn];
void solve(Line L){
	int cnt=0;
	for(int i=1;i<=n;i++){
		int d1=sgn(L.v*(a[i]-L.p)),d2=sgn(L.v*(a[i+1]-L.p));
		if(d1==d2) continue;
		P[++cnt]=make_pair(Length(L,Line(a[i],a[i+1]-a[i])),(d1>d2?1:-1)*(d1&&d2?2:1));
	}
	sort(P+1,P+1+cnt);
	int flg=0; double len=0;
	for(int i=1;i<=cnt;i++){
		if(flg) len+=P[i].first-P[i-1].first;
		else ans=max(ans,len),len=0;
		flg+=P[i].second;
	}
	ans=max(ans,len);
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%lf%lf",&a[i].x,&a[i].y); a[n+1]=a[1];
	for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) solve(Line(a[i],a[j]-a[i]));
	printf("%.9fn",ans);
}

最后

以上就是贪玩马里奥为你收集整理的BZOJ4948: [Wf2017]Airport Construction【线穿多边形】的全部内容，希望文章能够帮你解决BZOJ4948: [Wf2017]Airport Construction【线穿多边形】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。