双指针算法详解+4例题

双指针算法模板：

for (int i = 0, j = 0; i < n; i ++ )
{
    while (j < i && check(i, j)) j ++ ;
	// 具体问题的逻辑
}

常见问题分类：
(1) 对于一个序列，用两个指针维护一段区间
(2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

详见例题：

1.奶牛拍照：

农夫约翰有 N头奶牛，编号 1∼N。

约翰让它们排成一排，以便拍照。

最初，奶牛从左到右按照 a1,a2,…,aN 的顺序排列。

但是，约翰希望奶牛从左到右按照 b1,b2,…,bN 的顺序排列。

为此，他需要对队列进行一系列的调整操作。

每次操作可以选择任意一头奶牛并将其向左移动一些位置。

请问，至少需要多少次操作，才能使奶牛按照约翰满意的顺序排列。

输入格式

第一行包含整数 NN。

第二行包含 a1,a2,…,aN，这是一个 1∼N的排列。

第三行包含 b1,b2,…,bN，这是一个 1∼N 的排列。

输出格式

一个整数，表示所需的最少操作次数。

数据范围

1≤N≤105

输入样例1：

5
1 2 3 4 5
1 2 3 4 5

输出样例1：

0

样例1解释

本样例中，奶牛已经按照约翰满意的顺序排列，因此无需任何操作。

输入样例2：

5
5 1 3 2 4
4 5 2 1 3

输出样例2：

2

样例2解释

在本样例中，至少需要 22 次操作，具体如下：

1. 让奶牛 4 向左移动 4 位。
2. 让奶牛 2 向左移动 2 位。

队列变化如下：

   5 1 3 2 4
-> 4 5 1 3 2
-> 4 5 2 1 3

思路：

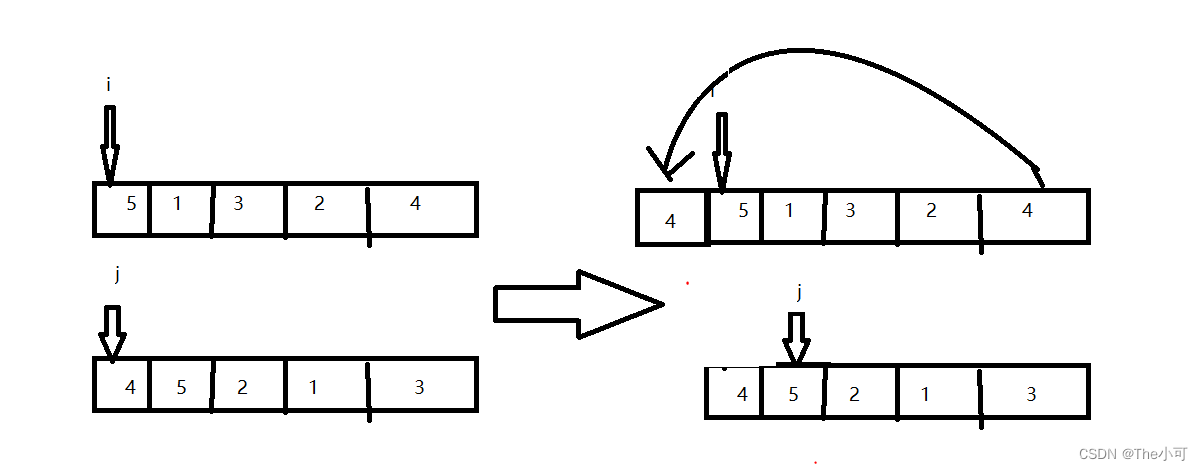
1. i 指针指向 a[0] , j 指针指向b[0],
2. 以b数组作为模板，只要 a[i]!=b[j] 我们就一定可以在a数组找到一个相等的数并把它移动到a数组的最前面 ( j 指针并不是与当前i指针指向的数相等，所以 i指针 指向不变 )
3. 标记一下 这个找到的数b[j]，防止重复找.
4. 在b数组上的数一定可以在a数组上找到，不论 a[i] 是否等于 b[j] 都将 j指针指向下一个 j++
5. 如果 a[i]==b[j] 继续往后移，i指针与j指针指向的数相等， i++

#include<iostream>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
bool v[N];  //
int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++)cin>>a[i];
    for(int i=0;i<n;i++)cin>>b[i];
    int ans=0;
    for(int i=0,j=0;i<n&&j<n;j++){
        while(v[a[i]])i++;  //找到第一个没有别标记的数
        if(a[i]!=b[j]){  //总能在a上找到与 b[j] 相等的数
            ans++;
            v[b[j]]=true;
        }else {
            i++;
        }
    }
    cout<<ans;
    return 0;
}

2.最长连续不重复子序列

给定一个长度为 nn 的整数序列，请找出最长的不包含重复的数的连续区间，输出它的长度。

输入格式

第一行包含整数 nn。

第二行包含 nn 个整数（均在 0∼1050∼105 范围内），表示整数序列。

输出格式

共一行，包含一个整数，表示最长的不包含重复的数的连续区间的长度。

数据范围

1≤n≤1051≤n≤105

输入样例：

5
1 2 2 3 5

输出样例：

3

思路：

1. 标记一下每个数的次数，维护 [ j , i ] 区间
2. 若 v[ q[i] ]>1就说明有一个数重复了，我们只需缩小区间( j++ )，直到q[i]==1

参考代码：

121

3.目标数组的和

给定两个升序排序的有序数组 A 和 B，以及一个目标值 x。

数组下标从 0 开始。

请你求出满足 A[i]+B[j]=x 的数对 (i,j)。

数据保证有唯一解。

输入格式

第一行包含三个整数 n,m,x，分别表示 A 的长度，B 的长度以及目标值 x。

第二行包含 n 个整数，表示数组 A。

第三行包含 m 个整数，表示数组 B。

输出格式

共一行，包含两个整数 i 和 j。

数据范围

数组长度不超过 105。
同一数组内元素各不相同。
1≤数组元素≤109

输入样例：

4 5 6
1 2 4 7
3 4 6 8 9

输出样例：

1 1

思路：

1. i 指针从 a数组 从前往后 开始遍历
2. j 指针从 b数组 从后往前 开始遍历
3. 若 a[i]+b[j]>k 说明要缩小区间使和变小 即 j–，反之i++

参考代码：

#include<iostream>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int main(){
    int n,m,k;
    cin>>n>>m>>k;
    for(int i=0;i<n;i++)cin>>a[i];
    for(int i=0;i<m;i++)cin>>b[i];
    for(int i=0,j=m-1;i<n;i++){
        while(a[i]+b[j]>k)j--;
        if(a[i]+b[j]==k){
            cout<<i<<" "<<j;
            break;
        }
    }
    return 0;
}

4.判断子序列

给定一个长度为 n 的整数序列 a1,a2,…,an 以及一个长度为 m 的整数序列 b1,b2,…,bm。

请你判断 a 序列是否为 b 序列的子序列。

子序列指序列的一部分项按原有次序排列而得的序列，例如序列 {a1,a3,a5} 是序列 {a1,a2,a3,a4,a5} 的一个子序列。

输入格式

第一行包含两个整数 n,m。

第二行包含 n 个整数，表示 a1,a2,…,an。

第三行包含 m 个整数，表示 b1,b2,…,bm。

输出格式

如果 a 序列是 b 序列的子序列，输出一行 Yes。

否则，输出 No。

数据范围

1≤n≤m≤105,
−109≤ai,bi≤109

输入样例：

3 5
1 3 5
1 2 3 4 5

输出样例：

Yes

题解：

#include<iostream>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++)cin>>a[i];
    for(int i=0;i<m;i++)cin>>b[i];
    for(int i=0,j=0;i<m;i++){
        if(b[i]==a[j])j++;
        if(j==n){
            cout<<"Yes";
            return 0;
        }
    }
    cout<<"No";
    return 0;
}

最后

以上就是长情御姐为你收集整理的双指针算法详解+4例题的全部内容，希望文章能够帮你解决双指针算法详解+4例题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。