「数据结构」算法分析

原文发布于Hibiki33’s Blog，转载请标明出处。

算法效率的度量

同一个算法用不同语言实现，或者用不同的编译程序进行编译，或者在不同的计算机上运行时，效率均不相同。这表明使用绝对的时间单位衡量算法的效率是不合适的。

抛开其他因素，可以认为一个特定算法“运行工作量”的大小，只依赖于问题的规模，即问题规模的函数。

时间复杂度

算法时间

算法时间是控制结构（顺序、分支和循环）和原操作（固有数据类型的操作）的综合结果。

通常的做法是，从算法中选取一种对于所研究的问题（或算法类型）来说是基本操作的原操作，以该基本操作 重复执行的次数 作为算法的时间量度。例如下面这题：

• 给你一个非空整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

• 例如：输入数组大小 5 ，输入数组 4 1 2 1 2 ，输出结果 4

我们很容易想到这种做法：

for (i = 0; i < n; i++)
{
    for (j = 0; j < n; j++)
    {
        if ((nums[i] == nums[j]) && (i != j))
        {
            break;
        }
        if (j == n - 1) 
        {
            printf("%d", nums[i]);
        }
    }
}

依次用每个数与整个数组各数相比较，出现相等情况则直接进行下一个数与数组各数相比较，直到出现一个数与数组所有数都不相等的情况。不难看出，整个算法执行的时间与该基本操作重复执行的次数 $n^2$ 成正比。

但是，我们还可以用位运算解决：

int ans = 0;
for (i = 0; i < n; i++)
{
    ans = ans ^ nums[i];
}
printf("%d", ans);

两个相同数进行异或运算结果为0；任意数与0异或结果就为这个任意数。整个算法执行的时间与该基本操作重复执行的次数 $n$ 成正比。

从上面的例子我们可以看出算法对于问题解决时间的影响。

时间复杂度的定义

一般情况下，算法中基本操作重复执行的次数是问题规模 $n$ 的某个函数 $f(n)$ ，算法的时间量度记作

$$T(n)=O(f(n))$$

它表示随问题规模 $n$ 的增大，算法执行时间的增长率和 $f(n)$ 的增长率相同，称作算法的 渐进时间复杂度(asymptotic time complexity) ，简称 时间复杂度 。

频度到复杂度

多数情况下，问题的基本操作的原操作是最深层循环内的语句中的原操作，它的循环次数和包含它的语句的频度相同。语句的频度指的是该语句重复执行的次数。

下列三个程序段中：

1. i++; a = 0
2. for (i = 0; i < n; i++)
3. for (i = 0; i < n; i++) { for (j = 0; j < n; j++) }

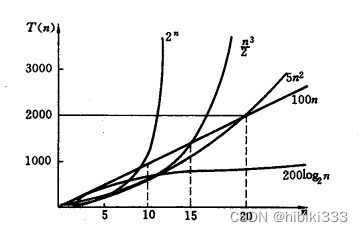
含基本操作“自增1”的语句频度分别为 1、 $n$ 和 $n^2$ ，则这三个程序段的时间复杂度分别为 $O(1)$ 、$O(n)$ 和 $O(n^2)$ ，分别成为常量阶、线性阶和平方阶。还可能有对数阶 $O(logn)$ 、指数阶 $O(2^n)$等。我们应该尽可能选用多项式阶 $O(n^k)$ 的算法，而不希望用指数阶的算法。

空间复杂度

类似于算法的时间复杂度，我们以 空间复杂度(space complexity) 作为算法所需存储空间的量度，记作
$$S(n)=O(f(n))$$
一个上机执行的程序除了需要存储空间来寄存本身所用指令、常数、变量和输入数据外，也需要一些对数据进行操作的工作单元和存储一些为实现计算所需信息的辅助空间。若输入数据所占空间只取决于问题本身，和算法无关，则只需要分析除输入和程序之外的额外空间，否则应同时考虑输入本身所需空间。

例如上述寻找不成对数的题目，考虑输入本身所需的空间，则空间复杂度为$O(n)$；若不考虑输入本身所需的空间，则为$O(1)$。额外空间相对于输入数据量来说是常数，则称此算法为原地工作或原地算法。

[1] 对于 $O(n)$ 中大写O的定义，可以回忆数学分析中的无穷大

最后

以上就是年轻小天鹅为你收集整理的「数据结构」算法分析的全部内容，希望文章能够帮你解决「数据结构」算法分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。