LeetCode 排序数组（八种常见排序算法）

给定一个整数数组 nums，将该数组升序排列。

示例 1：

输入：[5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：[5,1,1,2,0,0]
输出：[0,0,1,1,2,5]

提示：

1 <= A.length <= 10000
-50000 <= A[i] <= 50000

$思路分析：$排序问题是算法中最为经典的问题之一，比较常见的大概有八、九种。

$选择排序：$

每次从剩余待排元素中取出最小的元素，整个取数过程就是一个升序序列。时间复杂度O(n²)

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int numsSize = nums.size();
        //每次从剩余待排元素[i, numsSize - 1]中，找到最小元素放到nums[i]
        for (int i = 0; i < numsSize; ++i){
            int minValIndex = i;//在[i, numsSize - 1]中，最小元素的下标
            for (int j = i + 1; j < numsSize; ++j){
                if (nums[j] < nums[minValIndex]){
                    minValIndex = j;//更新最小元素下标
                }
            }
            swap(nums[i], nums[minValIndex]);//将当前最小元素放入nums[i]
        }
        return nums;
    }
};

这道题测试量比较大，超时了。

$冒泡排序：$

每一趟确定一个元素，一趟扫描采取相邻元素比较的形式进行。时间复杂度O(n²)（超时）

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int numsSize = nums.size();
        //每一趟确定一个元素，总共numsSize-1趟
        for (int i = 1; i < numsSize; ++i){
            //每次比较两个相邻元素，出现逆序则交换，就是把大的元素逐渐移动到最后（故名为冒泡）
            for (int j = 0; j + 1 < numsSize; ++j){
                if (nums[j] > nums[j + 1]){//出现逆序，交换
                    int tempVal = nums[j];
                    nums[j] = nums[j + 1];
                    nums[j + 1] = tempVal;
                }
            }
        }
        return nums;
    }
};

$插入排序：$

假设nums[0, i - 1]已经排序好，每次将nums[i]插入已经排序好的段中，因此得名“插入排序”。时间复杂度O(n²)（超时）

class Solution {
public:
	vector<int> sortArray(vector<int>& nums) {
		int numsSize = nums.size();
		//假设nums[0, i - 1]这一段排序好的，每次将nums[i]插入其中
		for (int i = 1; i < numsSize; ++i) {
			int j = i - 1;//每次将nums[i]进行归位
			while (j >= 0 && nums[j] > nums[j + 1]) {
				int tempVal = nums[j + 1];
				nums[j + 1] = nums[j];
				nums[j--] = tempVal;
			}
		}
		return nums;
	}
};

$希尔排序：$

希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

当初我也是弄了好一段时间都无法理解希尔排序，看了无数个图解，然并软。强烈推荐自己跟着代码直接在图上画一下顺序调整的过程。

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int numsSize = nums.size(), d = numsSize / 2;//d为步长，初始化为半个数组长
        while (d > 0){//当步长大于零，才有继续的必要
            //步长为d检测逆序的第一个下标
            for (int i = d; i < numsSize; ++i){
                int j = i;//如果检测到了逆序，则使用下标j，把出现逆序对的这一个队重新扫描一遍
                while (j >= d && nums[j - d] > nums[j]){//出现逆序对（注意下标不能出界）
                    swap(nums[j], nums[j - d]);//交换
                    j -= d;//继续往前推下标j
                }
            }
            d /= 2;//缩小步长
        }
        return nums;
    }
};

$堆排序：$

首先得了解两个概念，大顶堆、小顶堆。

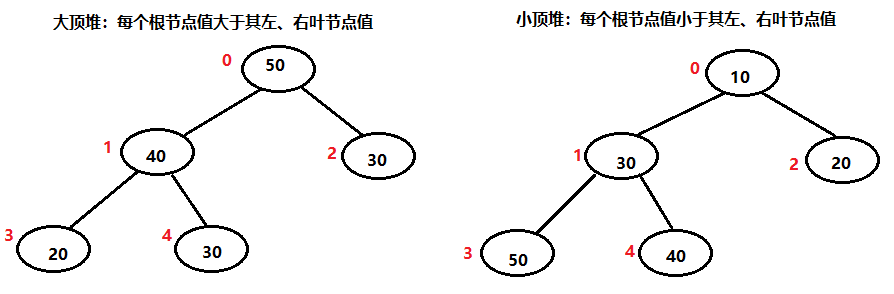
红色的小数字为一维数组的编号，堆排序就是根据这个排序的顺序进行类似“冒泡”的操作，每次将当前待排序的序列中的最值移动到堆顶，然后把最值与最后一个元素交换，从而每次拍好一个元素。
如果是升序排序，则采用大顶堆，每次取出当前待排元素中的最大值，将其与最后一个位置的元素进行交换。
如果是降序排序，则采用小顶堆，每次取出当前待排元素中的最小值，将其与最后一个位置的元素进行交换。

这里还有一个规律，最大的并且有子节点的下标 = (maxIndex - 1) / 2，比如上面的最大下标是4，最大的并且有子节点的下标为1 = (4 - 1) / 2，这并不是偶然，是由满二叉树的性质决定的。

下面将演示升序排序，利用大顶堆结构进行辅助。






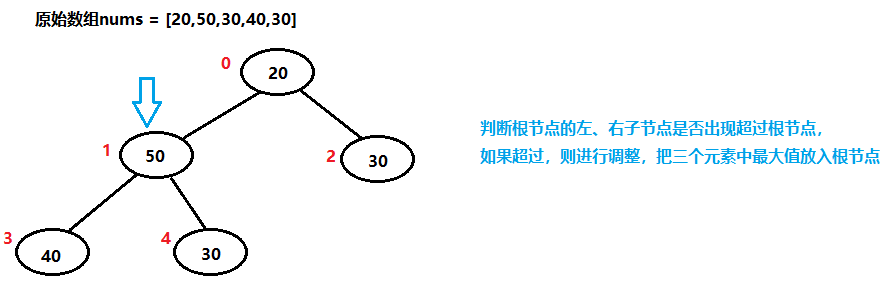
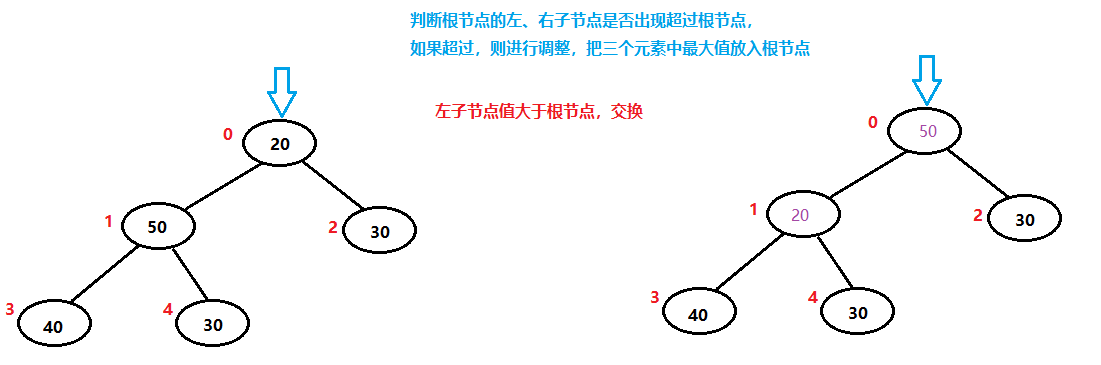
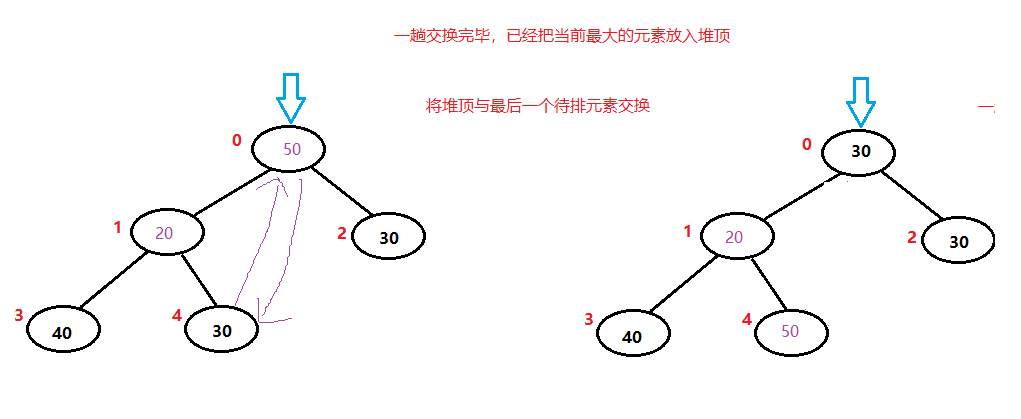
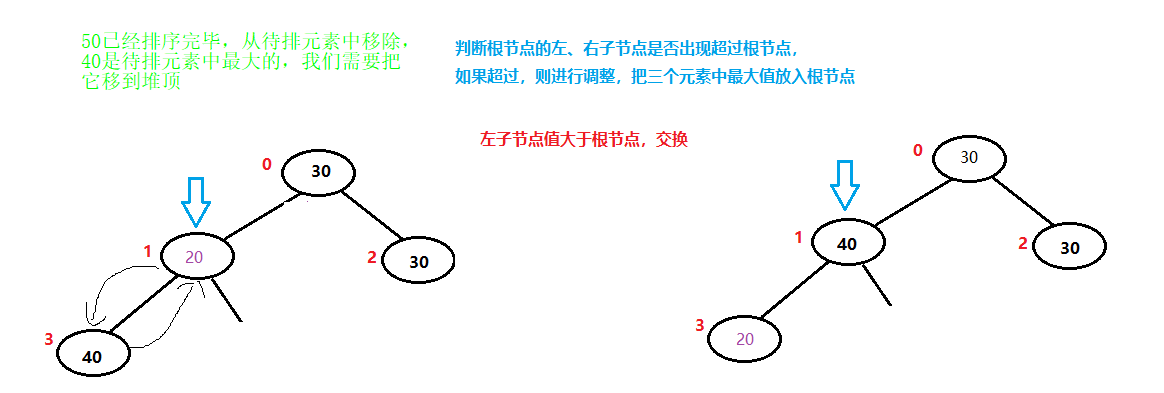
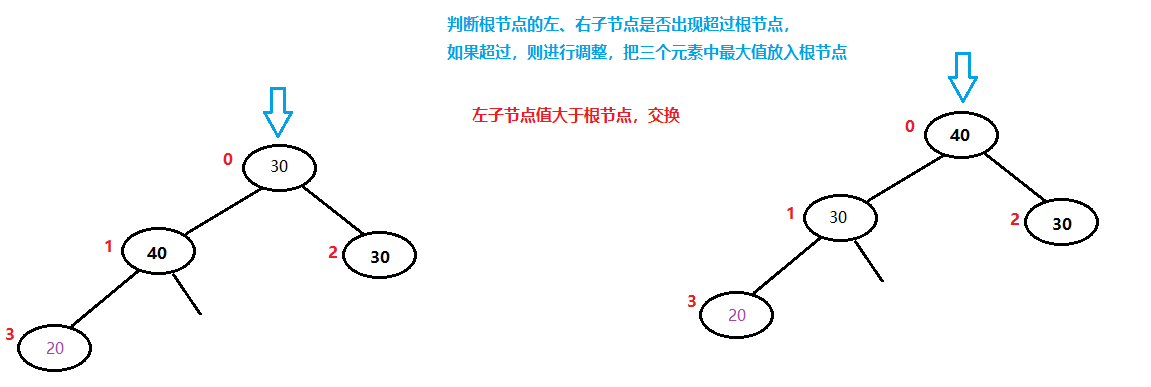
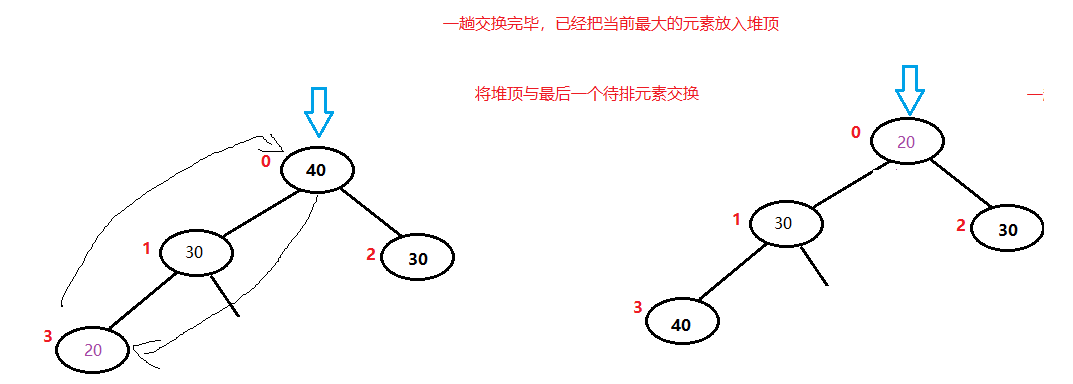
40已经排序完毕，从堆中移除


30排序完毕，从堆中移除

最后全部排序完毕，得到最后结果。

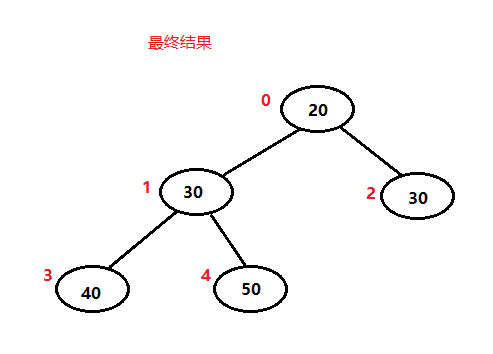
class Solution {
public:
	vector<int> sortArray(vector<int>& nums) {
		//待排序的最后一个元素的下标
		for (int endIndex = nums.size() - 1; endIndex > 0; endIndex -= 1) {
			int firstParent = (endIndex - 1) / 2;//第一个有子节点的节点
			while (firstParent >= 0) {
				//当前根节点与左子节点比较，如果左子节点小于根，交换
				if (nums[firstParent] > nums[firstParent * 2 + 1]) {
					swap(nums[firstParent], nums[firstParent * 2 + 1]);
				}
				//当前根节点与右子节点比较，如果右子节点小于根，交换（注意右子节点需要判断是否超过了待排序的最后一个元素的下标
				if (firstParent * 2 + 2 <= endIndex && nums[firstParent] > nums[firstParent * 2 + 2]) {
					swap(nums[firstParent], nums[firstParent * 2 + 2]);
				}
				firstParent -= 2;
			}
		}
		return nums;
	}
};

其他快排，归并，计数，桶排算法后期有时间再更新

最后

以上就是帅气心锁为你收集整理的LeetCode 排序数组（八种常见排序算法）的全部内容，希望文章能够帮你解决LeetCode 排序数组（八种常见排序算法）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。