【剑指 Offer 14- II. 剪绳子 II】

• 贪心算法
• 大数求余

题目描述

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m - 1] 。请问 k[0]* k[1] *…*k[m - 1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。
答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：

2 <= n <= 1000

解题思路

此题与 面试题14- I. 剪绳子
主体等价，唯一不同在于本题目涉及 “大数越界情况下的求余问题” 。 建议先做上一道题，在此基础上再研究此题目的大数求余方法。

算法流程：

1. 当 n ≤ 3 时，按照规则应不切分，但由于题目要求必须剪成 m > 1 段，因此必须剪出一段长度为 1 的绳子，即返回 n − 1 。
2. 当 n > 3 时，求 n 除以 3 的 整数部分 a 和 余数部分 b （即 n = 3a + b ），并分为以下三种情况（设求余操作符号为 “⊙” ）：

• 当 b = 0时，直接返回 $$3^a\odot 1000000007$$
• 当 b = 1时，要将一个 1 + 3转换为 2+2，因此返回 $$(3^{a-1}\times 4)\odot 1000000007$$
• 当 b = 2 时，返回 $$(3^a\times 2)\odot 1000000007$$

大数求余解法

大数越界： 当 a 增大时，最后返回的 3^a大小以指数级别增长，可能超出 int32 甚至 int64 的取值范围，导致返回值错误。
大数求余问题： 在仅使用 int32 类型存储的前提下，正确计算 x^a对 p 求余（即 x^a ⊙p ）的值。
解决方案： 循环求余 、 快速幂求余 ，其中后者的时间复杂度更低，两种方法均基于以下求余运算规则推出：$$(xy)\odot p=[(x\odot p)(y\odot p)]\odot p$$

1. 循环求余

• 根据求余运算性质推出（∵ 本题中 x<p，∴ x⊙p=x ）：
  $$x^a\odot p=[(x^{a-1}\odot p)(x\odot p)]\odot p=[(x^{a-1}\odot p)x]\odot p$$
• 解析： 利用此公式，可通过循环操作依次求 $$x^1,x^2,...,x^{a-1},x^a$$对 p 的余数，保证每轮中间值 rem 都在 int32 取值范围中。封装方法代码如下所示。
• 时间复杂度 O(N) ： 其中 N = a ，即循环的线性复杂度

# 求 (x^a) % p —— 循环求余法
# python
def remainder(x, a, p):
    rem = 1
    for _ in range(a):
        rem = (rem * x) % p
    return rem

或

# 求 (x^a) % p —— 循环求余法
# java(myself)
public Long reminder(int x, int a, int p){
        Long rem = 1L;  // 用1时会报错：int cannot be converted to java.lang.Long
        for(int i = 0; i < a; i++){
            rem = (rem * x) % p;
        }
        return rem;

    }

2. 快速幂求余

• 根据求余运算性质可推出：
  $$x^a\odot p=(x^2{)}^{a/2}\odot p=(x^2\odot p{)}^{a/2}\odot p$$
• 当 a 为奇数时 a/2 不是整数，因此分为以下两种情况（ ‘’//’’ 代表向下取整的除法）：
  
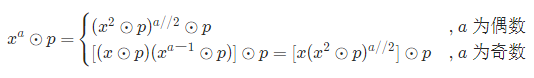
• 解析： 利用以上公式，可通过循环操作每次把指数 a 问题降低至指数 a//2 问题，只需循环 $$lo{g}_2(N)$$次，因此可将复杂度降低至对数级别。封装方法代码如下所示。

# 求 (x^a) % p —— 快速幂求余
# python 
def remainder(x, a, p):
    rem = 1
    while a > 0:
        if a % 2: rem = (rem * x) % p
        x = x ** 2 % p
        a //= 2
    return rem

代码

• Python 代码： 由于语言特性，理论上 Python 中的变量取值范围由系统内存大小决定（无限大），因此在 Python中其实不用考虑大数越界问题。
• Java 代码： $$根据二分法计算原理，至少要保证变量x和rem可以正确存储1000000007^2，而2^{64}>1000000007^2>2^{32}，因此我们选取long类型。$$

class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) return n - 1;
        int b = n % 3, p = 1000000007;
        long rem = 1, x = 3;
        for(int a = n / 3 - 1; a > 0; a /= 2) {
            if(a % 2 == 1) rem = (rem * x) % p;
            x = (x * x) % p;
        }
        if(b == 0) return (int)(rem * 3 % p);
        if(b == 1) return (int)(rem * 4 % p);
        return (int)(rem * 6 % p);
    }
}

或

# 由于语言特性，Python 可以不考虑大数越界问题
class Solution:
    def cuttingRope(self, n: int) -> int:
        if n <= 3: return n - 1
        a, b, p = n // 3, n % 3, 1000000007
        if b == 0: return 3 ** a % p
        if b == 1: return 3 ** (a - 1) * 4 % p
        return 3 ** a * 2 % p   //(b==2)的情况

Python好简单啊！！！之前一直用的java写的，这题我用Java出了个问题才试着用python，这根本不需要考虑大数越界问题，和剪绳子I 那题一样的，只是在后面直接取余即可。

知识点

1. java中如何查看数据类型

//定义getType（）方法
public static String getType(Object o){
    return o.getClass().toString(); //使用int类型的getClass()方法
}
int a = 0;
//获取a的数据类型
System.out.println(getType(a))

2. 大数求余解法(见上)

代码问题（未解决）

我在使用java语言并采用循环求余法对大数进行求余时报错了，具体代码及报错如下：

class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) return n - 1;
        if(n > 3){
            int a = 0, b = 0, p = 1000000007;
            a = n / 3;
            b = n % 3;
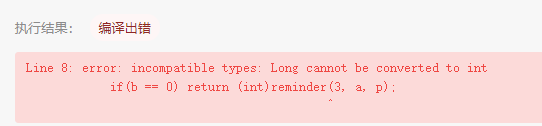
            if(b == 0) return (int)reminder(3, a, p); //类型转换问题出错
            if(b == 1) return (int)((reminder(3, a - 1, p))*4)%p; 
            if(b == 2) return (int)((reminder(3, a, p))*2)%p; 
        }
        return 0;
    }
    public Long reminder(int x, int a, int p){
        Long rem = 1L;  // 用1时会报错：int cannot be converted to java.lang.Long
        for(int i = 0; i < a; i++){
            rem = (rem * x) % p;
        }
        return rem;

    }
}

报错：
Line 8: error: incompatible types: Long cannot be converted to int
if(b == 0) return (int)reminder(3, a, p);

$$疑问：为什么(b==1)和(b==2)时都可使用(int)将Long类型强转为int类型，而(b==0)时不可以呢？$$

作者：jyd
链接：https://leetcode-cn.com/problems/jian-sheng-zi-ii-lcof/solution/mian-shi-ti-14-ii-jian-sheng-zi-iitan-xin-er-fen-f/
来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

最后

以上就是殷勤汉堡为你收集整理的【剑指 Offer 14- II. 剪绳子 II】的全部内容，希望文章能够帮你解决【剑指 Offer 14- II. 剪绳子 II】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。