【LeetCode-剑指Offer】剑指 Offer 56 - II. 数组中数字出现的次数 II

63 阅读 0 评论 42 点赞

我是靠谱客的博主眯眯眼镜子，最近开发中收集的这篇文章主要介绍【LeetCode-剑指Offer】剑指 Offer 56 - II. 数组中数字出现的次数 II，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

一、题目

在一个数组 nums 中除一个数字只出现一次之外，其他数字都出现了三次。请找出那个只出现一次的数字。

示例 1：

输入：nums = [3,4,3,3]
输出：4

示例 2：

输入：nums = [9,1,7,9,7,9,7]
输出：1

限制：

1 <= nums.length <= 10000
1 <= nums[i] < 2^31

二、解决

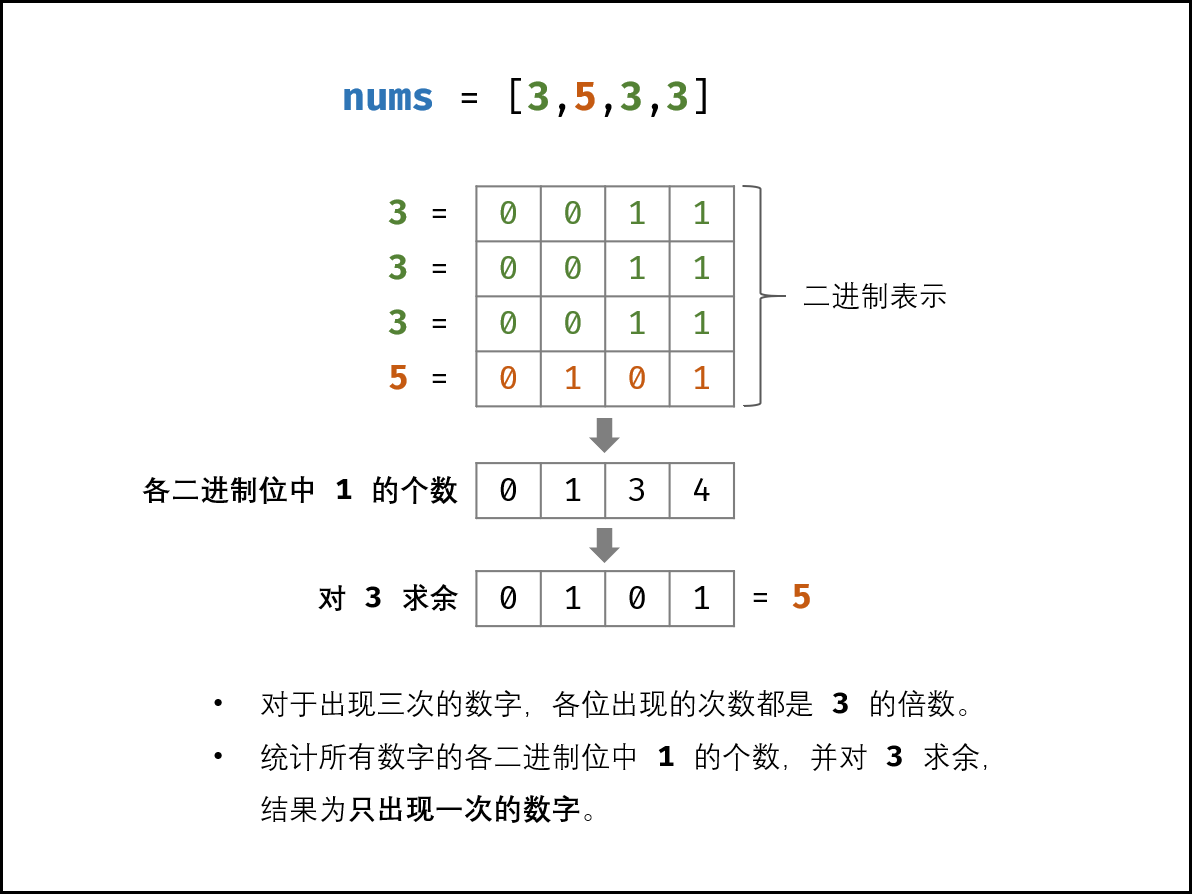
考虑数字二进制形式，对于出现三次的数字，各二进制位出现次数是3的倍数。
因此，统计所有数字的各二进制1的出现次数，并对3求余，结果则为只出现的数字。

1、有限状态自动机

思路：

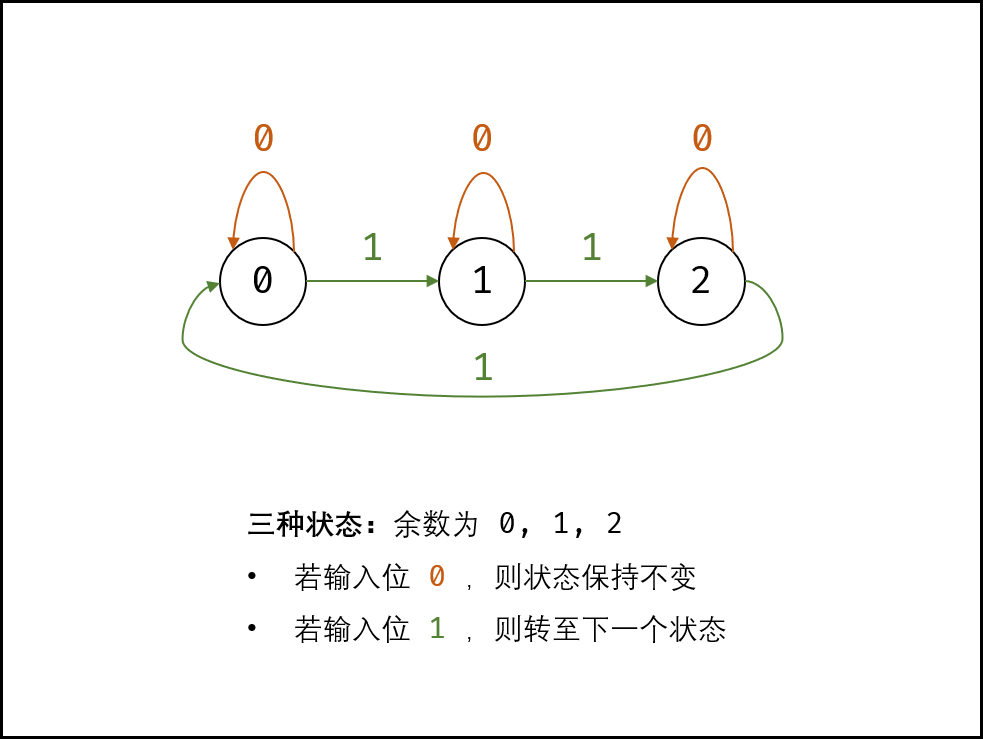
各二进制位的位运算规则相同，因此只需考虑一位即可。如下图所示，对于所有数字中的某二进制位1的个数，存在三种状态，即3的余数0，1，2。

若输入二进制位1，则状态按照右边顺序装换：0–>1–>2–>0–>…
若输入二进制位0，则状态不变。

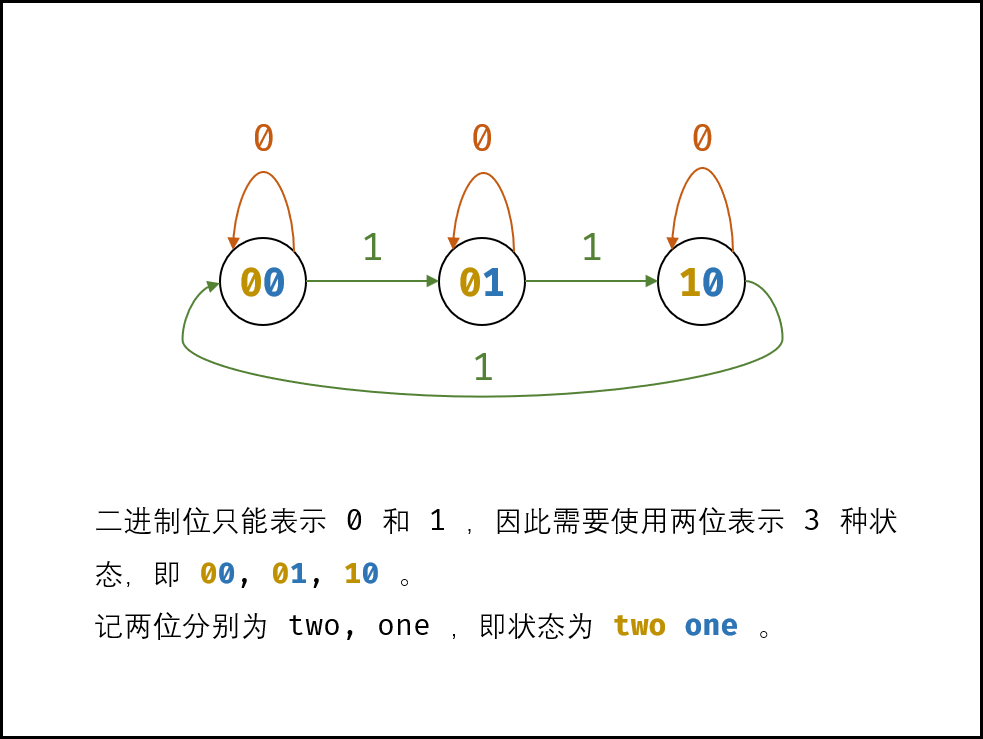
由于二进制只能表示为0，1，因此需要用两个二进制位来表示3个状态。设此两位分别two、one，则状态转换为：
[0 --> 1 --> 2 --> 0 --> …]
00 --> 01 --> 10 --> 00 --> …

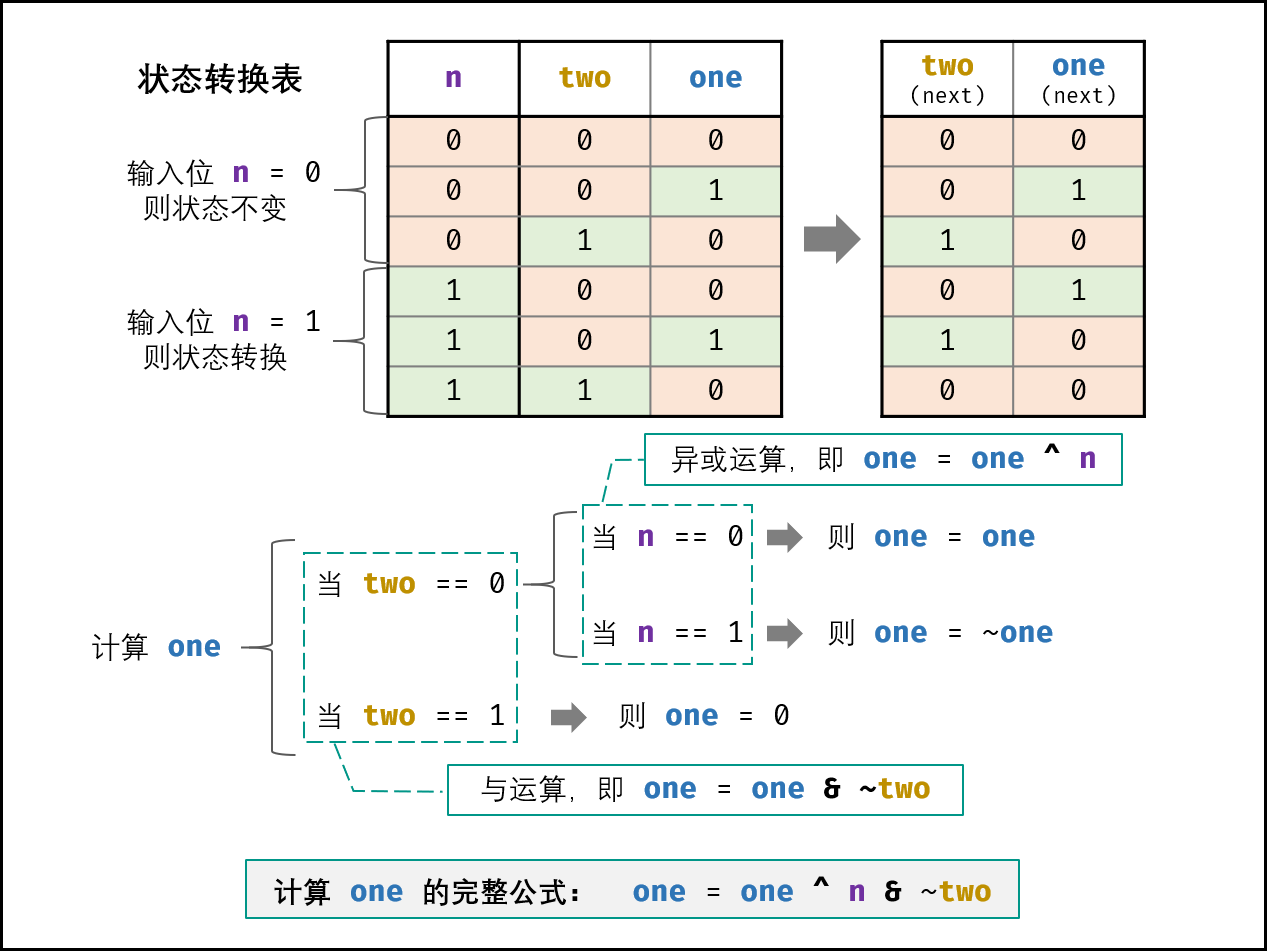
接下来需要通过状态转换表导出状态转换的计算公式。首先回忆下，对于任意二进制位x，有：

异或：x ^ 0 = x,    x ^ 1 = ~x
与：  x & 0 = 0,    x & 1 = x

计算one方法

设当前状态为two-one，此时输入二进制位n。对状态表情况进行拆分，计算如下：

if two == 0
  if n == 0
    one = one
  if n == 1
    one = ~one

if two == 1
   one = 0

引入异或运算简化，可将上面拆分简化：

if two == 0
    one = one ^ n
if two == 1
    one = 0

引入与运算，可进一步简化：

one = one ^ n & ~two

two计算方法

00 +1 = 01
10 +1 = 00
if one == 0
  if n == 0
    two = two
  if n == 1
    two = 0 = ~n

-->简化：（异或运算：0 不变，1 相反-结果与输入相反）
if one == 0
    two = two ^ n 
    
01 +0 = 01
   +1 = 10
if one == 1
  if n == 0
    two = two
  if n == 1
    two = 1 = ~two
    
-->简化：
if one = 1
    two = two ^ n

现在：01  求状态：10
// 输入  twos = 0, ones = 1, n = 1
 ones = ones ^ num & ~twos // 得到 ones = 0
 twos = twos ^ num & ~ones // 得到 twos = 1
// 输出  twos = 1, ones = 0

引入与运算，可进一步简化：

two = two ^ n & ~one

返回值：

以上是对数字的二进制中“一位”的分析，而 int 类型的其他31位具有相同的运算规则，因此可将以上公式直接套用在32位数上。

例证：可以看参考1中幻灯片，再附一个例子，演示各个二进制位变化。

[3,  4,   3,   3]
011，100，011，011

two one 
0   1   (右数第1个二进制位)
0   1
1   0
0  <0>

0   1   (右数第2个二进制位)
0   1
1   0
0  <0>

0   1   (右数第3个二进制位)
0   1
0   1
0  <1>

最后 ones：100 = 4

代码：

class Solution {
    public int singleNumber(int[] nums) {
        int ones = 0, twos = 0;
        for(int num : nums){
            ones = ones ^ num & ~twos;
            twos = twos ^ num & ~ones;
        }
        return ones;
    }
}

时间复杂度： $O (n)$ ，n位数组nums长度，每轮常数个位运算操作占用O(32*3*2)=O(1)。
空间复杂度： $O (1)$

2、遍历统计

思路：

求二进制位加总。
使用与运算，可获取二进制数字num的最右一位 $n_1$ ：
$n_1=num&i$
配合无符号右移操作，可获取num所有位的值（ $n_1$ ~ $n_{32}$ )
$n u m = n u m > > > 1$
建立32位数组counts，通过以上方法可记录所有数字的各二进制位的1出现次数。然后再对3求余，即可得到各个位的二进制结果。
恢复结果。
利用左移操作和或操作，可将counts数组各二进制的值恢复到数字res上。（循环区间[0-31]），最终返回res即可。

代码：

class Solution {
    public int singleNumber(int[] nums) {
        int[] counts = new int[32];
        // 1.二进制位加总
        for(int num : nums) {
            for(int j = 0; j < 32; j++) {
                counts[j] += num & 1;
                num >>>= 1;
            }
        }
        // 2. 恢复结果
        int res = 0, m = 3;
        for(int i = 0; i < 32; i++) {
            res <<= 1;
            res |= counts[31 - i] % m;
        }
        return res;
    }
}