向量胶囊的前向计算
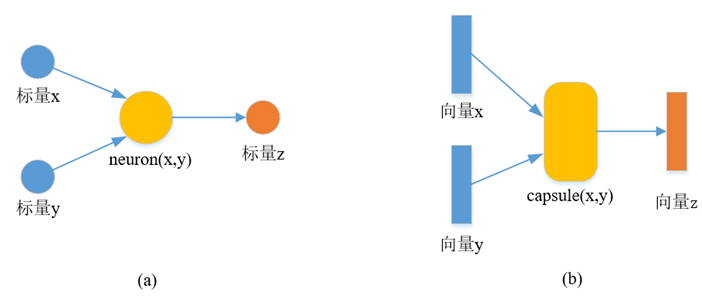
神经元用于检测一种确定的特征,而胶囊在检测特征的同时更注重描述这个特征。向量胶囊使用单位向量表达某种具体的特征,向量的模长反映该特征存在的概率。神经元与胶囊元的示意如图所示,(a)是神经元的计算演示,neuron是一个带有可学习参数的非线性变换,用于激活神经元得到输出结果。(b)是胶囊元的计算演示,capsule是一个带有可学习参数的非线性变换,与neuron的不同在于输入输出从标量变成向量。神经元的激活只能反映该特征存在的概率,忽略了同类特征之间的差异性,是不变性的体现;而胶囊包含了区分同类特征的信息,是等变性的体现,胶囊的模长为特征存在的概率,也是不变性的体现。
假设有两个输入向量,对于一个胶囊元capsule,应当输出一个向量,其前向计算过程如下图,
W
1
W_{1}
W1和
W
2
W_{2}
W2是转换矩阵,用于变换胶囊对象的基空间,故又称视觉不变矩阵。系数
c
1
c_{1}
c1和
c
2
c_{2}
c2称为耦合系数,其目的是实现传统神经网络中的池化过程(pooling),pooling可以视为一种固定的注意力,而耦合系数则增加了动态性,并且是不借助反向传播学习的注意力。转换矩阵通过反向传播计算梯度并更新得到,耦合系数则是利用动态路由进行更新。Squash函数用于压缩向量的大小但不改变方向,使其模长在0到1之间。
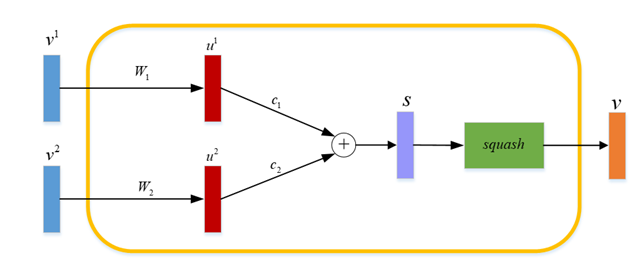
以图中的前向计算为例,假设动态路由迭代次数为
T
T
T,胶囊的动态路由更新过程描述如下:
步骤1. 将输入胶囊投影到视觉不变空间: u 1 = v 1 W 1 , u 2 = v 2 W 2 u^{1}=v^{1}W_{1},u^{2}=v^{2}W_{2} u1=v1W1,u2=v2W2,以及初始化系数 ( b 1 0 = 0 , b 2 0 = 0 ) (b_{1}^{0}=0,b_{2}^{0}=0) (b10=0,b20=0);
步骤2. 对于迭代的第 r r r次,执行以下操作:
-
(a)更新耦合系数: c 1 r , c 2 r = s o f t m a x ( b 1 r , b 2 r ) c_{1}^{r},c_{2}^{r}=softmax(b_{1}^{r},b_{2}^{r}) c1r,c2r=softmax(b1r,b2r)比如, c 1 0 , c 2 0 = s o f t m a x ( b 1 0 , b 2 0 ) = 0.5 c_{1}^{0},c_{2}^{0}=softmax(b_{1}^{0},b_{2}^{0})=0.5 c10,c20=softmax(b10,b20)=0.5;
-
(b)临时的聚合胶囊为: s r = c 1 r u 1 + c 2 r u 2 s^{r}=c_{1}^{r}u^{1}+c_{2}^{r}u^{2} sr=c1ru1+c2ru2
-
(c)对聚合胶囊的向量进行压缩: a r = s q u a s h ( s r ) = ∣ ∣ s r ∣ ∣ 2 1 + ∣ ∣ s r ∣ ∣ 2 ⋅ s r ∣ ∣ s r ∣ ∣ a^{r}=squash(s^{r})=frac{||s^{r}||^{2}}{1+||s^{r}||^{2}}cdotfrac{s^{r}}{||s^{r}||} ar=squash(sr)=1+∣∣sr∣∣2∣∣sr∣∣2⋅∣∣sr∣∣sr其中,当 ∣ ∣ s r ∣ ∣ ||s^{r}|| ∣∣sr∣∣的值较大时, ∣ ∣ s r ∣ ∣ 2 1 + ∣ ∣ s r ∣ ∣ 2 frac{||s^{r}||^{2}}{1+||s^{r}||^{2}} 1+∣∣sr∣∣2∣∣sr∣∣2将会趋近数值1,当 ∣ ∣ s r ∣ ∣ ||s^{r}|| ∣∣sr∣∣的值较小时, ∣ ∣ s r ∣ ∣ 2 1 + ∣ ∣ s r ∣ ∣ 2 frac{||s^{r}||^{2}}{1+||s^{r}||^{2}} 1+∣∣sr∣∣2∣∣sr∣∣2将会趋近数值0;
-
(d)更新系数: b i r = b i r − 1 + ( a r ) T u i , i ∈ { 1 , 2 } b_{i}^{r}=b_{i}^{r-1}+(a^{r})^{T}u^{i},iinleft{1,2right} bir=bir−1+(ar)Tui,i∈{1,2}
-
(e)更新迭代数 r = r + 1 r=r+1 r=r+1,如果 r = T r=T r=T,则将 a T − 1 a^{T-1} aT−1作为输出的聚合胶囊;否则,返回(a)并依次执行操作。
从动态路由更新的操作(d)可以看出,每次迭代都利用聚合胶囊与输入的视觉不变胶囊依次点积计算相似度,随着迭代过程的推进,耦合系数的分布将会发挥聚类作用,与聚合胶囊相似的胶囊将为结果提供更大比例的信息。这体现了耦合系数的动态变化注意力特点,它使得与数据加权中心相近的对象具有更高权重。
在梯度计算时,将迭代过程展开,计算形式和循环神经网络一致,因此,可以使用时序反向传播算法(BPTT,Back Propagation Through Time)更新可学习参数,即转换矩阵。
损失函数
向量胶囊网络基于折页函数构建损失。考虑图像识别问题,对于一个样本,假设类别数为 K K K,网络输出 K K K个胶囊向量,记 v k v_{k} vk为第 k k k个胶囊向量,该类别的损失计算为: L k = T k m a x ( 0 , m + − ∣ ∣ v k ∣ ∣ ) 2 + λ ( 1 − T k ) m a x ( 0 , ∣ ∣ v k − m − ∣ ∣ ) 2 L_{k}=T_{k}max(0,m^{+}-||v_{k}||)^{2}+lambda(1-T_{k})max(0,||v_{k}-m^{-}||)^{2} Lk=Tkmax(0,m+−∣∣vk∣∣)2+λ(1−Tk)max(0,∣∣vk−m−∣∣)2其中,如果第 k k k类是正确类别,则 T k = 1 T_{k}=1 Tk=1。 m + m^{+} m+和 m − m^{-} m−分别取值0.9,0.1,用于限制边界,一方面强迫模型加大分类置信度的差异,另一方面削弱超参数对模型性能的敏感性。 λ lambda λ取值0.5,用于平衡正确类别与错误类别之间的数值大小。该样本的损失为 K K K个类别对应的损失求和。
全连接向量胶囊网络
类比神经元组成神经网络的方法,我们可以将胶囊元组成胶囊网络,和神经元一样,每一个胶囊元都是为了检测一个特征,胶囊元输出胶囊的模长反映了该特征被激活的程度。胶囊本身则包含了该特征的描述信息,比如方向,旋转角度等。向量胶囊的全连接网络架构由卷积神经网络层,预胶囊层与全连接胶囊层构成,网络结构如图所示。
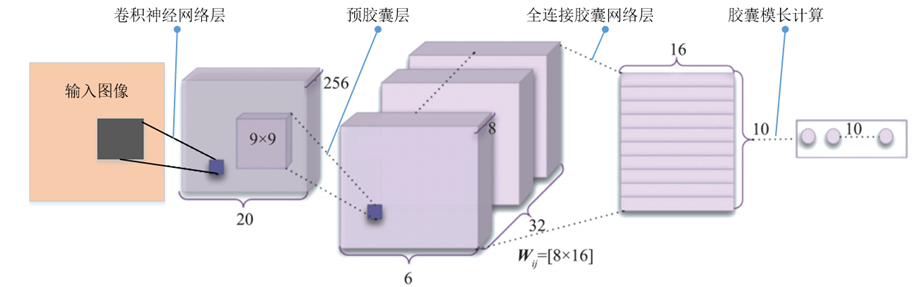
我们将图像输入标准的卷积神经网络CNN,通过CNN提取低层特征(颜色,边缘细节信息)。预胶囊层用于将低层特征转为胶囊形式,图中的预胶囊层是32个并行排列的CNN,得到32个尺寸为
6
×
6
6times 6
6×6的8通道特征图,对特征图变形得到
6
×
6
×
32
6times 6times 32
6×6×32个胶囊向量,,每个胶囊向量包含8个描述元素。这一变形操作是合理的,特征图的每个通道代表一个特征,8个通道代表胶囊向量包含的8个特征,即胶囊向量的描述元素。使用全连接的胶囊网络对
6
×
6
×
32
6times 6times 32
6×6×32个胶囊进行计算,输出10个具有高层语义的胶囊向量,每个胶囊向量包含16个描述元素,该层的可学习参数为转换矩阵
W
i
j
∈
R
8
×
16
W_{ij}in R^{8times 16}
Wij∈R8×16。
胶囊网络也可以迁移到卷积架构,我们只需将CNN的滤波器用胶囊网络进行替换。胶囊卷积网络可以实现局部胶囊信息的聚合,使用一组轻量级的胶囊网络作为滤波器在低层胶囊上卷积,在卷积核大小的区域中激活并反映出存在的高层语义胶囊。形象地描述,在张量的视角下,CNN生成特征图的每个像素都将用向量替换;与CNN同理,特征图的每一层“胶囊图”都代表一种特征,而“胶囊图”内每个胶囊的模长则反映该位置存在这个特征的概率。
最后
以上就是炙热白云最近收集整理的关于第三十课.向量胶囊与动态路由向量胶囊的前向计算损失函数全连接向量胶囊网络的全部内容,更多相关第三十课.向量胶囊与动态路由向量胶囊内容请搜索靠谱客的其他文章。



![[经典论文分享]CommNet 多智能体通讯网络模型](https://www.shuijiaxian.com/files_image/reation/bcimg14.png)




发表评论 取消回复