1 LRU Cache
1.1 特点

1.2 工作原理
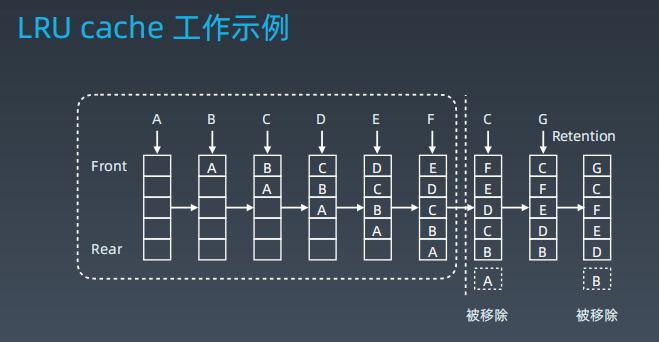
1.3 替换策略
1.4 模板
/**
* 哈希表 + 双向链表:一个哈希表和一个双向链表维护所有在缓存中的键值对
*
* 双向链表按照被使用的顺序存储了这些键值对,靠近头部的键值对是最近使用的,而靠近尾部的键值对是最久未使用的。
* 哈希表即为普通的哈希映射(HashMap),通过缓存数据的键映射到其在双向链表中的位置。
*
* 思路:
* 1.用字典来存储 key-value 结构,这样对于查找操作时间复杂度就是 O(1);
* 2.但是因为字典本身是无序的,所以我们还需要一个类似于队列的结构来记录访问的先后顺序。需要支持如下几种操作:在末尾加入一项、去除最前端一项、将队列中某一项移到末尾;
* 3.首先考虑列表结构,但是列表无法在常数时间内把某个value挑出来移到队尾;
* 4.再考虑单链表,可以在常数的时间内找到对应的节点,但是如果想将它移到尾部则需要从头遍历到该节点才能保证链表不断,时间复杂度也是O(n);
* 5.双链表,解决了移到末尾这个问题;
*
* @constructor Create empty L r u cache
*/
class LRUCache(capacity: Int) {
internal class LinkedNode(var key: Int, var `val`: Int) {
var pre: LinkedNode? = null
var next: LinkedNode? = null
}
/**
* 总容量
*/
private var capacity: Int
/**
* 当前容量
*/
private var size: Int = 0
/**
* 使用伪头部和伪尾部节点
*/
private var head = LinkedNode(0, 0)
private var tail = LinkedNode(0, 0)
/**
* 哈希表快速定位节点
*/
private val cache: MutableMap<Int, LinkedNode> = mutableMapOf()
init {
this.capacity = capacity
head.next = tail
tail.pre = head
}
/**
* operator允许cache[1]获取
*
* @param key
* @return
*/
operator fun get(key: Int): Int {
val node = cache[key] ?: return -1
// 如果 key 存在,先通过哈希表定位,再移到头部
moveToHead(node)
return node.`val`
}
/**
* 添加key-value
*
* @param key
* @param val
*/
fun put(key: Int, `val`: Int) {
val node = cache[key]
if (node == null) {
// 如果 key 不存在,创建一个新的节点
val newNode = LinkedNode(key, `val`)
// 添加进哈希表
cache[key] = newNode
// 添加至双向链表的头部
addToHead(newNode)
if (size > capacity) {
// 如果超出容量,删除双向链表的尾部节点
val tail = removeTail()
// 删除哈希表中对应的项
cache.remove(tail.key)
}
} else {
// 如果 key 存在,先通过哈希表定位,再修改 `val`,并移到头部
node.`val` = `val`
moveToHead(node)
}
}
/**
* 添加至双向链表的头部
*
* @param node
*/
private fun addToHead(node: LinkedNode) {
// 处理右指向
node.next = head.next
head.next?.pre = node
// 处理左指向
node.pre = head
head.next = node
size++
}
/**
* 移动到双向链表的头部
*
* @param node
*/
private fun moveToHead(node: LinkedNode) {
removeNode(node)
addToHead(node)
}
/**
* 删除双向链表的尾部节点
*
* @return
*/
private fun removeTail(): LinkedNode {
val node: LinkedNode = tail.pre!!
removeNode(node)
return node
}
/**
* 删除双向链表的当前节点
*
* @param node
*/
private fun removeNode(node: LinkedNode) {
node.pre?.next = node.next
node.next?.pre = node.pre
size--
}
}
2 布隆过滤器(Bloom Filter)
2.1 特点
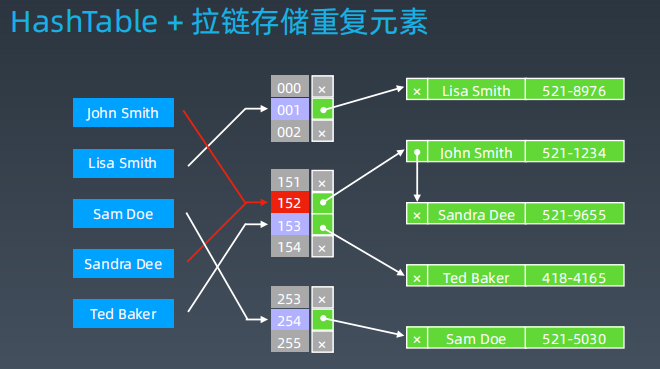
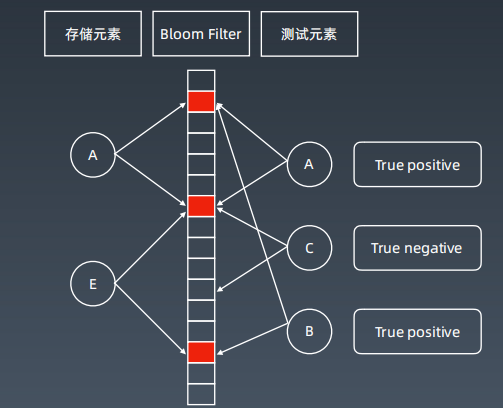
2.2 对比哈希表

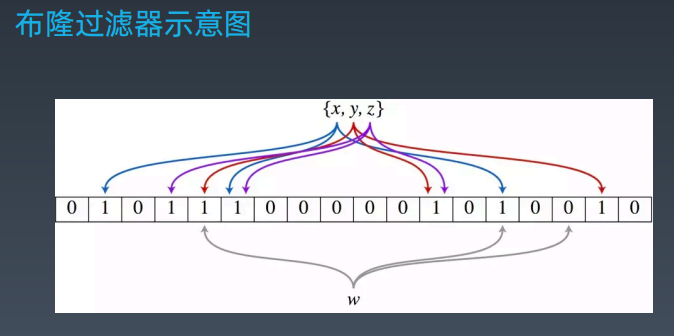
2.3 案例

最后
以上就是迷人小蝴蝶最近收集整理的关于算法刻意练习之布隆过滤器/LRU Cache的全部内容,更多相关算法刻意练习之布隆过滤器/LRU内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复