布隆过滤器
需求
如果需要编写一个网络爬虫,去爬10亿个网站数据,为了避免爬到重复的网站,如何判断某个网站是否爬过?
首先,10亿个网站数据量很大,使用哈希表有些不合适。
哈希表确实可以做到O(1)级别找到对应的元素,但10亿级别的数据量,空间复杂度太大,就不合适了。因此,我们需要尝试使用新思路、新方法:布隆过滤器。
set之所以可以做到O(1)级别的查找某个元素是否存在,是因为其底部使用的是Hash表,而hash表底层是使用的数组。
hashMap之所以可以做到O(1)级别的查找某个元素的对应元素,是因为其底部使用的是Hash表,而hash表底层是使用的数组。
布隆过滤器(Bloom Filter)
问:布隆过滤器是解决什么问题?
判断某一元素是否存在,且时间复杂度低、空间复杂度低。
布隆过滤器是在1970年,由布隆提出的。
布隆过滤器是一个空间效率高的概率型数据结构,用来告诉你,一个元素一定不存在或可能存在。
优缺点:
优点:空间效率和查询时间都远远超过一般的算法
缺点:有一定的误判率、删除困难
它实际上是一个很长的二进制向量和一系列随机映射函数(Hash函数)
二进制向量可以理解为二进制数组
在实现的时候可以使用long类型的数组。每个long64个字节
常见应用:
网页黑名单系统、垃圾邮件过滤系统、爬虫网址判重系统、解决缓存穿透问题
布隆过滤器原理
假设布隆过滤器由20位二进制、3个哈希函数组成,每个元素经过哈希函数处理都能生成一个索引位置。
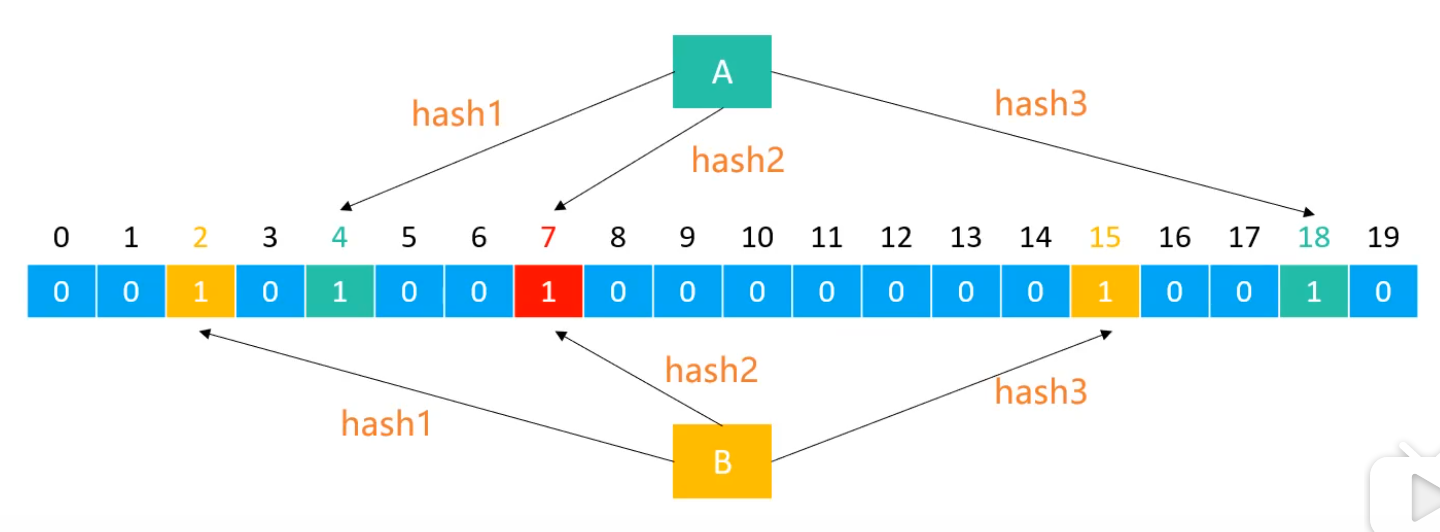
添加元素:将每一个哈希函数生成的索引位置都设置为1
查询元素是否存在
如果有一个哈希函数生成的索引位置不为1,就代表不存在(100%准确)
如果每一个哈希函数生成的索引位置都为1,就代表存在(存在一定的误判率)
添加、查询的时间复杂度都是O(k),k是哈希函数的个数。
添加、查询的空间复杂度都是O(m),m是二进制位的个数。
布隆过滤器的误判率
误判率p受3个因素影响:
二进制位的个数m
哈希函数的个数k
数据规模m

跳表
问:一个有序链表的搜索、添加、删除的平均时间复杂度是多少?
答:O(n)
搜索需要遍历,添加、删除也需要遍历。既然需要遍历,平均时间复杂度就是O(n)
对于有序数组,我们知道,可以使用二分搜索的方法,使得数组的搜索的平均时间复杂度为O(logn)
题外话:
想知道无序数组的查找、添加、删除的时间复杂度
有序数组使用二分查找的查找、添加、删除的时间复杂度
查了一些资料,发现百度推的头两篇文章给出的答案是:
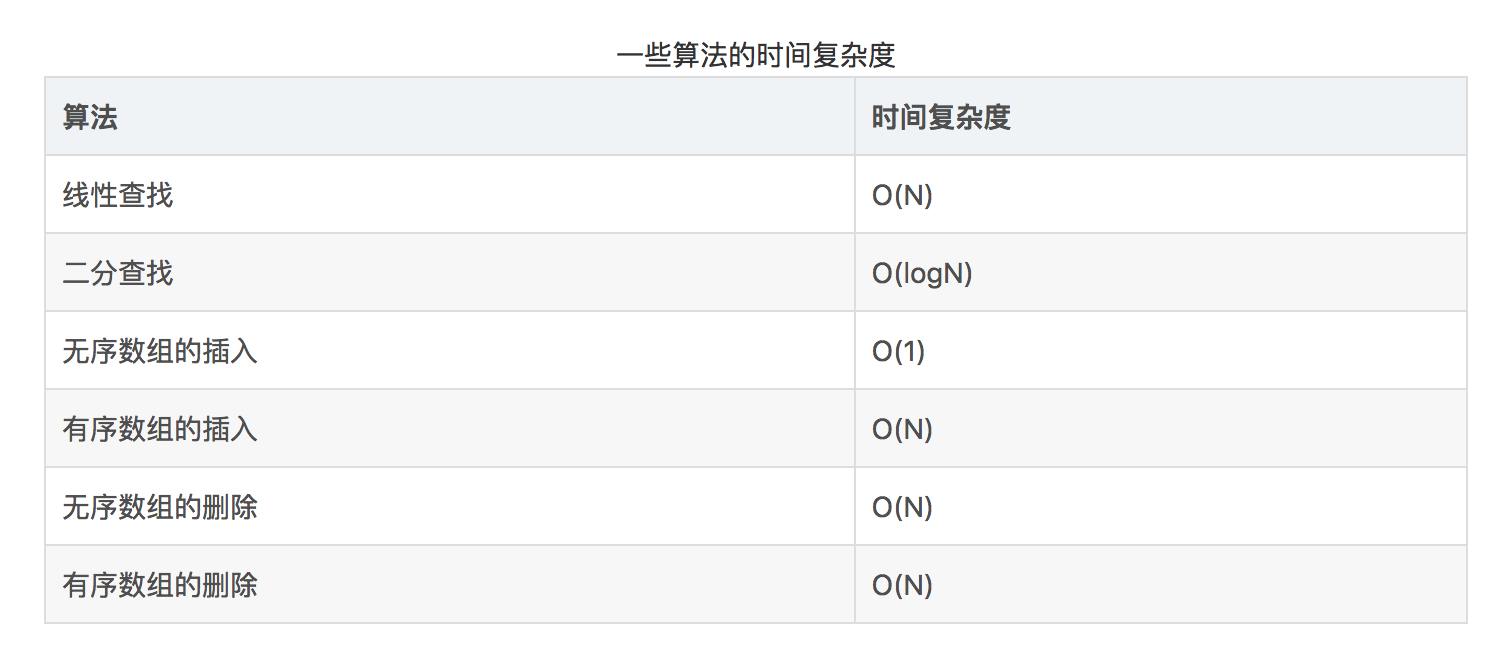
这答案,我觉得不严谨
作者是否想说的是平均时间复杂度?
即使时间复杂度代表的是平均时间复杂度,那么无序数组的插入平均复杂度也不是O(1),而是O(n)
翻了下手头的书,给出一份自己的答案:
| 复杂度分析 | 最好时间复杂 | 最坏时间复杂度 | 平均时间复杂度 |
|---|---|---|---|
| 线性查找 | O(1) | O(n) | O(n) |
| 二分查找 | O(1) | O(logn) | O(logn) |
| 无序数组的插入 | O(1) | O(n) | O(n) |
| 有序数组的插入 | O(1) | O(n) | O(n) |
| 无序数组的删除 | O(1) | O(n) | O(n) |
| 有序数组的删除 | O(1) | O(n) | O(n) |
查找分为两种:
- 查找数组某一位置的元素值
- 查找数组中是否存在某一元素
如果是查找数组某一位置的元素值,那么查找的最好、最坏、平均时间复杂度为O(1)
如果是查找数组中是否存在某一元素,那么查找的最好、最坏、平均时间复杂度为上述表中的内容。(分为线性查找、二分查找)
那么,能否利用二分搜索优化一下有序链表,使得搜索、添加、删除的平均时间复杂度降低为O(logn)?
不可以,之所以有序数组可以使用二分查找,是因为array[i]这步操作
而list->data,没有直接取,只能list->next->next一步一步找到第i个元素值。因此,无法使用二分查找。
换句话说就是:链表没有像数组那样的高效随机访问(O(1)时间复杂度),所以不能像有序数组那样直接进行二分搜索优化
问:有没有其他办法,使得有序链表的搜索、插入、删除的平均复杂度降低为O(logn)?
这就是我们接下来要学习的:跳表(SkipList)
跳表,又称为跳跃表、跳跃列表,其是在有序链表的基础上增加了“跳跃”的功能。
设计的初衷是取代平衡树(比如红黑树)
对比平衡树
跳表的实现和维护会更加简单
跳表的搜索、插入、删除的平均时间复杂度为O(logn)
使用跳表优化链表
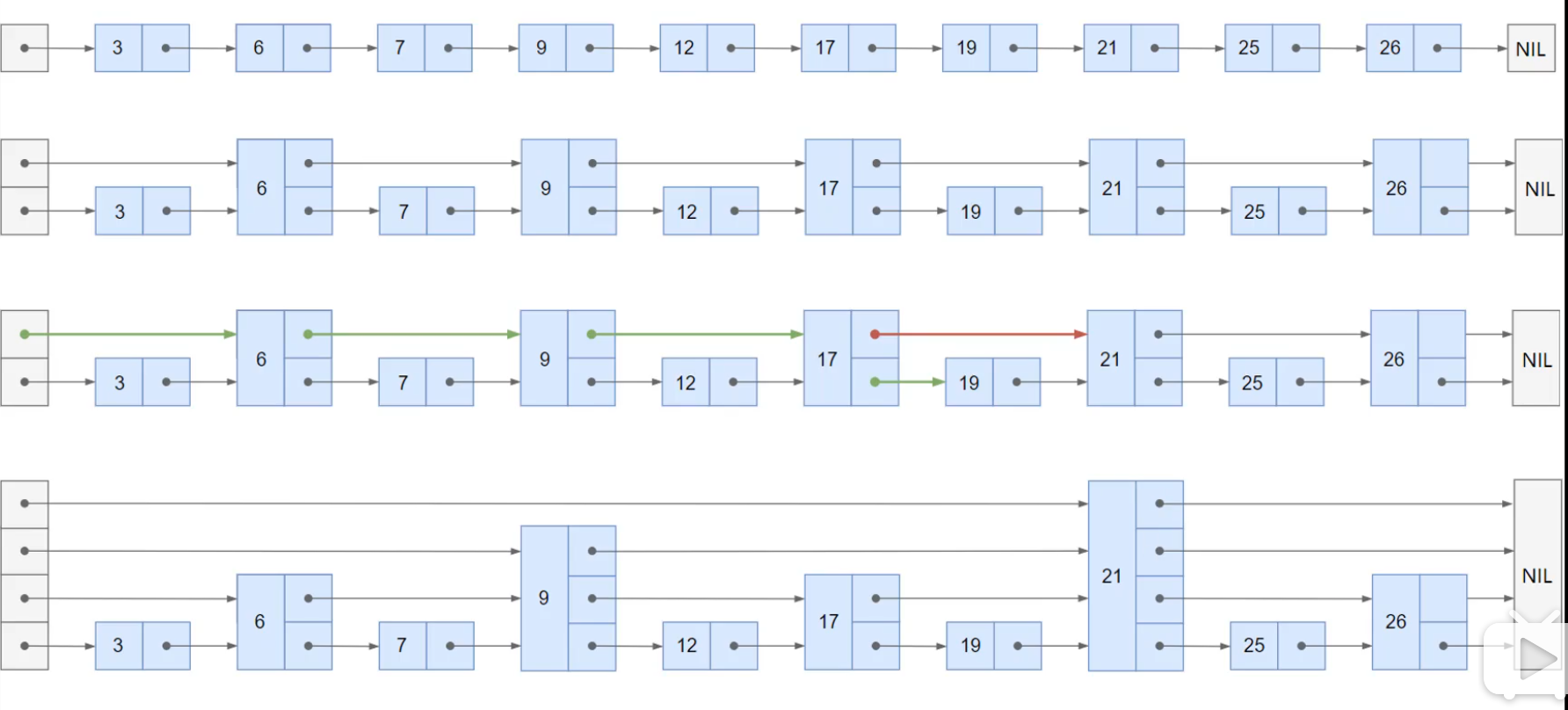
跳表的搜索:
- 从顶层链表的首元素开始,从左往右搜索,直至找到一个大于或者等于目标的元素,或者到达当前层链表的尾部
- 如果该元素等于目标,则表明该元素已被找到
- 如果该元素大于目标元素或者已到达链表的尾部,则退回到当前层的前一个元素,然后转入下一层进行搜索。
举个例子:
假如要找19
第一种方法需要一个一个遍历
第二种方法,可以一个跳一个,找到21,比19大,返回至17,往下走,再往前19被找到
…
第四种方法,一下找到21,比19大,返回。往下走,找到9,继续走,21比19大,返回9。往下走,17比20小,继续往前21,返回17,往下走,继续往前,19,找到。
跳表,是针对有序链表,链表的组成包括data和next
既然是有序,就需要有比较性。data其实是一个key-value类型。key作为比较,value用来存值。
上述查找19,其实就是查找key为19。至于19里面的元素是什么,没有体现。
private static class Node<K, V>
{
K key;
V value;
Node<K, V>[] nexts;//由于每个结点的next个数不一样,可以使用数组
}
一般首节点的nexts最大长度为32。
一般来说,nexts应该是实际链表结点中,某个拥有nexts最多的就是头结点的nexts数,比如上面的图,nexts = 4,是21的地方,nexts为4。
但在初始化的时候,由于不知道实际结点的nests数,因此,我们将头结点的nexts长度设定为32
跳表的添加、删除

假如添加的是17
17是多少层呢?也就是17的nexts数组长度是多少?
这是一个概率问题,类似抛硬币,正面+1,负数结束。
确定完层数后,将6的第四层指针指向17、6的第三层指针指向17、9的第二层指针指向17、12的第一层指针指向17。
假如是删除17
将原来执行17的指针,执行同层17执行的指针即可。
最后
以上就是健壮溪流最近收集整理的关于数据结构与算法---布隆过滤器、跳表布隆过滤器布隆过滤器(Bloom Filter)跳表的全部内容,更多相关数据结构与算法---布隆过滤器、跳表布隆过滤器布隆过滤器(Bloom内容请搜索靠谱客的其他文章。








发表评论 取消回复