目录

为什么要有布隆过滤器

简介

基本原理

是否支持删除

误判率

哈希函数个数和布隆过滤器长度

复杂度

空间

时间

优缺点

优点

缺点

BloomFilter和BItMap的区别

应用

java实现

Hash工具类

BitSet类

BloomFilter

测试

Counting Bloom Filter

Spectral Bloom Filter

---

为什么要有布隆过滤器

在日常生活中，包括在设计计算机软件时，我们经常要判断一个元素是否在一个集合中。比如在字处理软件中，需要检查一个英语单词是否拼写正确（也就是要判断 它是否在已知的字典中）；在 FBI，一个嫌疑人的名字是否已经在嫌疑名单上；在网络爬虫里，一个网址是否被访问过等等。最直接的方法就是将集合中全部的元素存在计算机中，遇到一个新 元素时，将它和集合中的元素直接比较即可。一般来讲，计算机中的集合是用哈希表（hash table）来存储的。它的好处是快速准确，缺点是费存储空间。当集合比较小时，这个问题不显著，但是当集合巨大时，哈希表存储效率低的问题就显现出来 了。比如说，一个象 Yahoo,Hotmail 和 Gmai 那样的公众电子邮件（email）提供商，总是需要过滤来自发送垃圾邮件的人（spamer）的垃圾邮件。一个办法就是记录下那些发垃圾邮件的 email 地址。由于那些发送者不停地在注册新的地址，全世界少说也有几十亿个发垃圾邮件的地址，将他们都存起来则需要大量的网络服务器。如果用哈希表，每存储一亿 个 email 地址， 就需要 1.6GB 的内存（用哈希表实现的具体办法是将每一个 email 地址对应成一个八字节的信息指纹， 然后将这些信息指纹存入哈希表，由于哈希表的存储效率一般只有 50%，因此一个 email 地址需要占用十六个字节。一亿个地址大约要 1.6GB， 即十六亿字节的内存）。因此存贮几十亿个邮件地址可能需要上百 GB 的内存。除非是超级计算机，一般服务器是无法存储的。

简介

本质上布隆过滤器是一种数据结构，比较巧妙的概率型数据结构（probabilistic data structure），特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”。

相比于传统的 List、Set、Map 等数据结构，它更高效、占用空间更少，但是缺点是其返回的结果是概率性的，而不是确切的。

布隆过滤器是一种多哈希函数映射的快速查找算法。它可以判断出某个元素肯定不在集合里或者可能在集合里，即它不会漏报，但可能会误报。通常应用在一些需要快速判断某个元素是否属于集合，但不严格要求100％正确的场合。

基本原理

布隆过滤器是一个 bit 向量或者说 bit 数组，长这样：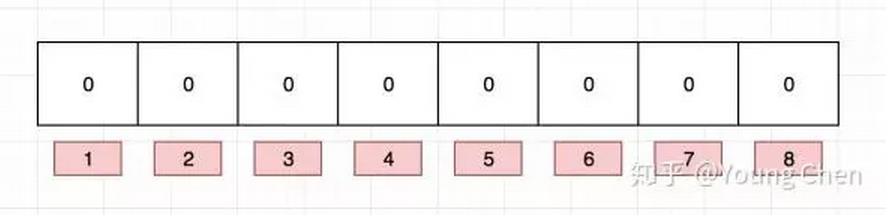

如果我们要映射一个值到布隆过滤器中，我们需要使用多个不同的哈希函数生成多个哈希值，并对每个生成的哈希值指向的 bit 位置 1，例如针对值 “baidu” 和三个不同的哈希函数分别生成了哈希值 1、4、7，则上图转变为：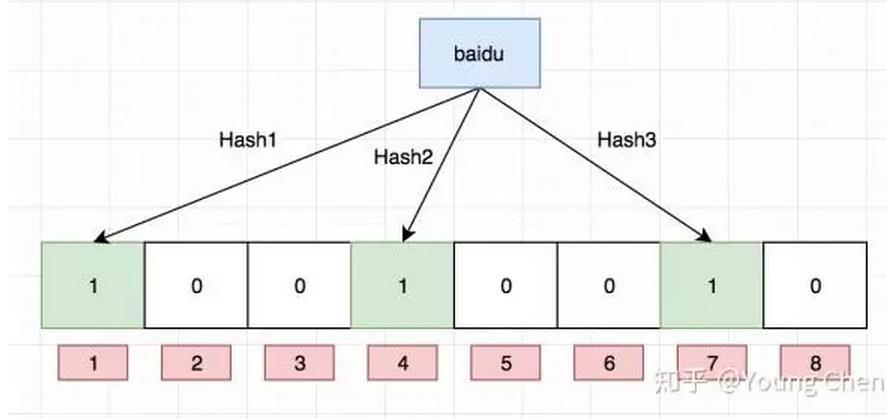

Ok，我们现在再存一个值 “tencent”，如果哈希函数返回 3、4、8 的话，图继续变为：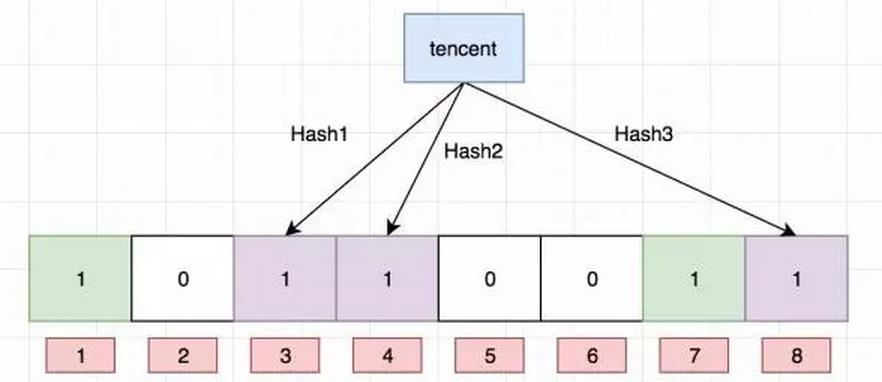

值得注意的是，4 这个 bit 位由于两个值的哈希函数都返回了这个 bit 位，因此它被覆盖了。现在我们如果想查询 “dianping” 这个值是否存在，哈希函数返回了 1、5、8三个值，结果我们发现 5 这个 bit 位上的值为 0，说明没有任何一个值映射到这个 bit 位上，因此我们可以很确定地说 “dianping” 这个值不存在。而当我们需要查询 “baidu” 这个值是否存在的话，那么哈希函数必然会返回 1、4、7，然后我们检查发现这三个 bit 位上的值均为 1，那么我们可以说 “baidu” 存在了么？答案是不可以，只能是 “baidu” 这个值可能存在。

这是为什么呢？答案跟简单，因为随着增加的值越来越多，被置为 1 的 bit 位也会越来越多，这样某个值 “taobao” 即使没有被存储过，但是万一哈希函数返回的三个 bit 位都被其他值置位了 1 ，那么程序还是会判断 “taobao” 这个值存在。

是否支持删除

目前我们知道布隆过滤器可以支持 add 和 isExist 操作，那么 delete 操作可以么，答案是不可以，例如上图中的 bit 位 4 被两个值共同覆盖的话，一旦你删除其中一个值例如 “tencent” 而将其置位 0，那么下次判断另一个值例如 “baidu” 是否存在的话，会直接返回 false，而实际上你并没有删除它。

如何解决这个问题，答案是计数删除。但是计数删除需要存储一个数值，而不是原先的 bit 位，会增大占用的内存大小。这样的话，增加一个值就是将对应索引槽上存储的值加一（即存储的不是0,1，而是0,1,2,3，。。。），删除则是减一，判断是否存在则是看值是否大于0。

误判率

误判率就是在插入n个元素后，某元素被判断为“可能在集合里”，但实际不在集合里的概率，此时这个元素哈希之后的k个比特位置都被置为1。

假设哈希函数等概率地选择每个数组位置，即哈希后的值符合均匀分布，那么每个元素等概率地哈希到位数组的m个比特位上，与其他元素被哈希到哪些位置无关(独立事件)。设定数组总共有m个比特位，有k个哈希函数。在插入一个元素时，一个特定比特没有被某个哈希函数置为1的概率是：

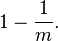
插入一个元素后，这个比特没有被任意哈希函数置为1的概率是：

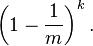
在插入了n个元素后，这个特定比特仍然为0的概率是：

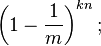
所以这个比特被置为1的概率是：

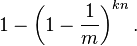
现在检测一个不在集合里的元素。经过哈希之后的这k个数组位置任意一个位置都是1的概率如上。这k个位置都为1的概率是：

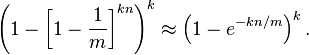
哈希函数个数和布隆过滤器长度

对于给定的m和n，让“误报率”最小的k值为：

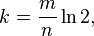
此时“误报率”为：

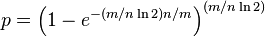
可以简化为：

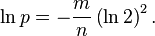
上面的公式，可以看到，设定一个误判率p，可以得到m=x*n  得到x，就可以得到k

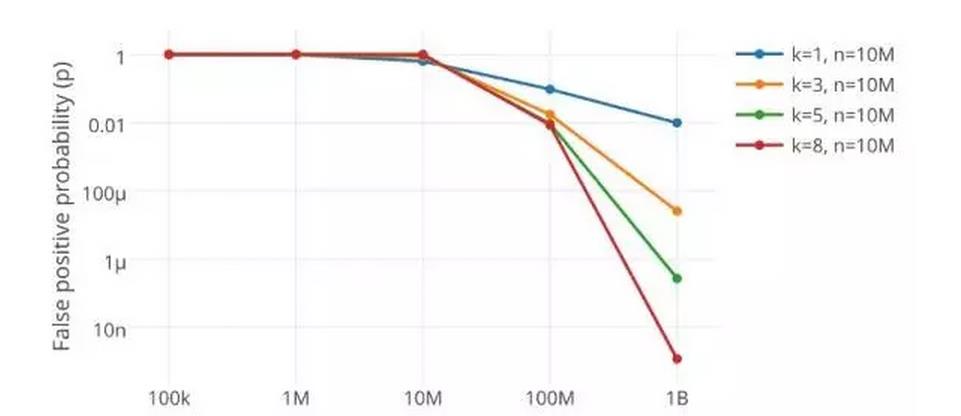
在leveldb中，设定的误判率<=1%,所以m/n是9.6，即10个比特，此时k=6.72，即7bit，即需要7次hash，每个元素占7bit，总共需要m=n*9.6个比特作为布隆过滤器的位数组数据。

结果是对于误报率<=1%,对于插入n个元素，要有7个哈希函数，9.6*n 个比特作为布隆过滤器的长度

复杂度

空间

空间就是布隆过滤器的长度m，可以看到最优长度m=x*n，插入n个数，空间复杂度为O(n)

时间

进行一次哈希操作时间是常数时间，每插入一个数，要执行k次哈希运算和k次置1，还是常数时间

插入n个数，时间复杂度为O(n)

检验一个数在不在布隆过滤器中，时间为常数时间O(C)

优缺点

优点

1. 存储空间和插入/查询时间都是常数，远远超过一般的算法
2. Hash函数相互之间没有关系，方便由硬件并行实现
3. 不需要存储元素本身，在某些对保密要求非常严格的场合有优势

缺点

1. 有一定的误识别率
2. 删除困难

BloomFilter和BItMap的区别

其实主要的区别在于两者，一个value对应位图的位置不同

bitmap，是一一对应，保证一个value对应一个格，所以只需对应一格，还十分准确

BloomFilter 是hashcode，不能保证一个value对应一格，所以要有多个hash函数，还有失误率，而且还不能删除，但是BloomFilter节省了空间，还能面对string这种肯定不能一一对应的场景

 

应用

搜索引擎中的海量网页去重

leveldb等数据库中快速判断元素是否存在，可以显著减少磁盘访问

Google 著名的分布式数据库 Bigtable 使用了布隆过滤器来查找不存在的行或列，以减少磁盘查找的IO次数。

Squid 网页代理缓存服务器在 cache digests 中使用了也布隆过滤器。

Venti 文档存储系统也采用布隆过滤器来检测先前存储的数据。

SPIN 模型检测器也使用布隆过滤器在大规模验证问题时跟踪可达状态空间。

Google Chrome浏览器使用了布隆过滤器加速安全浏览服务。

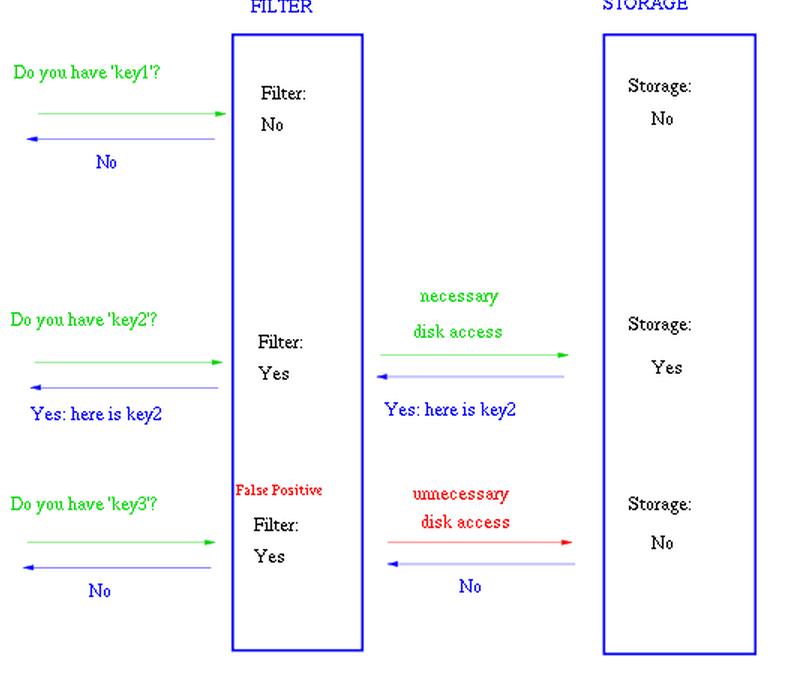
在很多Key-Value系统中也使用了布隆过滤器来加快查询过程，如 Hbase，Accumulo，Leveldb，一般而言，Value 保存在磁盘中，访问磁盘需要花费大量时间，然而使用布隆过滤器可以快速判断某个Key对应的Value是否存在，因此可以避免很多不必要的磁盘IO操作，只是引入布隆过滤器会带来一定的内存消耗，下图是在Key-Value系统中布隆过滤器的典型使用：

java实现

Hash工具类

这里的hash函数与string的那个hashcode方法基本一样，就是将31换成seed，最后mod maxLength，保证bitSet的范围

package algorithm.find.bloomfilter;

/**BloomFilter的hash工具类，用来对对应的value生成hashcode
 *
 */
public class BloomHash {
	
	/**
	 * Hash工具类返回的hashcode的最大长度<br>
	 * maxLength为2的n次方，返回的hashcode为[0,2^n-1]
	 */
	public int maxLength;
	
	/**
	 * Hash函数生成哈希码的关键字
	 */
	public int seed;

	public BloomHash(int maxLength, int seed) {
		this.maxLength = maxLength;
		this.seed = seed;
	}
	
	/**返回字符串string的hashcode，大小为[0,maxLength-1]
	 * @param string
	 * @return
	 */
	public int hashCode(String string){
		int result=0;
		//这个构建hashcode的方式类似于java的string的hashcode方法
		//只是我这里是可以设置的seed，它那里是31
		for(int i=0;i<string.length();i++){
			result=result+seed*string.charAt(i);
		}
		//maxLength-1=111111,相当于result mod (maxLength-1)  
		//保证结果在[0,maxLength-1]
		return (maxLength-1)&result;
	}
	
	

}

BitSet类

bloomfilter类对位图的操作基于java.util.BitSet  ，所以做个基本介绍它的api

BitSet的底层实现是使用long数组作为内部存储结构的，所以BitSet的大小为long类型大小(64位)的整数倍

BitSet(int nbits)：创建一个位set，它的初始大小足以显式表示索引范围在 0 到 nbits-1 的位

bitSet.set(index) 将index位 置1

bitSet.get(index)   将index位 返回

 

BloomFilter

注释很详细，总共7个hash函数，100万左右的bit位

对位图的操作基于上面的bitset

package algorithm.find.bloomfilter;

import java.util.BitSet;

public class BloomFilter {
	
	
	/**
	 * 构建hash函数的关键字，总共7个
	 */
	private static final int[] HashSeeds=new int[]{3,5,7,11,13,17,19}; 
	
	/**
	 * Hash工具类的数组
	 */
	private static BloomHash[] HashList=new BloomHash[HashSeeds.length];
	
	/**
	 * BloomFilter的长度，最好为插入数量的10倍，目前为2的20次方，大约100万个
	 */
	private static final int BloomLength=1<<20;
	
	/**
	 * 对位的操作类，java自带的BitSet，共BloomLength个bit
	 */
	private BitSet bitSet=new BitSet(BloomLength);
	
	
	public BloomFilter(){
		//初始化Hash工具类的数组,每个hash工具类的hash函数都不同
		for(int i=0;i<HashSeeds.length;i++){
			HashList[i]=new BloomHash(BloomLength, HashSeeds[i]);
		}
	}
	
	/**在布隆过滤器中加入值value，在多个hash函数生成的hashcode对应的位置上，置1
	 * @param value 字符串，如果为数字，可以自己转化成string
	 */
	public void addValue(String value){
		for(int i=0;i<HashSeeds.length;i++){
			//根据对应的hash函数得到hashcode
			int hashcode=HashList[i].hashCode(value);
			//在位图中，将对应的位，设置为1
			bitSet.set(hashcode);
		}
	}
	
	/**在布隆过滤器中,检验是否可能有值value
	 * @param value
	 * @return 如果返回false，则一定没有<br> 如果返回true，就代表有可能有
	 */
	public boolean existsValue(String value){
		boolean result=true;
		for(int i=0;i<HashSeeds.length;i++){
			//根据对应的hash函数得到hashcode
			int hashcode=HashList[i].hashCode(value);
			//将result与对应位置上的0或1 做与运算
			//如果全为1，则result最后为1
			//如果有一个位置上为0，则最后result为0
			result=result&bitSet.get(hashcode);
		}		
		return result;
		
	}

	
	
	
}

测试

package algorithm.find.bloomfilter;

public class Main {

	public static void main(String[] args) {
		BloomFilter filter=new BloomFilter();
		filter.addValue("1234");
		System.out.println(filter.existsValue("1234"));
		System.out.println(filter.existsValue("12341"));
	}

}

Counting Bloom Filter

从前面对Bloom Filter的介绍可以看出，标准的Bloom Filter是一种很简单的数据结构，它只支持插入和查找两种操作。在所要表达的集合是静态集合的时候，标准Bloom Filter可以很好地工作，但是如果要表达的集合经常变动，标准Bloom Filter的弊端就显现出来了，因为它不支持删除操作。

Counting Bloom Filter的出现解决了这个问题，它将标准Bloom Filter位数组的每一位扩展为一个小的计数器（Counter），在插入元素时给对应的k（k为哈希函数个数）个Counter的值分别加1，删除元素时给对应的k个Counter的值分别减1。Counting Bloom Filter通过多占用几倍的存储空间的代价，给Bloom Filter增加了删除操作。下一个问题自然就是，到底要多占用几倍呢？

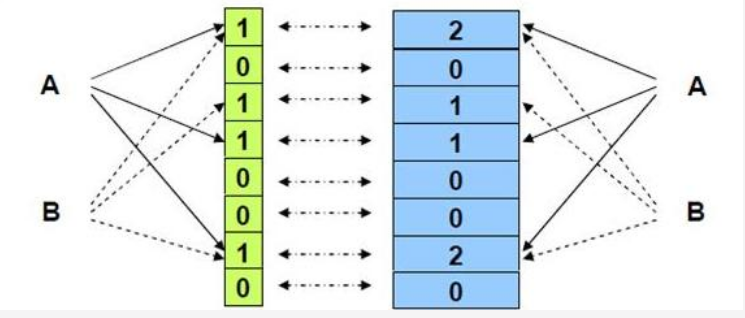
我们先计算第i个Counter被增加j次的概率，其中n为集合元素个数，k为哈希函数个数，m为Counter个数（对应着原来位数组的大小）：

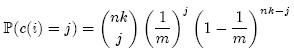
上面等式右端的表达式中，前一部分表示从nk次哈希中选择j次，中间部分表示j次哈希都选中了第i个Counter，后一部分表示其它nk – j次哈希都没有选中第i个Counter。因此，第i个Counter的值大于j的概率可以限定为：

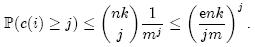
上式第二步缩放中应用了估计阶乘的斯特林公式：

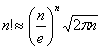
k的最优值为(ln2)m/n，现在我们限制k ≤ (ln2)m/n，就可以得到如下结论：

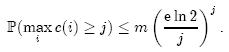
如果每个Counter分配4位，那么当Counter的值达到16时就会溢出。这个概率为：

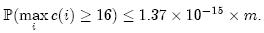
这个值足够小，因此对于大多数应用程序来说，4位就足够了。

Spectral Bloom Filter

Bloom filter将集合中的元素映射到位数组中，用k（k为哈希函数个数）个映射位是否全1表示元素在不在这个集合中。Counting bloom filter（CBF）将位数组中的每一位扩展为一个counter，从而支持了元素的删除操作。

一旦位扩展成了counter，每一个counter就不仅能表示这一地址有无映射，还能表示映射的个数。这一扩展使得存储的数据包含了更多信息，然而遗憾的是，CBF仅仅利用这个扩展支持了删除操作，并没有将信息中蕴含的潜力完全挖掘出来。毫无疑问，Spectral Bloom Filter（SBF）的提出者就看到了这种潜力。

标准的bloom filter和CBF解决的只是集合元素的membership问题，即判断一个元素是否属于某个集合。但有时我们不但想知道集合中是否存在一个元素，我们还想知道这个元素在集合中的出现次数。例如在一些数据流（data stream）应用中，我们关心的也许不是一个数据元素是否属于某个集合，而是它的出现频率。很自然地，我们希望能从counter中得到这些信息。但是，counter反映的只是映射数，如何将其与集合元素的出现次数关联呢？

在CBF中加入一个元素时，k个哈希位置的counter都要加1。也就是说，如果不考虑碰撞（collision），出现次数为n的元素对应的k个counter的值都为n。即使考虑到碰撞的因素，只要k个位置不全出现碰撞，k个counter中的最小值仍是n。令元素x对应的k个counter的最小值为mx，x的出现频率为fx，从上面的分析我们不难看出，fx ≠ mx的概率和标准bloom filter的false positive概率相同，因为二者出现的充要条件都是k个哈希位置同时出现碰撞。

上面这个结果其实就是SBF的理论基础。SBF扩展了CBF，使得用户不但可以进行membership query，还可以查询集合元素的出现频率。在查询元素x的出现频率时，SBF返回mx，出错的概率和false positive rate相同。注意，由于fx ≤ mx，所以查询的结果即使不准，也可以得到一个上界，而且这个上界和实际值fx一般情况下不会相差太远。

到现在为止讲的都是概念，我们还没有看到SBF和CBF在构造上有什么不同。当然，如果不改变CBF就可以加入新的feature，那最好不过了，可惜事情没有这么简单。CBF的counter在只支持membership query的时候，4位就够了，如果想要支持元素的出现频率查询，4位就远远不够。由于元素有可能成百上千次重复出现，而且完全没法预测，所以SBF的counter必须能够动态伸缩。

为实现counter的高效存储，我们先简化问题，来看最少需要多少位才能存储所有的counter。假设SBF要表示M个元素的集合（可能包含重复元素），counter数组的长度为m（对应着bloom filter的位数组），显然所有counter需要的最少位数N为

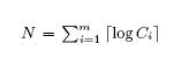
其中Ci表示counter数组中第i个counter的大小，即哈希函数映射到第i位的次数。用N位存储counter，其实相当于把所有的counter化成二进制位串然后连在一起。这样当然占用的位数最少，但如何访问长度不一的counter是个大问题。不管怎么样，在不考虑增删操作的情况下，我们想要达到的目标就是在保证查询操作快速的基础上，使得存储位数尽量接近N。

SBF并没有发明什么异乎寻常的高超技巧，和你大概能想到的一样，它构建了一套索引结构。首先SBF将N位的基本位串分成m/logN段，每一段包含logN个counter，然后将每一段的offset记下来。由于offset要占用logN位，所以记录子串offset的数组（论文中叫Coarse Vector）总长度为m位。

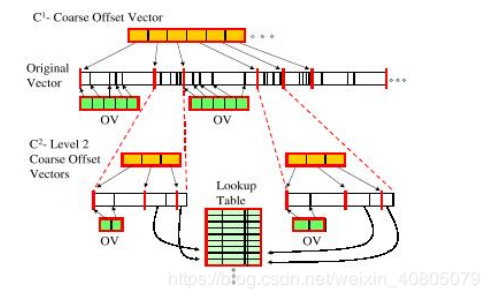
有了Coarse Vector，我们就可以随机访问任何一个子串了。这时我们有两种选择，要么把子串继续分成子段，要么将子串中所有counter的offset记下来（即上图中的OV，Offset Vector）。子串有长有短，但所含counter个数相同，也就是记录counter的offset数组长度相同，这就意味着把长子串用来记录offset比较划算。SBF规定子串长度超过log3N位的，直接用offset数组记录counter位置，否则再继续分。N位基本位串中最多有N/log3N个长度不超过log3N的子串，所以在这一层所有的offset数组加起来长度最多为N/log3N × (logN × logN) = N/logN位。

长度不超过log3N位的子串，我们将其再分成loglogN段，每一段包含logN/loglogN个counter。由于offset要占用loglog3N = 3loglogN位，所以整个offset数组总长度为3loglogN ×logN/loglogN = 3logN位。这一层所有的offset数组加起来长度最多为m/logN × 3logN ＝ 3m位。

并不是子串的每一个子段都用offset数组来存储counter的位置，和前面一样，仍然只记录较长的子段。假设子段长度为T，这里的阀值设为T0 = (loglogN)3，当T > T0时，子段的counter位置用offset数组记录。由于子段包含loglogN个counter，且每一个offset可以用3loglogN位表示，因此offset数组的长度最多为loglogN × 3loglogN ＝ 3(loglogN)2 « T。这一层的所有的offset数组长度加起来也不过O(N)。

现在就剩了T ≤ T0的情况，这时SBF也不继续分了，而是将所有这类情况存储在一个全局查询表里。关于这个查询表，这里就不多做介绍了，有兴趣的可以去读一下原始论文。总之，在不考虑增删操作的情况下，SBF的counter存储所要达到的目标就是只使用O(N) + O(m)位，构建时间为O(m)。通过上面构建的复杂的索引结构，这个目标是达到了！

删除操作相对来说比较好处理，因为它不会导致存储空间的增加。但是也不能坐视不管，因为大量的删除操作会导致本该释放的空间仍然被占用。SBF采取的策略是，单个删除操作只影响相关的counter，整个存储结构并不更新，但经过一系列连续的删除操作后，整个存储结构会被重建。

增加操作稍微麻烦点，因为它意味着原来分配的存储空间不再够用。SBF采取的应对策略有点像我们平时排工作计划时留buffer的做法。我们在安排工作时，如果一件事估计需要10天才能做完，我们写计划时不会写成刚好10天，因为事态的发展有太多动态变化的因素。我们会在计划里给自己留一点buffer，将10天的工作写成12天。

SBF处理增加操作时也采取相似的策略，它给原本只需要N位的基本位串增加єm（є > 0，m为counter个数）位的buffer，以应对将来可能出现的增加操作。SBF将这єm位buffer插入到m个counter之间，每1/є个counter增加1位buffer。当某个counter需要更多位数时，它就找离自己最近的buffer位。如果找到的buffer位就在自己的尾部，就直接用掉它；如果隔了一个或几个counter，它就将隔的这几个counter往后“推”，然后使用腾出来的buffer位。最后，counter移动之后，别忘了索引结构也需要更新。

到此为止，SBF的基本结构就介绍完毕。回顾一下，SBF是一种扩展版的counting bloom filter（CBF），它不仅支持membership query，还支持元素在multi-set中的出现频率查询。实际上，前者只是后者的一种特例，membership query无非是元素出现频率为1的查询。元素出现频率用k（哈希函数个数）个counter中的最小值来近似表示。这种近似使得一个元素对应的k个counter中，最小的那个比其它的更有价值。基于这个考虑，论文作者又对SBF的构建过程进行了优化，并给出了两种优化算法。

在membership query上，由于SBF和CBF都沿用bloom filter的基本结构，因此很难在membership query上提高查询效率。但在查询元素出现频率（大于1的情况）时，由于SBF采用counter中的最小值来近似表示元素的出现频率，使得各个counter的重要性有所差别，因此CBF将counter一视同仁的做法就有提高的空间。

先来看第一种优化算法Minimal Increase。这种算法的思想比较简单，从它的名字大家也能猜出个大概。它的基本思想是：既然在查询元素出现频率时我们只关心counter的最小值，那在增加元素时我们就只增加最小值。如果有多个counter都是最小值，把它们都增加；如果连续加入r个相同的元素，就把最小值（一个或多个counter）加r，其它counter的值或者维持不变，或者设为最小值加r，看哪一个比较大。这种算法是一种聪明的偷工减料：原来增加一个元素时要增加k（哈希函数个数）个counter，现在只需要增加最小值。而counter的增加次数一旦减少，就意味着hashing时碰撞的次数减少，因此查询元素出现频率时出错的可能性也就随之降低。经论文作者证明，Minimal Increase使查询错误率降低了k倍。

当然，偷工减料不可能只有好处。Minimal Increase最大的弊端就是不支持删除操作。很明显，由于增加元素时增加的counter不确定，因此删除元素时也无从下手。如果将k个counter都减少，就会造成false negative的出现（查询结果表明集合不包含某元素而实际上包含）。由于这个严重的弊端，Minimal Increase的应用前景被大打折扣。

下面我们来看一种既支持增删操作又降低查询错误率的算法Recurring Minimum。这种算法的基本思想是：发现有可能出错的情况，然后将它们单独处理。先解释一下什么是recurring minimum。SBF中如果一个元素对应的k个counter中有一个以上都维持最小值，就称它有recurring minimum（RM）。我们发现没有RM（即single minimum）的元素出现查询错误的概率很高，而有RM的元素错误概率很低。因此这种算法将没有RM的元素单独处理，在主SBF之外又增加了一个辅助的SBF，专门用来存储这类元素。由于这类元素所占比例不会太大，因此辅SBF可以只分配较小的空间，比如主SBF的一半大小。

采用Recurring Minimum增加元素x时，先将x在主SBF对应的k个counter的值增加，然后再判断这k个counter有没有recurring minimum。如果有，就当什么事都没有发生，直接继续；如果没有，就意味着x出错的概率很大，这时我们将x存储在辅SBF上，counter的值设为x在主SBF对应counter的最小值。

删除元素和上面的操作类似，由于主SBF没有受算法的影响，所以不会出现false negative。

在查询一个元素时，先看它在主SBF中有没有recurring minimum。如果有，就返回counter的最小值；否则检查辅SBF中的counter最小值，如果大于0就返回这个值，否则返回主SBF的值。

由于有recurring minimum的情况本来出错概率就很小，而没有recurring minimum的情况又单独处理，也大大降低了出错概率，所以整个算法的错误率得以降低。Recurring Minimum算法的错误率虽然不及Minimum Increase，但比原来的错误率要好很多，可以说是用更多的空间换取了错误率的大幅降低。

 

 

 

 

 

 

 

 

 

 

最后

以上就是高挑画笔为你收集整理的布隆过滤器（Bloom Filter）总结-java版为什么要有布隆过滤器简介java实现Counting Bloom FilterSpectral Bloom Filter的全部内容，希望文章能够帮你解决布隆过滤器（Bloom Filter）总结-java版为什么要有布隆过滤器简介java实现Counting Bloom FilterSpectral Bloom Filter所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。