参考网站：https://www.studytonight.com/operating-system/shortest-job-first

1 概念

最短工作优先调度首先处理突发时间或持续时间最短的过程。

• 这是最大限度地减少等待时间的最佳方法。

• 这在批处理系统中使用。

• 它有两种类型：
  非抢占式Non Pre-emptive
  抢占式Pre-emptive

• 要成功实现它，处理器应事先知道流程的突发时间/持续时间，这实际上并非一直可行。

• 如果所有作业/进程同时可用，此调度算法是最佳的。
  
  

2 非抢占式SJF

2.1 非抢占式SJF的原理

考虑以下进程可用的队列中可供执行，到达时间作为所有和给定的突发时间。

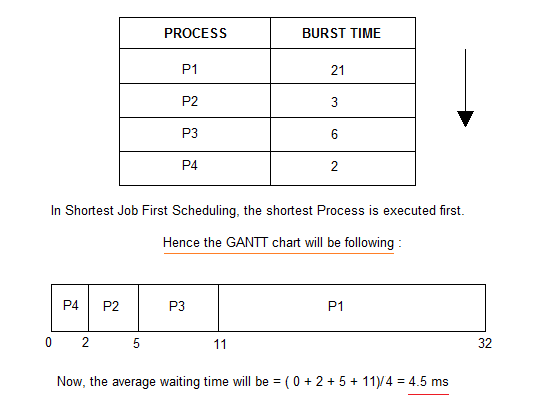
如上图中的GANTT图表所示，首先将执行P4，因为它具有最短的突发时间，然后依次是P2、P3、P1。

我们在上一个笔记中使用了先到先得算法，安排了相同的一组进程，并得到了平均等待时间，而使用SJF时，平均等待时间也是一样的道理。

2.2 非抢占式SJF的缺点

如果进程到达时间不同，这意味着所有进程在准备队列中都不可用，并且某一些作业在一段时间后到达。

在这种情况下，有时具有短突发时间的进程必须等待当前进程的执行完成，因为在非抢占式的SJF中，在持续时间较短的进程到达时，现有作业、进程的执行不会停止以首先执行短期作业。

这导致了Starvation饥饿的问题，在这个问题中，较短的进程必须等待很长时间才能执行当前的较长进程。如果较短的工作持续出现，则会发生这种情况，但是可以使用aging老化的概念来解决。

3 抢占式SJF

在抢先式最短作业优先调度中，作业在到达时会进入就绪队列，但随着突发时间较短的进程到达，现有进程将被抢占或从执行中删除，较短的作业将首先执行。

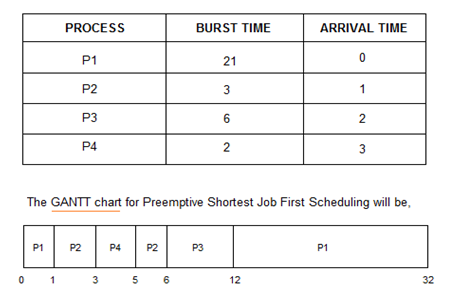
平均等待时间为：((5-3)+(6-2)+(12-1))/4=8.75

抢占式最短作业优先调度的平均等待时间小于非抢占式SJF调度和FCFS调度。

如您在上面的GANTT图表中所见，由于P1首先到达，因此它的执行立即开始，但是在1 ms之后，进程P2到达的突发时间为3 ms，小于P1的突发时间，
因此，将抢占过程P1（完成1 ms，还剩20 ms）并执行过程P2。

随着P2的执行，在1 ms之后，P3到达，但是它的突发时间大于P2的突发时间，因此P2的执行继续。但是再过一毫秒，P4以2 ms的突发时间到达，结果P2（完成2 ms，剩下的1 ms）被抢占并执行P4。

P4完成后，将启动过程P2并完成，然后将执行P2，最后执行P1。

抢占式SJF也称为最短剩余时间优先，因为在任何给定时间点，最先执行剩余时间最短的作业。

4 实现SJF

在下面的程序中，我们将所有作业的到达时间视为0。另外，在程序中，我们将根据所有作业的突发时间对所有作业进行排序，然后像在FCFS调度程序中一样，一一执行它们。

// c++ program to implement Shortest Job first

#include<bits/stdc++.h>

using namespace std;
 
struct Process
{
   int pid;     // process ID
   int bt;      // burst Time
};
 
/* 
    this function is used for sorting all
    processes in increasing order of burst time
*/
bool comparison(Process a, Process b)
{
    return (a.bt < b.bt);
}
 
// function to find the waiting time for all processes
void findWaitingTime(Process proc[], int n, int wt[])
{
    // waiting time for first process is 0
    wt[0] = 0;
 
    // calculating waiting time
    for (int i = 1; i < n ; i++)
    {
        wt[i] = proc[i-1].bt + wt[i-1] ;
    }
}
 
// function to calculate turn around time
void findTurnAroundTime(Process proc[], int n, int wt[], int tat[])
{
    // calculating turnaround time by adding bt[i] + wt[i]
    for (int i = 0; i < n ; i++)
    {
        tat[i] = proc[i].bt + wt[i];
    }
}
 
// function to calculate average time
void findAverageTime(Process proc[], int n)
{
    int wt[n], tat[n], total_wt = 0, total_tat = 0;
 
    // function to find waiting time of all processes
    findWaitingTime(proc, n, wt);
 
    // function to find turn around time for all processes
    findTurnAroundTime(proc, n, wt, tat);
 
    // display processes along with all details
    cout << "nProcesses "<< " Burst time "
         << " Waiting time " << " Turn around timen";
 
    // calculate total waiting time and total turn around time
    for (int i = 0; i < n; i++)
    {
        total_wt = total_wt + wt[i];
        total_tat = total_tat + tat[i];
        cout << " " << proc[i].pid << "tt"
             << proc[i].bt << "t " << wt[i]
             << "tt " << tat[i] <<endl;
    }
 
    cout << "Average waiting time = "
         << (float)total_wt / (float)n;
    cout << "nAverage turn around time = "
         << (float)total_tat / (float)n;
}
 
// main function
int main()
{
    Process proc[] = {{1, 21}, {2, 3}, {3, 6}, {4, 2}};
    int n = sizeof proc / sizeof proc[0];
 
    // sorting processes by burst time.
    sort(proc, proc + n, comparison);
 
    cout << "Order in which process gets executedn";
    for (int i = 0 ; i < n; i++)
    {
        cout << proc[i].pid <<" ";
    }
 
    findAverageTime(proc, n);
    
    return 0;
}

output:

Order in which process gets executed
4 2 3 1 
Processes  Burst time  Waiting time  Turn around time
 4		2	 0		 2
 2		3	 2		 5
 3		6	 5		 11
 1		21	 11		 32
Average waiting time = 4.5
Average turn around time = 12.5

最后

以上就是健忘铅笔为你收集整理的[学习笔记]操作系统(四)最短工作优先1 概念2 非抢占式SJF3 抢占式SJF4 实现SJF的全部内容，希望文章能够帮你解决[学习笔记]操作系统(四)最短工作优先1 概念2 非抢占式SJF3 抢占式SJF4 实现SJF所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。