快速排序算法及其变体快速选择算法详解

       快速排序算法在实际实际生产应用中使用非常多，比如java类库中Arrays类中的sort()方法，以及Collections类中的sort()方法，其一个是对数组进行排序，一个是对集合进行排序。不过这里需要说明的是，在Arrays.sort()和Collections.sort()方法底层实现中不仅采用了快速排序算法，也采用了归并排序算法，因为快速排序算法相对于归并排序算法而言，其对比较（compareTo()）方法的调用的开销比归并排序要大，而对于对象类型，其主要是依赖于compareTo()方法进行比较，而对于基本数据类型，其主要是依赖于基本数据类型的数值比较，因而快速排序算法适用于基本数据类型的排序，而归并排序算法则适用于对象类型的排序。java类库中的Arrays.sort()和Collections.sort()利用多态对传入数组或集合的具体类型来判断是使用快速排序算法还是快速选择算法。

       快速排序算法的核心思想其实是一个通过递归不断选取枢纽元的过程，每次选取枢纽元之后，在枢纽元左边的元素都将比枢纽元要小，在枢纽元右边的元素都将比枢纽元要大，比如下图所示的一个集合：

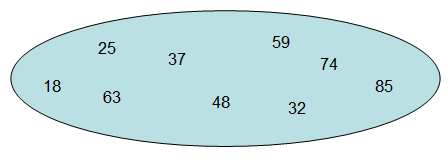
我们选取48作为枢纽元，那么经过一次递归后该集合将被48分割，分割后的集合如下图所示：

从图中可以形象的看出，分割一次之后枢纽元左边的部分的值都比枢纽元要小，枢纽元右边的值都比枢纽元要大。自此，我们可以将枢纽元左边的元素和右边的元素分别看作一个集合，然后对两个集合分别递归的选取枢纽元并进行分割，最终我们的原数组将得到排序。

       根据上边的分析，快速排序算法的核心思想是不断地选取枢纽元，并对原集合进行分割，那么这里如何选取枢纽元，并且每次递归时如何通过枢纽元进行分割呢？首先我们来解决第一个问题，假设原集合元素的下表是从left到right，我们如果选取下标为left + 1的元素为枢纽元，并且要求对集合进行升序排序，那么当我们的原集合本来就是一个降序排序的集合的时候，集合中最小的元素将需要通过不断的换位操作从最右边移动到最左边，由于要进行N - 2次，因而时间复杂度将达到O(N^2)；同理，如果枢纽元靠近下标right，其也不是一个好的选择；一般的，我们都是将枢纽元选择为集合的中间元素。对于第二个问题，由于我们只要求枢纽元左边的元素比枢纽元要小，枢纽元右边的元素比枢纽元要大即可，那么分割思路可以分为三步（假设集合为arr，下标从left到right）：①将集合最左边的元素、中间的元素和最右边的元素进行对比，然后将其中最小的值放在最左边，最大的值放在中间，中等值得元素放在最右边（也即中间元pivot放在最右边）；②声明变量i、j，分别指向最左边的元素的右边一位和最右边的元素的左边一位，将arr[i]和pivot进行比较，如果arr[i]小于pivot，那么就让i自增，同理，将arr[j]与pivot进行比较，如果arr[j]大于pivot时让j自减。此时将出现两种情况：a.i<j，此时arr[i] < pivot，arr[j] > pivot，由于i和j中间部分的元素还未与中间元进行比较，处理方法是将i和j所指向的元素值进行互换，继续第二步；b.i > j，此时arr[i] < pivot，arr[j] > pivot，但是i和j中间部分的元素已经与中间元比较完全，说明i左边的元素都比中间元小，i右边的元素都比中间元大（除中间元外），此时可以进入最后一步；③将中间元（在集合最右边）与下标为i的元素进行互换位置。假设我们现在有一个数组arr = {5, 7, 4, 2, 9, 6, 3, 8, 1};。那么具体的转换步骤如下图所示：

初始位置如上图所示，接着要选取中间元，这里中间元下标为(0 + 9) / 2 = 4，按照步骤①将5，9，1进行比较，并交换位置：

在步骤②中首先声明变量i和j分别指向7和8：

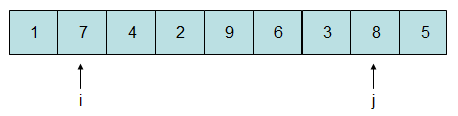
由于7比5大，故i停在此处，而8比5大，将j自减一位：

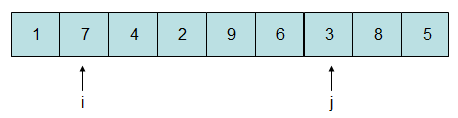
此时由于j所指向的元素值比5要小，j停在此处，由于i比j要小，故将i和j所指向的元素进行互换：

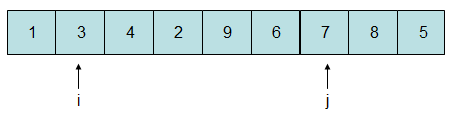
此时3比5小，7比5大，i自增一位，j自减一位：

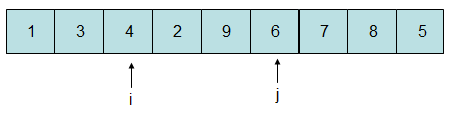
此时4比5小，6比5大，i自增一位，j自减一位：

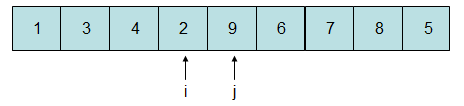
此时2比5小，9比5大，i自增一位，j自减一位：

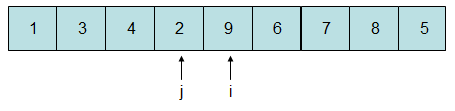
由于9比5大，故i停在此处，2比5小，故j也停在此处，并且由于i比j大，因而步骤②结束，进入步骤③，将i所指向的元素与中间元位置互换：

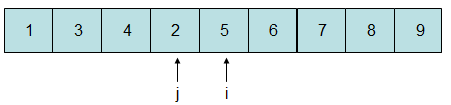
此时，中间元5（也即i所指向的位置）左边的元素都比中间元要小，右边的元素则是大于等于中间元的。此时，我们就达到了通过中间元对集合进行分割的目的。

       这里需要说明的是，当我们要进行排序的集合较小（如大小为20以内）时，快速排序算法没有插入排序算法快（具体原因请查看相关文献），因而对于小集合我们将通过插入排序算法对其排序，具体的代码如下：

public class Sort {
  public static <AnyType extends Comparable<? super AnyType>> void quickSort(AnyType[] arr) {
    quickSort(arr, 0, arr.length - 1);
  }

  private static <AnyType extends Comparable<? super AnyType>> void quickSort(AnyType[] arr, int left, int right) {
    if (left + LENGTH_DIFF <= right) {

      AnyType pivot = medium(arr, left, right);

      int i = left, j = right;
      while (true) {
        while (arr[++i].compareTo(pivot) < 0);
        while (arr[--j].compareTo(pivot) > 0);

        if (i < j) {
          swapReferences(arr, i, j);
        } else {
          break;
        }
      }

      swapReferences(arr, i, right);
      quickSort(arr, left, i - 1);
      quickSort(arr, i + 1, right);
    } else {
      insertionSort(arr, left, right);
    }
  }

  private static <AnyType extends Comparable<? super AnyType>> AnyType medium(AnyType[] arr, int left,
      int right) {
    int center = (left + right) / 2;
    if (arr[center].compareTo(arr[left]) < 0) {
      swapReferences(arr, center, left);
    }
    if (arr[left].compareTo(arr[right]) > 0) {
      swapReferences(arr, left, right);
    }
    if (arr[center].compareTo(arr[right]) < 0) {
      swapReferences(arr, center, right);
    }

    return arr[right];
  }

  private static <AnyType extends Comparable<? super AnyType>> void swapReferences(AnyType[] arr, int i, int j) {
    AnyType tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
  }

  private static <AnyType extends Comparable<? super AnyType>> void insertionSort(AnyType[] a, int left, int right) {
    int j;  // 记录第一个比tmp小的元素的后边一位的位置

    for (int p = left; p <= right; p++) {
      AnyType tmp = a[p];
      for (j = p; j > left && tmp.compareTo(a[j - 1]) < 0; j--) {
        a[j] = a[j - 1];
      }
      a[j] = tmp;
    }
  }

  private final static int LENGTH_DIFF = 20;
}

       快速选择问题指的是获取一个集合中前k大（或小）的元素的集合。快速选择算法则是快速排序算法的一种变体，其思路和快速排序算法非常类似，在快速排序算法每次递归之后，中间元左边的元素都比中间元要大，中间元右边的元素都比中间元要小，由于中间元的下标为i，那么如果i小于k - 1的时候，那么i和i左边的元素都属于要求解的集合的元素，我们只需要对i右边的集合递归调用快速选择算法即可；如果i大于k - 1，那么前k大的集合肯定是i左边集合的子集，我们只需对i左边的集合递归调用快速选择算法即可；如果i等于k - 1，说明i所指的元素及其左边集合的元素正好是前k大的元素，那么递归调用可以终止。快速选择算法的实现例程和快速排序非常相似，只是在每次递归之后对下次递归集合的选取上有所不同，具体代码如下：

public class QuickSelect {
  private final static int LENGTH_DIFF = 20;
  public static <AnyType extends Comparable<? super AnyType>> void quickSelect(AnyType[] a, int left, int right, int k) {
    if (left + LENGTH_DIFF <= right) {
      AnyType pivot = medium(a, left, right);

      int i = left, j = right - 1;
      while (true) {
        while (a[++i].compareTo(pivot) < 0);
        while (a[--j].compareTo(pivot) > 0);

        if (i < j) {
          swapReferences(a, i, j);
        } else {
          break;
        }
      }

      swapReferences(a, i, right - 1);

      if (k <= i) {
        quickSelect(a, left, i - 1, k);
      } else if (k > i + 1) {
        quickSelect(a, i + 1, right, k);
      }
    } else {
      insertionSort(a, left, right);
    }
  }

  private static <AnyType extends Comparable<? super AnyType>> AnyType medium(AnyType[] arr, int left,
      int right) {
    int center = (left + right) / 2;
    if (arr[center].compareTo(arr[left]) < 0) {
      swapReferences(arr, center, left);
    }
    if (arr[left].compareTo(arr[right]) > 0) {
      swapReferences(arr, left, right);
    }
    if (arr[center].compareTo(arr[right]) < 0) {
      swapReferences(arr, center, right);
    }

    return arr[right];
  }

  private static <AnyType extends Comparable<? super AnyType>> void swapReferences(AnyType[] arr, int i, int j) {
    AnyType tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
  }

  private static <AnyType extends Comparable<? super AnyType>> void insertionSort(AnyType[] a, int left, int right) {
    int j;  // 记录第一个比tmp小的元素的后边一位的位置

    for (int p = left; p <= right; p++) {
      AnyType tmp = a[p];
      for (j = p; j > left && tmp.compareTo(a[j - 1]) < 0; j--) {
        a[j] = a[j - 1];
      }
      a[j] = tmp;
    }
  }
}

       本文详细叙述了快速选择算法的实现思想，分割策略以及每次分割的具体历程，并且简要概述了快速排序算法的变体快速选择算法及其实现例程。