概述
1. 冒泡排序：时间复杂度：O(n^2) , 空间复杂度：O(1)
第一个逐次和后面比，先拍好后边的，最大/最小。
每次拍好之后减少比较次数，后面排好的不用再去比较
nums = [1, 9, 10, 20, 2 ,5 ,9,0]
① 用 1 分别和列表中的每位元素比较，比1大的话就不动[1, 9, 10, 20, 2 ,5 ,9,0]
② 用 9 去分别比较，10比9 大不动[1, 9, 10, 20, 2 ,5 ,9,0]
… 后面大的保持位置
④ 到 20 比2 大换位置[1, 9, 10, 2, 20 ,5 ,9,0]
⑤ 到 20 比5 大换位置[1, 9, 10, 2, 5 ,20 ,9,0]
⑥ 直到[1, 9, 10, 2, 5 , 9, 0, 20]
… n 是已经排好序的，不用每次遍历到尾部
nums = [1, 9, 10, 20, 2 ,5 ,9]
n = 0
while n < len( nums ):
for i in range( 0, len( nums ) - 1 - n): # n是后面排好的个数就不循环了
if nums[i] < nums[i+1]: # 下一个比上一个大就交换位置
nums[i], nums[i+1] = nums[i+1], nums[i]
n += 1
print(nums)
2. 选择排序： O(n^2) , 空间复杂度：O(1)
先排好前面，每次选取最小/最大的放到前面，再从未排序中找最小/最大加到排好的后边。
nums = [1, 9, 10, 20, 2 ,5 ,9,0]
① 用 1 分别和列表中的每位元素比较，比1小的话就交换位置[0, 9, 10, 20, 2 ,5 ,9,1]
② 用 9 去分别比较，比2 大换位置[0, 2, 10, 20, 9 ,5 ,9,0]
然后还会继续往下遍历 2 和 5， 9 ，0比，1<2 换位置[0, 1, 10, 20, 9 ,5 ,9,2]
… n 是已经排好序的，不用每次从头开始去遍历，知道最后一位就停止循环
n = 0
while n < len( nums ):
for i in range( n, len( nums ) - 1 ): # n 开始前面是已经排好的，n是没排好的
if nums[n] > nums[i+1]: # 如果有比自己还小的换值直到自己最小
nums[n], nums[i+1] = nums[i+1], nums[n]
n += 1
print(nums) -- [0, 1, 2, 5, 9, 9, 10, 20]
细讲网址：https://xiaoqi.blog.csdn.net/article/details/109193651
3. 插入排序：时间复杂度为O(n^2)，空间复杂度为O(1)
a = [1, 9, 10, 20, 2 ,5 ,9]， 用后面的和前面的比较
① 用 9 和1比，9>1不变[1, 9, 10, 20, 2 ,5 ,9]
② 用 10 和9比 10 >9 不变[1, 9, 10, 20, 2 ,5 ,9]
… 升序的话后者小就不变
③ 用 20 和2比 20 >2 交换位置[1, 9, 10, 2, 20 ,5 ,9]
④ 2 需要和前面排序好的每一个比较 ，比前面小的换位置，小的在前面
[1, 9, 2, 10, 20 ,5 ,9] - [1, 2, 9, 10, 20 ,5 ,9] 直到 1 < 2 停止
… j 是不断变化的，会每次往前移动一位
a = [1, 9, 10, 20, 2 ,5 ,9,0]
for i in range(1, len(a)): # 没有 i + 1 的情况下不用len(a)-1，因为长度是8索引只能到7
res = a[i] # 第二个数开始
j = i - 1 # 第i前的一个数
while j >= 0 and res < a[j]: # 如果还有前一个和前一个>后面的就换位置
a[j], a[j+1] = a[j+1] , a[j]
j -= 1 # 再去和前一个做比较
res = a[j+1] #因为j上一步减1了所以j+1 回到原位
print(a)
4. 快速排序：时间复杂度为最优O(nlogn)，最坏时间复杂度O(n^2)空间复杂度为O(1)
因为每次将序列切分为2部分，如果切割了n次把元素切割完，序列的长度为m，则2^n=m，所以切割的时间复杂度为log（n),在每次切割的时候都会比较所有的元素，需要n次，所以整体的时间复杂度为O(nlog(n))。
如果每次左边都只有一个元素那就是最坏时间复杂度 O(n^2)
快速排序： 以第一位为基准，大于基准的放到右边，小于基准的放到左边
稳定性：不稳定
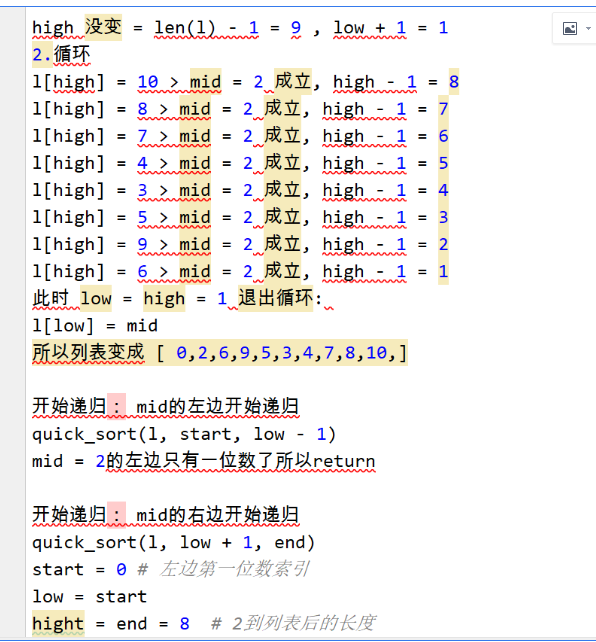
数组 l = [ 2,10,6,9,5,3,4,7,8,0,]
1. 以第一位为基准，大于基准的放到右边，小于基准的放到左边
2. 以l[0] = 2做完为基准，start是0， end是len(l) - 1, low = start, high = end
3. 只要low没有等于high就一直循环，
注意的是在递归之前mid没变化 ，直到最后放到中间位置
当中只要l[high] >= mid ，位置本就在右边是正确的，不动high+1。
当中只要 l[low] < mid，位置本就在左边是正确的，不动low-1。
每次循环l[low] = l[high], l[high] = l[low]
等于mid的数可以放在左边也可以放在右边，所以只有一个 = 号
4. high 没变 = len(l) - 1 ， low + 1 = 1 循环第三步；
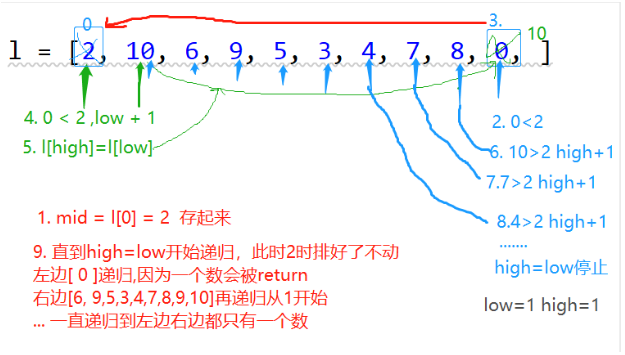
def kuaipai(l, start, end):
low = start
high = end
if high <= 1 or low > high:
return
mid = l[low] # 把第一个数作为基准
# 当low等于high的时候说明已经比较完当前的列表退出
while high > low:
while high > low and l[high] >= mid: #
# 右边的数大于基准说明位置正确留在原位不动, 右边的索引减一
high -= 1
# high < mid 说明需要放到左边去
l[low] = l[high]
while high > low and l[low] < mid: #
# 左边的数小于基准说明位置正确留在原位不动, 左边的索引加一
low += 1
# low > mid 说明需要放到左边去
l[high] = l[low]
# l[low] = l[high], l[high] = l[low] 会有两个一样的值，所以让l[low] = mid，并不会丢失数据
l[low] = mid
kuaipai(l, start, low - 1) # 分好左右之后先排左边
kuaipai(l, low + 1, end) # 排右边
if __name__ == '__main__':
l = []
import random
for i in range(0,11):
l.append( random.randint(1,29) )
kuaipai(l, 0 , len(l) - 1)
print(l)
5. 归并排序：时间复杂度为最优最坏都是O(nlogn)
把列表每次2分，知道只有一个元素，把这些元素按照大小逐渐合并成完整列表
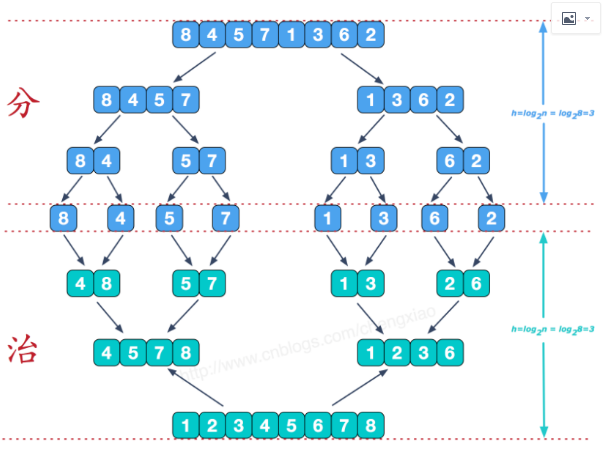
详解看递归分析
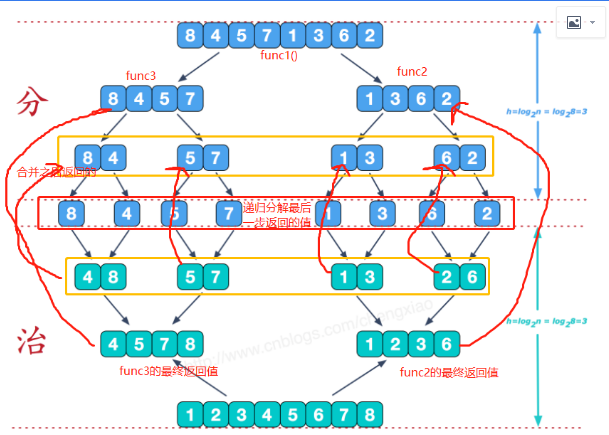
def merge_sort(alist):
n=len(alist)
if n<2:
return alist
mid = n // 2
left_li = merge_sort(alist[0:mid])
right_li = merge_sort(alist[mid:])
# 逐步合并
result = []
left_pointer, right_pointer = 0,0
while left_pointer < len(left_li) and right_pointer <len(right_li):
if left_li[left_pointer] < right_li[right_pointer]:
result.append(left_li[left_pointer])
left_pointer += 1
else:
result.append(right_li[right_pointer])
right_pointer += 1
# 循环结束之后有某个列表中比较大的是剩下的加到result
result += left_li[left_pointer:]
result += right_li[right_pointer:]
return result
if __name__ == '__main__':
l = [8,4,5,7,1,3,6,2 ]
print(merge_sort(l))
最后
以上就是单身枕头为你收集整理的排序算法详解-- 冒泡排序-选择排序-插入排序-快速排序-归并排序的全部内容，希望文章能够帮你解决排序算法详解-- 冒泡排序-选择排序-插入排序-快速排序-归并排序所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复