数据结构算法题/top K问题

66 阅读 0 评论 44 点赞

我是靠谱客的博主心灵美巨人，最近开发中收集的这篇文章主要介绍数据结构算法题/top K问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

问题描述：有N(N>>10000)个整数,求出其中的前K个最大的数。（称作Top k或者Top 10）

问题分析：由于(1)输入的大量数据；(2)只要前K个，对整个输入数据的保存和排序是相当的不可取的。

解决方案1：最小堆

可以利用数据结构的最小堆来处理该问题。最小堆如图所示，对于每个非叶子节点的数值，一定不大于孩子节点的数值。这样可用含有K个节点的最小堆来保存K个目前的最大值(当然根节点是其中的最小数值)。

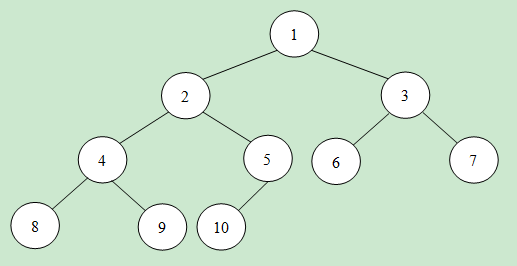
每次有数据输入的时候可以先与根节点比较。若不大于根节点，则舍弃；否则用新数值替换根节点数值。并进行最小堆的调整。

解决方案：

（1）每次对前K个进行建最小堆，不是n个

（2）使用最小堆

原因是：首先选前k个构建最原始的最小堆。然后对于下一个输入的数据，如果不大于根节点就舍弃，否则用新数值替换根节点数值，同时对最小堆进行调整。（对于最小堆里面的k个元素可以理解成目前最大的k个值。）

（3）时间复杂度是nlogk

由于保存了K个数据，调整最小堆的时间复杂度为O(lnK)，因此TOp K算法(问题)时间复杂度为O(nlnK)

代码1使用java自带的堆接口PriorityQueue

import java.util.PriorityQueue;

/**
 * PriorityQueue实现了数据结构堆，通过指定comparator字段来表示小顶堆或大顶堆
 */
public class HeapTopK {
    public int findKthLargest(int[] nums, int k) {
        PriorityQueue<Integer> minQueue = new PriorityQueue<>(k);
        for (int num : nums) {
            if (minQueue.size() < k || num > minQueue.peek())// 堆还不满k个的时候或者堆顶小于下一个要进来的数据时，将该数据插入最小堆
                minQueue.offer(num);
            if (minQueue.size() > k)
                minQueue.poll();
        }
        return minQueue.peek();
    }

    public static void main(String[] args) {
        HeapTopK heapTopK = new HeapTopK();
        int a[] = {1, 5, 6, 2, 4, 10};
        System.out.println(heapTopK.findKthLargest(a, 3));
    }
}

解决方案2：quickselect（借鉴quicksort的思想,因为是top K所以也就是借鉴逆序排序的快排思想）时间复杂度nlogn。

本方法找出第k大的数据，在计算的过程中可以记录top k的数据。quickselect和quicksort使用的相同的计算主元partition的方法。

选取一个基准元素pivot，将数组切分（partition）为两个子数组，比pivot大的扔左子数组，比pivot小的扔右子数组，然后递推地切分子数组。Quick Select不同于Quick Sort的是其没有对每个子数组做切分，而是对目标子数组做切分。其次，Quick Select与Quick Sort一样，是一个不稳定的算法；pivot选取直接影响了算法的好坏，worst case下的时间复杂度达到了O(n2)。

Quick Select的目标是找出第k大元素，所以

若切分后的左子数组的长度 > k，则第k大元素必出现在左子数组中；
若切分后的左子数组的长度 = k-1，则第k大元素为pivot；
若上述两个条件均不满足，则第k大元素必出现在右子数组中

/**
 * Created by liyang54 on 2018/10/14.
 * 选择topK需要逆序排序
 *
 * 下面针对的是调整主元之后的数组
 * 若切分后的左子数组的长度 > k，则第k大元素必出现在左子数组中；
 * 若切分后的左子数组的长度 = k-1，则第k大元素为pivot；
 * 若上述两个条件均不满足，则第k大元素必出现在右子数组中。
 */
public class QuickSelectTopK {
    // quick select to find the kth-largest element，返回第k个元素
    // 递归的
    public int quickSelect(int[] arr, int k, int left, int right) {
        if (left == right) return arr[right];
        int index = partition(arr, left, right);
        if (index - left + 1 > k)
            return quickSelect(arr, k, left, index - 1);
        else if (index - left + 1 == k)
            return arr[index];
        else
            return quickSelect(arr, k - index + left - 1, index + 1, right);
            //k - index + left - 1表示左边（0，index）都不是了，已经去除了index-left+1个了，
            //只需要再剩下的k-(index-left+1)中找即可。
            // （也就是在右边的index+1到right这个区间的找的时候，不是原来的数组A第K个了，是右边新数组的k - index + left - 1）
    }


// 下面的计算主元的方法和快排的是一样的，公用的
// 因为是topk，下面需要的是逆序的
// partition subarray a[left..right] so that a[left..j-1] >= a[j] >= a[j+1..right]
// and return index j
// 逆序排序的partition
    private int partition(int A[],int p,int r){
        int x=A[r];//把每次数组A的最后一个元素作为主元
        int i=p-1;//开始的时候将i 移动到数组的外面
        for(int j=p;j<=r-1;j++){
            if(A[j]>=x){
                i++;
                swap(A, i,j);//p--i是小于等于x的,i+1--j-1是大于等于x的所以要交换下
            }
        }
        swap(A, i+1, r);//把主元放在中间好区分两边的
        return i+1;//返回主元的位置
    }

    private void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

    public static void main(String[] args) {
        QuickSelectTopK quickSelectTopK = new QuickSelectTopK();
        int a[] = {1,36,2,5,7,4,9};
        //下面输出的是第三大的
        System.out.println(quickSelectTopK.quickSelect(a, 3, 0, a.length-1));
    }
}

参考https://www.cnblogs.com/en-heng/p/6336625.html